Fuel consumption
Some facts: In the USA, 28% of all energy consumed is used for transportation. Of this transportation energy, 93% comes from petroleum. Cars and light trucks account for 59% of US transportation use, with the average fuel consumption of cars in the USA being around 23 mpg.
 Hybrid Image: Alexander Chernov, MarkinDetroit
Hybrid Image: Alexander Chernov, MarkinDetroit
US transportation petroleum use is currently at 161% of the total US production of petroleum, so much is imported.
The misrepresentation of fuel consumption by quoting fuel efficiency
 |
Traditionally, fuel consumption figures for vehicles are quoted as miles achievable per gallon or MPG. This term is so commonly used and present in our vernacular that it seems so obvious and natural a measurement. MPG, however, is more accurately a measure of fuel efficiency. |
|
Fuel efficiency is not the most appropriate or intuitive method for measuring fuel consumption. I’ll give some examples later, but the fundamental reason is that we’re trying to measure consumption, and when measuring miles per gallon, the consumption term is on the denominator and so this results in a reciprocal proportional representation. The human mind is much better at dealing with linear relationships (especially when dealing with comparison situations). |
 |
 |
It might sound like a small difference, but a much more appropriate/understandable measure for fuel consumption should be gallons per mile. This inverse is the way things are measured in other countries in the World. Where the metric system is common place, fuel consumption is typically measured by L/100 Km (Litres per 100 Km). Litres per 100 Km is used instead of Litres per Km, just to make the numbers a little more manageable with less decimals. |
Fuel consumption is a better measure of a vehicles performance because it is a linear relationship with the fuel used, as opposed to fuel economy which has an inherent reciprocal distortion.
Ask yourself the question, would you rather know how far you could travel on a gallon of gas, or how much gas you are going to use on your trip?
Gallons per Mile
The graph below shows the relationship between MPG and the number of gallons needed to drive 1,000 miles. The reciprocal relationship is clearly visible. (I've used 1,000 miles, just to make the numbers bigger and less decimals. It's also a good estimate to the number of miles that average person will drive in a month).
If your car does 20 MPG, then to travel 1,000 miles you will need 50 gallons of fuel.
If your car does 25 MPG, then to travel 1,000 miles you will need 40 gallons of fuel.
If your car does 100 MPG, then to travel 1,000 miles you will need 10 gallons of fuel.
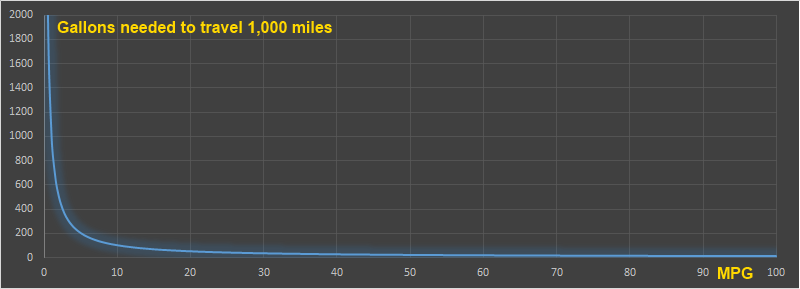
Because of this non-linear relationship, equal increases in MPG improvements do not equate to equal improvements in gas savings.
A 5 mpg improvement in fuel efficiency of a vehicle from 10 mpg to 15 mpg results in a savings of 33.33 gallons over the course of 1,000 miles. Quite an improvement. Especially now that gas is close to $4.00/gallon.
A 5 mpg improvement for a vehicle that already does 30 mpg results in a much smaller savings of just 4.76 gallons over the same 1,000 miles.
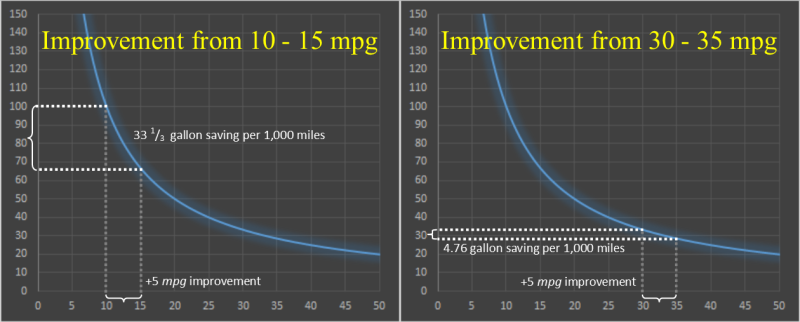
Let's be clear, a car with a higher fuel efficiency (higher mpg), will always use less fuel than one with a lower fuel efficiency; you should always go for the most fuel efficient car you can, but what I am showing is that similar linear increases in mpg efficiency make different improvements in fuel savings.
The more fuel inefficient a vehicle is, the bigger the improvement in fuel savings will be for a small improvement in efficiency. Replacing a car with a fuel efficiency of 10 mpg with one with a fuel efficiency of 11 mpg will save more fuel than replacing a car with a rate of 30 mpg with one with a rate of 41 mpg!
If your family really needs a huge full-size monster of a vehicle, exchanging it with even a slightly more efficient equivalent monster (possibly a hybrid?) could make a substantial difference to your monthly fuel costs. Conversely, changing an already highly efficient car into a hyper efficient car is not going to make a big change in your monthly fuel bills, even with a, potentially, large step up in efficiency.
Family cars
 |
This non-linear relationship also means that averages are harder to comprehend. For example, if a family has two cars; an SUV rated 16 mpg and a compact car rated 35 mpg, if both cars are driven the same distance each year, less fuel would be used by the family if they replaced both cars with a pair of cars rated 22 mpg each! If fuel consumption rates were measured in gallons per mile, comparisons and improvements would be much easier to comprehend, and could be simply added an subtracted. |
An SUV with an efficiency of 16 mpg consumes 62.50 gallons per 1,000 miles.
A compact car with an efficiency of 35 mpg consumes 28.57 gallons per 1,000 miles.
Total for both cars is 62.50 + 28.57 = 91.07 gallons per 1,000 miles.
91.07 ÷ 2 = 45.54 gallons per 1,000 miles (per car).
A car with efficiency of 22 mpg has a consumption of 45.45 gallons per 1,000 miles (which is less).
How much does that extra speed cost you?
 Image: ChrisM70 Image: ChrisM70 |
Fuel efficiency varies with speed: Aerodynamic drag increases proportional to the speed squared. There is rolling resistance from the tires, and transmission losses. The internal combustion engine is more efficient at different engine speeds, and cars have gear boxes to convert the torque generated by the engine to drive the wheels at appropriate speeds for the conditions. Drive a car too slow, and in a lower gear you’re wasting the efficiency of the engine, and the fixed parasitic losses associated with the cars mechanical systems rob your efficiency. Drive a car too fast and you’re burning additional energy for the luxury of pushing through the air at a faster speed. But at what costs? Have you ever wondered about the ‘miles per gallon per mile per hour’ curve? (I guess you could call this velocity specific fuel consumption). |
Fuel consumption with speed
|
Obviously, every make of car has different profile curves, but here is some data based on average information obtained from US Department of Energy statistics. Graphed out (with speed on the x-axis and fuel efficiency on the y-axis) we can see how, in this case, the highest efficiency of the vehicle is obtained around 50-55 mph. Faster than this, aerodynamic drag becomes more important, and below this speed, gearing and other losses don’t make the most efficient use of the engines output. If you were going to drive a one particular fixed speed to maximise your range then, in this particular car, it would be most advantageous to travel at a speed of 50-55 mph (we're ignoring here any effect of gradient or wind). |
 |
|
This can be seen clearly on the graph on the right which shows a fictitious trip of 200 miles. I've used an estimate of $4.00/gallon to set some context but, of course, when comparing the realtive values, the price of gas is not important. We can see that the graph has a minimum at the 50-55 mph region at just less than $25. The curve is pretty flat from the region 30 mph up to 60 mph, rising slightly in the middle (probably because at 40 mph the speed is still too slow to efficiently engage the top long gear, so the engine is revving higher than its optimal peak efficiency). Above 60 mph, even the top gearing and efficiency of the engine starts to battle aerodynamic drag, and the engine has to generate more power. |
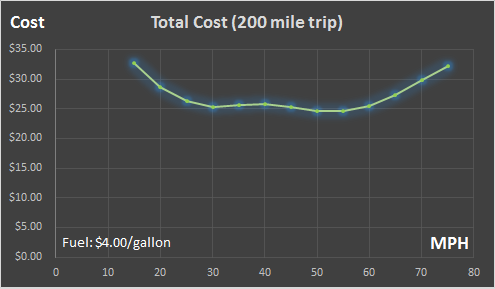 |
|
When we travel faster we cover distance in a shorter time, but this comes at the penalty of higher fuel consumption. To the right is a graph of the fuel cost based on time, when traveling at constant speed. (This graph is just the fuel consumption rate gallons/hour multiplied by the cost of fuel, in this case, $4.00). The graph goes upwards and to the right; the faster you travel the faster the fuel burn rate (this would be the case even if the fuel efficiency rate were constant with speed. The fact that fuel efficiency changes with speed adjust the gradient of this curve). |
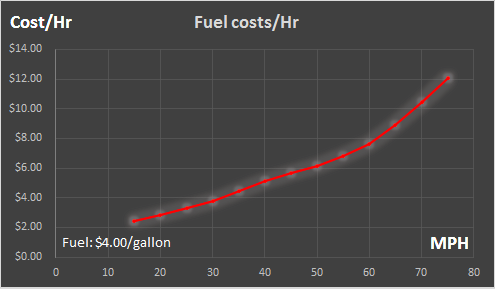 |
How much is your time worth?
|
We know that the most efficient speed to travel is 55 mph. What happens if we travel faster? As we have seen, our consumption rate gets higher at higher speed. To the right is the delta (difference) between the hourly rate of traveling at 55 mph (the most efficient speed) compared to other speeds. If you elect to travel at 60 mph, this will cost you an additional $0.85 per hour of travel. If you travel at 65 mph, this works out at $2.11 per hour. At 70 mph, this increases to $3.66 per hour, and finally, at 75 mph, the additional cost is $5.31 per hour. (I'm ignoring completely, the concept of travelling slower than 55 mph. This takes longer and is more inefficient. A lose-lose situation!) |
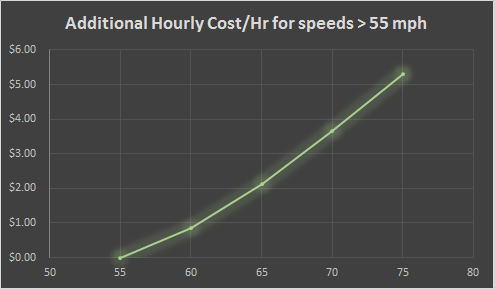 |
 |
Based on the data for this car, if you were hiring a dog sitter to look after your pet and they charged by the hour and you were driving back to collect the pet then, if the sitter charged more than $5.31/hour, it would be in your interest to drive faster (driving at 75 mph instead of 55 mph) to get there sooner as the additional cost you’d spend on fuel/per hour would compensate for the shorter fee you would be paying the sitter. All of this, of course, does not take into account the value of your own time, the additional wear and tear on the vehicle and the chance that you might get a speeding ticket! Also remember that your car will have different performance figures than those I used here for illustration. Please don't send me your pet sitter bills! |
Driving to a Gas Station
 Image derived from: chapstickaddict
Image derived from: chapstickaddict
|
It’s human nature to want to get a good deal. We hate paying a higher price for a commodity item like gas. If the gas station directly in front of you is selling gas at $4.00 a gallon, and you know that down the road the gas only $3.95 a gallon, is it worth driving the extra distance? If the alternate gas station is on your desired route, then sure, it’s a no brainer. But if not, you have to factor in that you have to drive there and back. The function for whether to make this detour also depends on the amount of gas you intend to buy (The more free space you have in your tank the more you can capitalize on the cheaper gas, and the further out of your way you would drive to get this benefit). |
Sample Calculation
|
Using the approximation that in city driving your car achieves 25 MPG, and your tank can take an additional 10 gallons of fuel to fill up then, for every penny that gas is cheaper at the further station, you will save a dime by filling up. To get to this station you will need to drive (there and back), so at 25 MPG, every mile away the station is, it will cost you approximately $0.32 to get there (using a base price of $4.00/gallon). The break-even threshold for this scenario is therefore around $0.03/gallon cheaper per mile away from the near station. A smaller price difference than this and it is better to suck it up and pay the premium price. A larger price difference, and it is in your fiscal best interests to drive the further distance. |
 |
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.

