Compound Interest
 |
Interest is a powerful thing. When you borrow money, you pay interest. When you lend money, you earn interest. Interest is typically measured as percentage of the principal, and to correctly define it you also need to specify the period over which this is calculated. Interest compounds. Starting with the principal, after interest is calculated and paid, it is added to the original amount make a new larger principal. This larger principal now garners slightly more interest, and so on … In the words of Ben Franklin: “The money that money earns, earns money” |
I've written about this a little in the past in my artricle about How much do you spend in your life on coffee?
Albert Einstein
“The most powerful force in the universe is compound interest” – Albert Einstein
As an illustration of how powerful a force this is, take this little example: Imagine you made a 1% improvement in your life each day for an entire year. After 365 days, your skills will have improved and compounded to almost a 38x improvement from your starting level.
Conversely, a 1% decline everyday (99%) will result, after 365 days, in a skill level of just 0.0255 of your starting level. Quite a phenomenal deterioration.
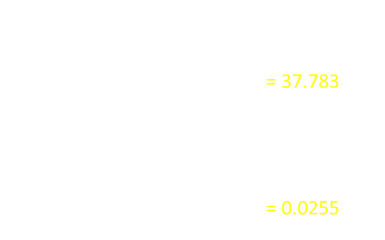
I hope you listen to your teachers and parents when they tell you the value of practising every day!
The limit of compounding, and the period of the interest
|
Imagine you have $1,000 in the bank, and they agree to pay you 20% interest per year. If they paid this annually, at the end of the first year you would have $1,200. At the end of the second year you would have $1,440. At the end of the third year $1,728 … What if, instead of giving you 20% for the year, they paid you half the interest twice a year? (10% every six months) After the first six months you’d have $1,100 and after the first year you’d have $1,210. This is $10 more than settling just once a year. Taking this further, how about if the interests was paid 5% every quarter? After the first year you’d have $1,215.51 (a delta of $15.51 over the yearly compound). If we continue reducing and reducing the compounding period, will we continue to make more and more money? |
 |
|
NO! As we reduce the time slices to be smaller and smaller, the benefit of the more rapid compounding gets smaller and smaller. To the left you can see a table of earnings in this example. Various periods of compounding are shown in the table. For each row, the number periods and the interest rate in each period are shown (20%/n), followed by the total at the end of one year and the delta from the simple yearly compounding. The amount of money earned in a year is given by the following formula: 
|
 |
The earning difference between compounding weekly and hourly (using our example figures) is less than two quarters. The difference between compounding every second, instead of every minute, is less the five thousandths of a penny! Mathematicians reading this will realize the the limit to the earnings are defined by Eulers exponential function e |
Here is a graph showing ten years of this compounding with different periods:

Multiplication
To get the final total, we take the product of all the intermediate calculations and multiply this by the principal. For example, if the interest rate was R and there were four periods, the calculation is as follows:
There are some interesting consequences that occur because of the way the percentages compound.
Investment Strategies
A 'friend' offers a choice of two investments. Their percentage growth rates over four years are shown below.
Which is a better investment?
- Year 1: +10%, Year 2: -10%, Year 3: +10%, Year 4: -10%
- Year 1: +25%, Year 2: -25%, Year 3: +25%, Year 4: -25%
Both vacillate symmetrically, gaining one year, then losing the next. At first glance it would appear that there is no difference between these two investments, and you could be forgiven for saying that both are equivalent and totally neutral in earning potential.
However, the truth is that these are both bad investments, and investment #2 is far worse that investment #1.
Let's take a look why. Here are the expansions for the two investments:
For every $100 placed in investment #1, you would see $98.01 at the end of four years. For every $100 placed in investment #2, you would see just $87.89 at the end of four years. It's easy to see that any investment that swings backwards and forwards by symmetric gains and losses will always lose money. Let x represent the interest rate:
As x2 must always be positive, then (1-x2) must always be less than 1.0, and so the Rate will always be less than 1.0
Comparing Investments
What happens if the investments are more complex? How would you compare the following seven year investments? Which of these will produce the best return? A, B, C, D, E or F?
|
Have a guess. It doesn't matter if you are right or wrong, the point is, it's hard to tell just by looking at the numbers. To calculate the return, as before, we need to multiply out the percentages. Some of these investments have big swings, others are more gentle. |
The return on investment A after seven years can be determined:
(It should also be brutally obvious that if you lose 100% of your capital at any stage then is is game over)
Results
Here is a plot of the outputs of these investments against time. All start normalised at 1.0 and them fluctuate up and down based on the percentages. To calculate the revenue at any time the principal can be multiplied by the normalised value.
After seven years, it is investment F that finishes with the highest return (with just over 5.25% compounded growth). Only one other investment (Investment D) broke even and finished at higher value than the starting value of 1.

"Average" interest rate
Trying to compare different investments with varying interest rates is hard because of the complication of the multiplication and powers.
If only there was some way to 'average' the interest rates over the investment period …
... we'll, there is!
 |
Average The mathematical word for 'average' is the word 'mean', but there are many different kinds of mean depending on what you are trying to measure! If you were grading exam papers, you might want to calculate the arithmetic mean. To do this, you sum up the scores for all the papers, and divide by the total number of papers (sort of like evenly distributing the points amongst all the papers, so that every paper gets the same number of points). This is typically what most people think of when they talk about the 'average'. This is the arithmetic mean. You might, instead, consider that the 'average' exam paper is the one that has the score that most people achieve. (The 'average' response to a question could be interpreted as the answer that the most people people think). Mathematicians call this average the Mode. Different again, is something called the Median. To calculate this you arrange all the answers in order and pick the middle value. A simple way to think of this is that are are "as many answers higher than this as there are lower than this". By definition, you have selected the answer that is in the middle with the median. All of these are great averages, and each has uses, but for our compounded interest they will not help. We need to come up with an average (mean) that we can use to derive the answer using just the mean value and the time period. If the interest rate were constant that would be easy. We could just say "an interest rate of 5.25% per year for seven years" and everything would be determinable. We need to come up with a different kind of mean. |
Geometric Mean
|
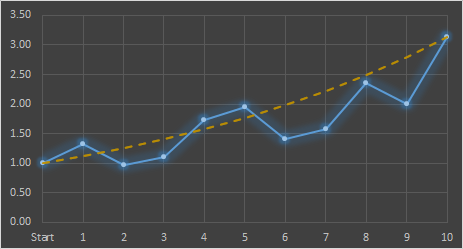
The Geometric Mean comes to our rescue. To calculate the geometric mean, we multiply all n individual percentages together, then take the nth root of this product. By multiplying all the percentages together we get the final compounded value, then, by taking the applicable root of this value we distribute this appropriately over the periods 'equally'. This geometric mean reduces the series of individual interests into one 'average' fixed number that we can simply use in the simple fixed-rate compounding formula. As an example, look at the table to the right showing ten years with differing levels of yearly interest: The geometric mean is calculated by multiplying all the interests together (This product results in a value of 3.13316), then by taking the 10th root (this is spread over 10 years) we get the geometric mean. An easy way to think of this is imagine what would be the same ('average') interest value that we could apply to all ten years to generate this answer. For this example, the answer is 12.1% |
|
Over 10 years, the total growth of the portfolio is 313%, and this could be achieved by applying a constant 12.1% interest over the 10 years. In the graph below, the blue line shows the cumulative compounded interest, and the orange dotted line shows the curve of constant 12.1% interest. By definition, the two curves meet at the beginning and end of the period.
|
|
The rule of 72
|
As interest compounds, things get bigger. Often it’s useful to know how long it will be until the original principal has doubled. Using what we’ve learned it’s possible to derive a formula to calculate the time period, but there is a very easy to remember rule of thumb approximation and it’s called The Rule of 72 It goes like this. Let’s say you have an investment with an annual interest rate of 6%. How long would it take for your initial investment to double in value? To estimate this, simply divide 72 by 6. The answer = 12. So, with an interest rate of 6%, it will take approx. a dozen years to double your initial investment. At 4% interest, it would take 72/4 = 18 years to double (approx). The rule also works the other way around: What interest rate would you need to receive to double your investment in 5 years? Answer, approx. 14.4% |
 |
Why does the Rule of 72 work?
 |
Recall that the Value at any point is the Principal multiplied by the compound of the interest rate:
The investment has doubled when the Value is twice the principal. |
Taking natural logs of both sides then, by using the Taylor Series approximation for the logarithmic function, we can show that (for small values of R), that ln(1+R) ≈ R

Finally, converting R from a decimal into an, easier to use, percentage requires multiplying by 100. Our estimate shows that it should be 69.31/percentage rate, so why is 72 used? The simple answer is that 72 has many factors (1,2,3,4,6,8,9,12 …), and since it is meant to be a rule of thumb calculation, using 72 makes it very easy to get quick approximations.
How good is the approximation?
|
To the left are a series of example interests percentages and the calculations for how long it will take at this rate to double the investment. The middle column gives the true number of years, and the right column gives the answer as estimated by the Rule of 72. The estimates are pretty good. If you wanted a more accurate approximation, you could replace the 72 by 69.3 (This will make the small percentage answers much more accurate, but as the percentages increase the simple Taylor Series approximation continues to strain). A next level of sophistication is to take more terms of the Taylor Series approximation and use a better approximation of ln(1+R) e.g. as R-R2/2 These techniques might have been useful when calculations were performed by hand, or with log tabs or slide rulers, but these days, if you want a more accurate answer than the approximation the rule of 72 gives, I'd use a calculator or computer!
|
The restaurant at the end of the Universe
If you need any more proof of the power of compounding interest, you must read the second book in the comic series "The Hitchiker's Guide to the Galaxy", which describes Milliways, the restaurant at the end of the Universe, from which the book gets its title.
 |
All you have to do is deposit one penny in a savings account in your own era, and when you arrive at the End of Time the operation of compound interest means that the fabulous cost of your meal has been paid for. This, many claim, is not merely impossible but clearly insane, which is why the advertising executives of the star system of Bastablon came up with this slogan: "If you've done six impossible things this morning, why not round it off with breakfast at Milliways, the Restaurant at the End of the Universe?" – Douglas Adams |
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.