
	Advertisment

Pleated Sauce Cups

Recently, a meme has been floating around the social webs. It concerns those pleated paper sauce cups found in a variety of dining establishments. Here’s one that appeared on my facebook page today.

It seems that most of us do not know that it’s possible to relax the pleats of these containers in order to store more ketchup (or mayonnaise, mustard, BBQ sauce, tartar sauce …)

The posting I received had the comment:

“If only I’d known that I could store twice the amount of ketchup this way, then I’d not have been wasting two containers all this time!”

But hang on a minute? Is this true? Can you really store twice the volume of ketchup this way? And, more interestingly, what is the optimal angle to relax your pleats to? Time for some math …

Frustum

First, we need a way to work out the volume of ketchup in the cup in its varying configurations.

If you look closely you will see the shape of the cup is that of a truncated cone. Mathematicians call this shape a Frustum.

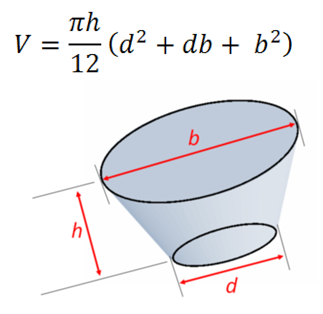The formula for the volume of conical frustum is shown to the left^*

For those interested in rocket science, frustum shapes occur quite regularly as fairings between locations of different diameters on cylindrical structures. Who can forget the classic shape of the beautiful Saturn V rocket?

^*Assuming the face of the cut tip is parallel to the cone base, and both are perpendicular to the axis of the cone!

Ketchup and rockets!

Not all cups are created equal

Pleated sauce cups are manufactured in a variety of sizes. A quick visit to my local establishment secured one that I could measure.

The one I obtained had the following dimensions:

h = 42mm, d = 53mm, b = 75mm

When the cup is deformed, and the pleats relaxed, the cup flattens. The base of the cup remains the same diameter, but the top of the cup expands.

Using a little trigonometry, the new diameter of the top of the cup can be calculated. If we use θ to describe the angle of the wall of the cup from vertical then, because the side of the cup l remains fixed, the top diameter can be calculated. (The default angle of my cup was not zero degrees, but 15 degrees, more of this later …)

Plotting the volume of the cup against the angle of the side reveals the following theoretical curve:

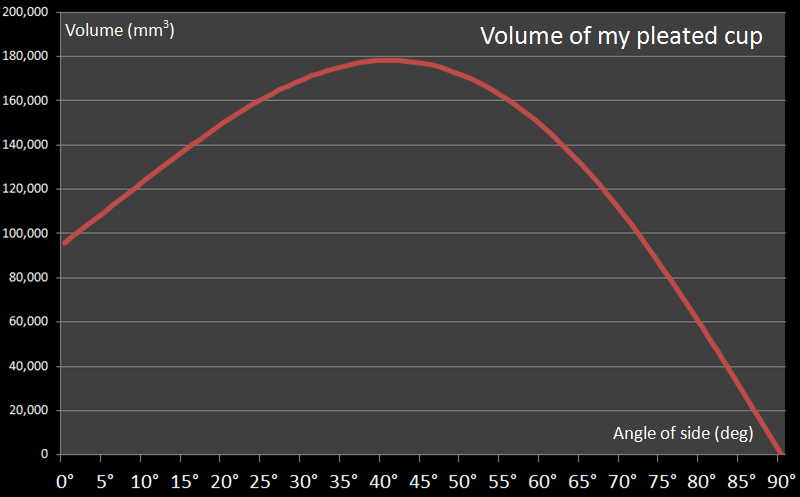
As you can see, as the angle of the sides increases, so does the volume of the container … up to a certain maximum point. Then, because the cup gets flatter and flatter, the carrying capacity decreases again until, at 90°, it turns into a flat plate and can hold no ketchup at all!

But we don't start straight

As previously mentioned, the supplied angle of my cup was 15° to the vertical.

This 15° setting is the base line for the payload capacity of the cup. If one did not adjust the pleats in anyway, the default volume of ketchup that could be held is measured at this angle. Normalizing to this value, we can adjust the axis to show a ratio relative to this value. Here is the chart with the new axis:

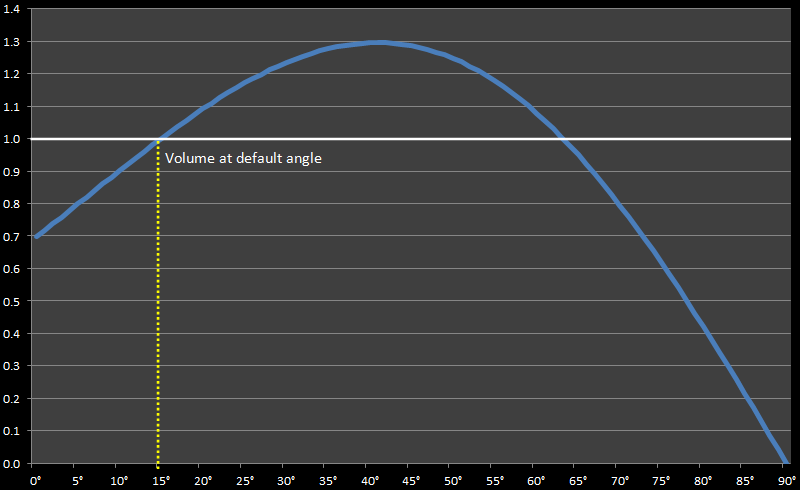
At 15° we see the ratio is 1.0. With the particular dimensions of the cup I am using, the peak carrying capacity is 1.296 x that obtained at the default angle, and this can be achieved by setting the walls to an angle of 41°

This is a 30% increase from base carrying capacity. Far shorter than the doubling implied by the comment on the meme!

(Interestingly, the 15° default angle makes a huge difference to the default carrying capacity of the cup. As you can see from the above curve, if the cups were supplied with straight vertical sides, their capacity would be 30% lower!)

Also worth mentioning is that the ratio stays over 1.0 until 64° (using the dimensions of my cup). Any angle between 15°–64° will increase the carrying capacity of your cup, but if you "Overcook"" your angle beyond this point, you will reduce the volume of your favorite condiment!

Nobody likes to get their fingers dirty!

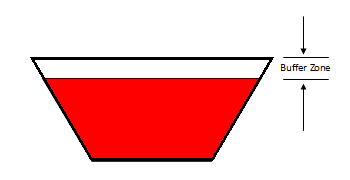
The above calculations were based on the assumption that one fills the paper cup container all the way to the brim!. I don’t know about you, but I certainly never do this. It’s bad move. If you try to pick-up a totally full cup, it distorts and ketchup oozes over the top, over your fingers, and makes a mess on the tray. It’s always safe to leave a buffer zone at the top of the cup.

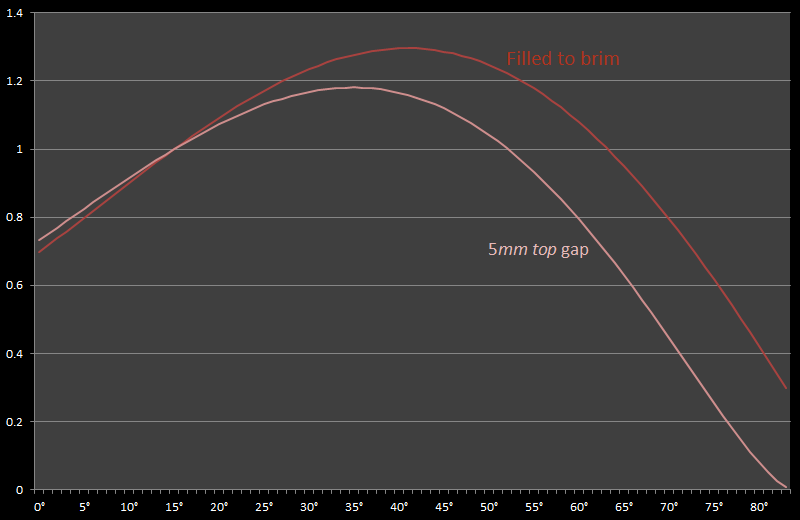
If we assume a 5 mm buffer zone (there is always a gap of this distance between the top of the rim and the top of the condiment), then this adjusts the curve, as seen below.

A 5 mm buffer moves the optimal angle back (in our case) to 35°, and reduces the benefit to less than 20%.

You'd better get that second cup after all!

Subliminal Message

Are you hungry now?

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.