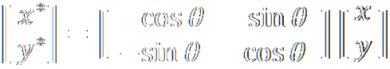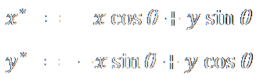Rotating Images
Recently I wrote about How to draw a straight line (using linear regression).
In this posting I’m going to talk about how to rotate an image …
 |
… but first a little Soap Box. These days, we’re spoiled with having super-fast processors and high-level libraries to do many things. Well, spoiled is not quite the correct verb, what I mean is that, unless you’re working on some core system code or an incredibly time sensitive component, you don’t have to code everything from scratch. Most of the time, this is a good thing; it means you can focus your brain cells on coding the problem, not on building the blocks. If you want to sort an array, you call a sort function. If you want a dialog box you call one up. If you want to rotate a bitmap, well, there’s a function for that. |
|
You don’t need to know how an internal combustion engine works to drive a car. This is progress. After all, if you want to build a house you go to the builders supply store and buy some bricks and some planks of wood. You don’t dig up clay and chop down trees. People better skilled than you at making bricks have made the bricks for you. People with better tools have made smooth straight wooden beams for you. You can focus on building a masterpiece. It’s the same when writing code. |
 |
 |
Indulge me, however, as I reminisce. Back when I started programming games in 6502 assembly language, you had to do everything yourself. You wanted to draw a line?, well you’d better write your own code to do it. You wanted to know if that line is visible on screen, or needs clipping? Code if yourself! You wanted to draw and move sprites around screen?, Yes, you guessed it … 
|
Better coding through understanding
I’m not suggesting a Luddite revolution. I’m not suggesting that everyone should burn their libraries; far from it. Today’s coding masterpieces are architected on the shoulders of other building blocks.
However, an understanding about how things work will make you a better programmer. Knowing how an underlying function will process your data will help you design your data structures to be sympathetic. Knowing how a library function works under the covers will, one day, help you solve an analogous higher level problem sometime in the future.
Plus, it’s just fun to learn about! You might not make your own bricks, but it’s fun to watch How it’s made (Series 2 – Episode15)
Bitmaps
A typical computer image these days uses 24 bits to represent the color of each pixel. Eight bits are used to store the intensity of the red part of a pixel (00000000 through 11111111), giving 256 distinct values. Eight bits are used to store the green component, and eight bits are used to store the blue component.
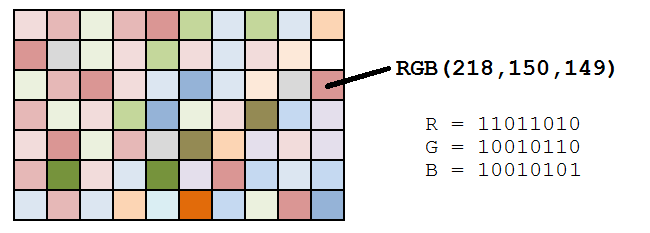 |
The diagram on the left shows how each pixel of an image can be described by three 8-bit binary numbers. |
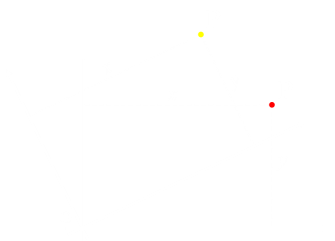
Each pixel has a coordinate pair (x,y) describing its position on two orthogonal axes from defined origin O. It is around this origin we’re going to rotate our image.
 |
What we need to do is take the RGB values at every (x,y) locatioon, rotate it as needed, and then write these values in the new location. |

|
To complete the rotation we need to write the RGB value for each pixel in the new location. The (x,y) coordinates relative to the axes are the same; what we have done is rotate the coordinate frame of reference by an angle θ. |
 |
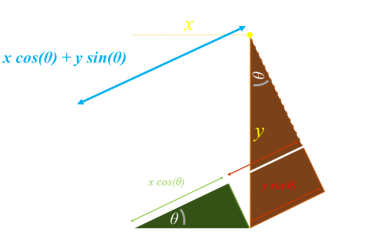 |
Using some High School geometry we can work out the relationship between the source coordinates (x,y) and the destination coordinates (x*,y*)
It is convenient to write in a matrix format as shown above. You might remember this from school. |
You spin me right round …
 |
Here is our source image. By translating the coordinate frame we can place the origin at the centroid, and it is around this we will rotate it.
The matrix expands out as above. We can loop over the image for each (x,y) coordinate and find its new destination. |
 |
Here is the result with a rotation of θ = 15° It's certainly worked. The image has been rotated, but what are all those dots? This is a problem called aliasing. It's the same reason that we see jagged staircases on lines drawn on low resolution screens at angles other than horizontal and vertical. Raster screens are digital, and pixel boundaries are at quantized locations. |
|
Multiplying by sines and cosines on the integer coordinates of the source image gives real number results, and these have to be rounded back to integers again to be plotted. Sometimes this number rounding means the same destination location is addressed more than once, and sometimes certain pixels are missed completely. When the pixels are missed, the background shows through. This is why there are holes. |
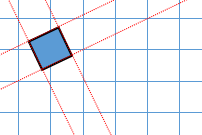 |
Aliasing
The aliasing problem gets worse when angles are closesr to the diagonals. Here are a few examples of images at different rotations:
0°  |
35°  |
45°  |
170°  |
What can we do about this? There are a variety of solutions. One of them is to oversample the source image. We can pretend that each of the original source pixels is really a grid of n x n smaller pixels (all of the same color), and calculate the destination coordinates of each of these subpixels and plot these.
A more refined way is called Area Mapping. For this, you invert the problem, and for each destination pixel, you find which four partial source pixels that it was created from. The color for the destination is calculated by the area-weighted average of the four source pixels (The source pixels that contribute more to the destination pixel have a greater influence on its color). This algorithm not only ensures that there are no gaps in the destination, but also appropriately averages the colors (ensuring both a smoother image and also keeping the average brightness of the rotated image constant).
However, there is a more elegant method, and this is the method that was used many years ago when computing power (and memory) were at a premium and every processor cycle worth its weight in gold. It is called the three shear rotation method. It's so clever that it's worth sharing in full detail.
Three shears
The heart of this method is the expansion of the single 2D rotation matrix into a three different matrices:
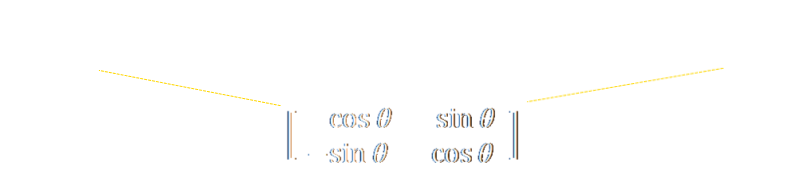
There are some very interesting properties of these three matrices:
The three matrices are all shear matrices.
The first and the last matrices are the same.
The determinant of each matrix is 1.0 (each stage is conformal and keeps the area the same).
As the shear happens in just one plane at time, and each stage is conformal in area, no aliasing gaps appear in any stage.
In times-past, when floating point and trig calculations were expensive, these properties were very important. Because only one plane was being modified at once, no additional memory was needed as the code could simple walk down the raster line making the changes it needed. Pretty cool.
Let's see this is action:

In the first shear operation, raster columns are simply shifted up and down relative to each other. The shearing is symmetric around the center of the image. It's analogous to shearing a deck of playing cards.
The second shear operation does a similar thing on the previous image, but this time does the shearing left to right.
The final shear is the same as the first operation; this time applied to the intermediate image.
No gaps! How elegant is that? We just rotated an image an arbitrary amount (smoothly) using three shear operations!
More examples
This is so cool it's worth seeing a few other examples.
Below are rotations of a test card of random shapes (so you can see the effect of the shears), a Spitfire, and Tigger. For each image, I've shown the source, the results of applying the three shear matrices in order and, for comparison, the image produced by the standard 2D rotation matrix (sometimes called a rotation by selection).
Source Image
 |
 |
 |
Shear #1
 |
 |
 |
Shear #2
 |
 |
 |
Shear #3 [Result]
 |
 |
 |
Standard 2D rotation matrix (rotation by selection)
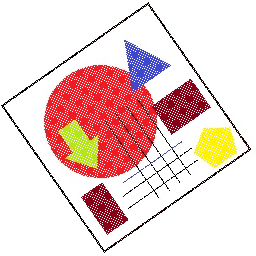 |
 |
 |
Want to see some magic?
Do you still use Microsoft Paint, or some other under-powered paint package that does not allow you to rotate an image by an arbitrary angle? Ever been frustrated by this?
 |
The (built in) rotation option only allows you to rotate the image in multiples of 90° Those are the easy options to code. What if you wanted to rotate your image by, say, 27°? |
|
Well, thankfully, Microsoft equipped paintbrush with a couple of useful functions, these are resize and shear (which they call skew) We can apply the three stage shear principle/concept we have just learned. The two basic tools provided to us in the paint package enable us to produce an arbitray rotation! (The math is modfied slightly because paint applies the actions to the selected region, not a centroid, but it's the same thing we are doing.) |
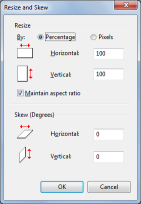 |
Coin spinning
I'm going to show you how you can rotate the image of the half-dollar coin below by 27°
 |
I'm using a coin, on purpose, because it is circular and you can see the effects of the shears. We can also see, at the end, if there is any distortion. I obtained my image from Wikimedia Commons, just incase you want to play along at home and repeat these steps. |
Step #1 Horizontal Shear
Select the image you want to rotate. The image is going to be rotated around the center of the selection. Make sure you leave sufficient space around the image for expansion as we distort the image.
With the region selected, click on the Resize button on the Painbrush toolbar and enter in the desired skew (in degrees) in the horizontal plane.
In the case, I've entered 27°
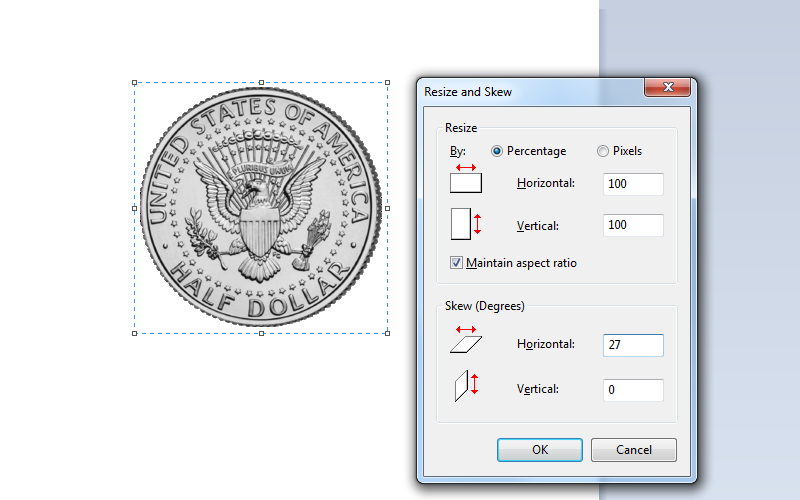
Step #2 Vertical Scale
Now we need to scale in the vertical plane. Without adjusting the selected region, click on the Resize button again.
NOTE - We only want to scale in the vertical plane, so make sure to uncheck the box 'Maintain aspect ratio'
The exact value to enter into this box is based on a calculaton. You'll need to use the forumla below to get a scaling factor, and round it to the nearest number.
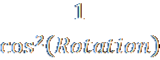
In my case, for 27° the answer is 1.2596, so I've rounded this to 126% percentage scaling.
(Make sure your calculator is set into Degrees and in Scientific mode. Type in your rotation, hit the cos button, then x2 then 1/x button).
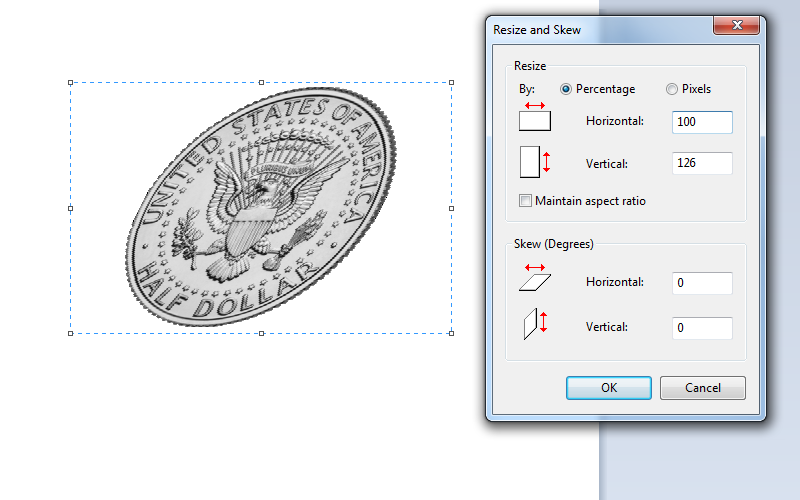
Step #3 Vertical Shear
This one is easy. Click the Resize button once more and skew the image a negative number of degrees in the vertical plane.
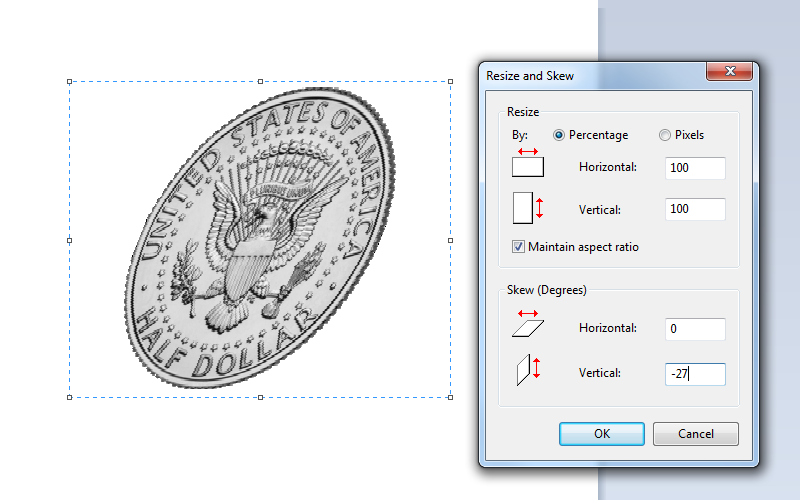
Step #4 Global Resize
One last step. We need to shrink the image back to the correct size.
To calculate the scaling factor we need to take the cos of the rotation angle.
For 27°, cos(27) = 0.8910 so we use this as the scale factor (rounded to 89%).
NOTE - This time make sure the 'Maintain aspect ratio' box is checked, as we need to apply this to both axis.
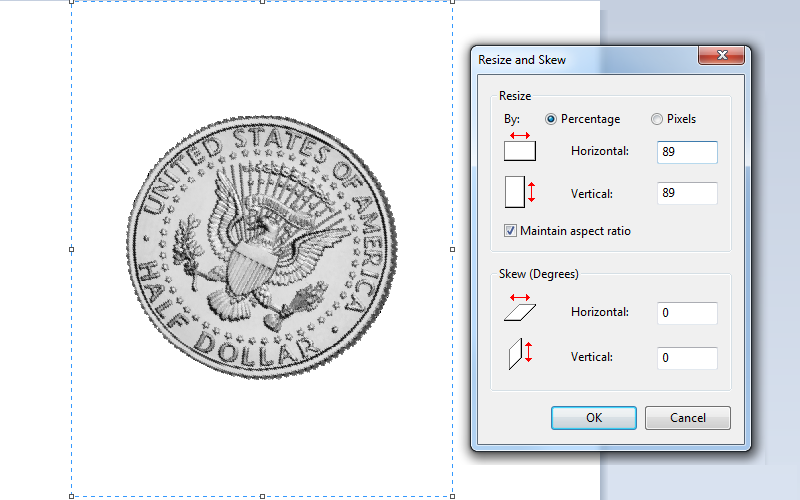
And we're done …
Let's see our results:

How did we do?
The image on the left is the source image. The image on the right is our rotated image. Pretty good.

OK, I'm a geek, but I think this is the coolest thing you'll see today!
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.