Why do pipes burst they way they do?
We’re currently experiencing colder-than-seasonal weather here in Seattle. This is causing a lot of problems with burst water pipes. Here is a picture of a couple of issues suffered by a friend of mine Ian.
| Photo Credit: Ian Mercer |

Why do water pipes burst, and why do they always fail the same way? These are two interesting questions.
 |
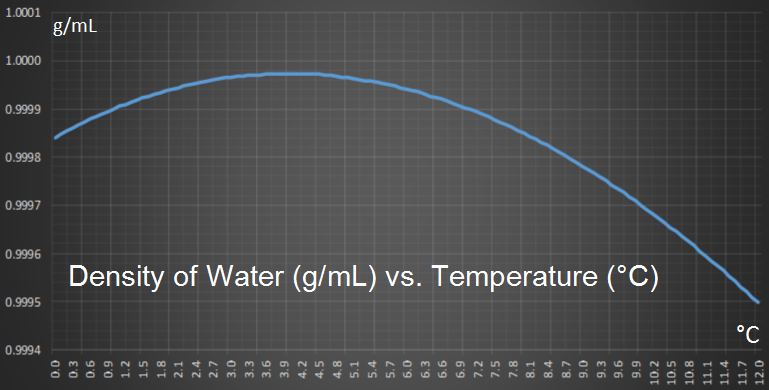
Water pipes burst because the water inside them expands is it gets close to freezing, and this causes an increase in pressure inside the pipe. When the pressure gets too high for the pipe to contain, it ruptures. We grew up with water all around us and so this expansion phenomenon seems natural, but interestingly, it is a chemical anomaly. Most liquids do not expand just before transition to solid. You should be thankful for this; it is one of the reasons that life exists. When a liquid cools the molecules slow down (temperature really is just a measure of the average kinetic energy of the molecules). This slowing down allows the molecules to get closer together and increases the density of the liquid. This happens with water too, and when water is cooled down, it gets denser and denser, down to 3.98°C then, something interesting occurs; it starts to expand again. |
You can see this effect on the graph below which shows how the density of pure water changes with temperature (at one atmosphere). You can see how density reaches a maximum at 3.98°C.
Because of the shape of a water molecule, it is slightly polarized. The electrons buzzing around it are more likely to be on one side of the molecule than the other (called a dipole), and this asymmetry creates a slight potential. Water molecules are attracted to each others’ opposite sides. These potentials create weak bonds that are called Hydrogen Bonds. Hydrogen bonds, whilst not as strong as covalent bonds or ionic bonds, are stronger that van der Vaals forces.
 |
This extra hydrogen-bond ‘glue’ holding water molecules together is the reason why water is a liquid at everyday temperatures and pressures (another one of the reasons life exists). Other chemical compounds similar to H2O, but without the benefit of Hydrogen bonds, are all gases in typical Earth temperature ranges. |
|
The Hydrogen-bonds in water are also the reason why water has such a high specific heat capacity (the amount of energy required to raise the temperature of water one degree); this helps dampen our weather and stops the Earth changing in temperature too rapidly. It also means that water is great for carrying energy around (like in power stations and hydronic central heating systems). It’s also why it takes a lot of energy to boil a kettle to make a nice cup of tea! |
 |
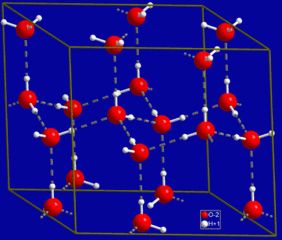 |
As water cools, like other liquids, the molecules slow down and get denser. A competing force, however, is the desire for the water molecules to align with other water molecules based on their Hydrogen bonds, and this causes expansion. Below the temperature of 3.98°C down to 0°C, this alignment expansion process wins out against the desire of slower molecules to get closer, and density decreases. Whilst not completely understood, it is this expansion that causes beautiful snowflakes to form with their characteristic six points.
|
This decrease in density continues until the water finally freezes to form ice. Water expands to form ice which has a volume up to 9% greater than the water it came from. It is this reason that icebergs float (being less dense than the water they displace).
|
Again, it seems natural to us that ice floats, because we grew up this all effect all around us, but this is atypical. Most other liquids, when freezing, do not form a solid ‘crust’ on top. As they cool, the solid formed, being denser, drops to the bottom of the cooling liquid and the solid grows up from the bottom! |
 |
 |
This irregular behavior of water is yet another reason that life exists. When water freezes, it floats to the top, forming a skin which insulates the water below. When a river or lake freezes on top, life continues below in the liquid left underneath. |
Why do pipes split longitudinally?
We know now that is it the expansion of water causing excess pressure inside the pipe that causes it to rupture. The second question to answer is why they always seem to burst parallel to the direction of the pipe?
(Regular readers of my blog will find a lot of duplication in this topic to my posting about why sausages split the way they do. It's the same reason).
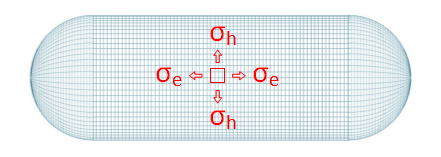 |
Let’s model a section of water pipe as a thin-walled cylinder with hemispherical end caps. What does that mean? It means that we're only concerned with modelling the wall of pipe (the thing that fails). Thin-walled means that the thickness of pipe is considered negligible compared to the diameter of the pipe (in this way, we only need to consider the tension in the wall). |
According to Pascal's Principle we'll assume the pressure of the fluid inside the pipe is uniform.
Longitudinal Stress and Hoop Stress
Because of cylindrical symmetry we don't need to worry about shear stress in the pipe wall. If we examine a small square on the surface we can consider the forces resolved in two perpendicular directions: Hoop Stress which runs around the pipe like a ring, and Longitudinal Stress which runs axially up the pipe.
Stress is defined as Force per Area, and can be calculated by dividing the forces experienced over the cross-section upon which they are applied. We'll use the Greek letter σ to represent stress.
| σh | Hoop Stress |
| σe | Longitudinal Stress |
| r | Radius of pipe |
| t | Thickness of wall |
| P | Pressure inside pipe |
Longitudinal Stress
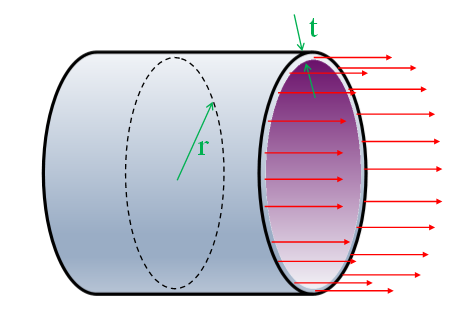 |
Imagine a cross section cut through the pipe revealing a circular section. Axial stress passes passing longitudinally through this ring section and must balance out the pressure force experienced internally (equilibrium). σe = Force / Area |
The force pulling the pipe apart, end-to-end, is the internal pressure multiplied by the cross sectional area.
Force = Pressure x (Cross-sectional area of pipe)
Force = Pπr2
The area this force is applied over is the thin ring of wall around the edge:
Area = 2πrt
Combining these, we can calculate the longitudinal stress:
σe = Pπr2 / 2πrt
σe = Pr / 2t
(You can see from the derivation of this stress calculation that the longitudinal stress is proportional to the cross section area of the pipe.)
Hoop Stress
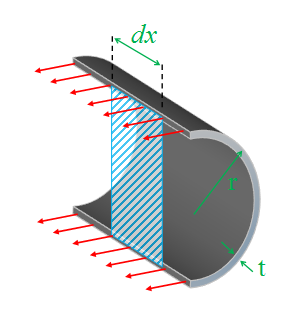
To calculate the hoop stress, we look at a slice down the center line of the pipe and consider the forces in a small hoop of width dx.
|
As before we calculate the force by the internal pressure multiplied by the area it is applied over: Force = P.2r.dx The area this force is applied over is the two parts of the ring at the top and bottom of the cylinder: Area = 2.t.dx Combining these, we can calculate the longitudinal stress: σh = P.2r.dx / 2.t.dx σh = Pr / t |
 |
Result
Photo Credit: Ben Freeman |
Comparing the two results, we can see that the hoop stress in the wall is twice that of the of the longitudinal stress. It should, therefore, be no surprise that pipes burst through a hoop failure and create a rupture that runs perpendicular to the line of maximum stress.
Insulate your pipes this Winter! |
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.


