Dealer Button Bias
|
When playing card games with forced bets, such as Texas Hold’em Poker, the location of the dealer progresses around the players one position for every hand. This advancement of the dealer helps balance the game because everyone gets a turn in order. This is as important as the player immediately to the left of the dealer typically has to make an automatic bet called the small blind, and the next person around places a bet called the big blind. Players who have made blind forced bets are already committed to the pot in various degrees (irrespective of the cards they hold), and this helps mix-up the game. In addition, requiring bets each round keeps the game moving with players participating in hands with cards they might otherwise not have played (if you fold every hand you’ll still gradually lose money as the blinds pass you). |
 |
 |
The position of the dealer (even if this is person is not the person who physically deals the cards, such as games with professional dealing staff), is typically marked with a dealer button, which is a puck that moves around the table. |
Where to start
 |
This does leave the question, however; Where should the dealer button initially begin? Who gets the dealer button first? |
|
One common strategy is called the First Ace. The deck is shuffled, and cards dealt out one-at-a-time face up, going around the players seated at the table. This continues around and around until the first ace is exposed. The person who is deal the first ace becomes the dealer for the first hand. |
 |
 |
At first blush, this seems pretty fair, after all, the deck is randomly shuffled. However this system has bias (for more on bias and shuffling you might be interested in this article), with different odds of getting the dealer button depending on position. |
Bias
The system has bias for two reasons:
It’s instant death. As soon as an ace is turned up, the competition stops. Those players further downstream might not even had chance to receive a card.
There is more than one ace. If there were only one ace, this system would be fair, but with more than one ace, the concentration of aces changes non-linearly as more cards that are not aces are drawn.
Thoughts
|
If you desired to the dealer, where is the best place to sit? Is getting a card before the others downstream of your more advantageous (since the game instantly stops if you get an ace), or is it better to be a little later in the table as the concentration of aces in the unseen deck increases with each card exposed that is not-ace? The chances of drawing an ace improve the longer the game runs, but you have to survive long enough to get to the state that allows you to exploit this advantage. Do these things cancel? … The odds are not quite that simple either because, if an ace is not seen after everyone has had one card, we continue dealing around, so the true expected probabilities need to account for the possibility of getting the first ace over all passes. |
  |
Math
Let's look at the probabilities. The math is actually pretty easy.
There are four aces in a deck of fifty-two cards.
The first person to receive a card (first card dealt = Pr1) has a 4 in 52 chance of getting an ace. (Pr1 ≈ 7.69%)
The probability that the second card drawn is an ace Pr2, can be calculated because the first card drawn must not be an ace (48 chances in 52) AND then one of the aces is then drawn (4 chances in 51). To AND probabilities we multiply them. (Pr2 ≈ 7.24%)

The denominator gets smaller with each card drawn. The probability of getting the first ace on card n, is the product of not drawing an ace on the first draw, or the second, or the third … or the n-1th card, then drawing one of the aces out of the cards left.
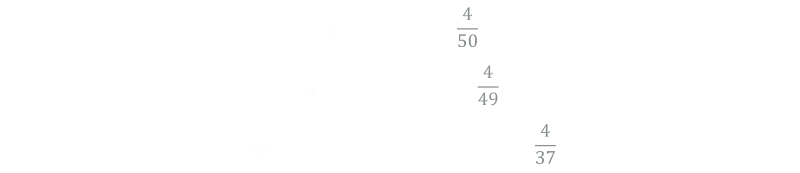
Here is graph of the probabilities. On the x-axis is the number of cards left in the deck before the card is drawn. The y-axis shows the probability of getting the first ace on that card:

These are the probabilities for each individual card. We're almost there. Now all we need to do is add up the probabilities for the the cards we might possibly get. If there are two players, then the first player will get cards #1, #3, #5 … and second player will get cards #2, #4, #6 …
For the first person to get the ace, it's probability the ace is card #1 OR card #3 OR card #5 OR … To OR probabilities we add them.
If there are three players, then the first player will receive cards #1, #4, #7 …
How Many People at the table?
Below is a table showing which players get which card. On the far left is the number of cards left in the deck. Each row is one less card drawn. Next is the probability that the first ace will be drawn on the turn of the next card. (All these percentages add up to 100%; the ace has to occur in one of these positions). We never need to get below four cards. If there are four cards left, we are certain the next drawn card will be an ace (it's just, however, amazingly unlikely that we'll get to this state as we'll have to have revealed all forty-eighty others cards and shown them not to be aces!)
To the right are which players get which card if the cards are dealt out cyclically. I've given figures for up to 13 people at the table.
| Deck | Players | # | Percent | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 52 | 7.6923% | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 51 | 7.2398% | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 50 | 6.8054% | 1 | 1 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 49 | 6.3888% | 1 | 2 | 1 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 48 | 5.9895% | 1 | 1 | 2 | 1 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 47 | 5.6072% | 1 | 2 | 3 | 2 | 1 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
| 46 | 5.2415% | 1 | 1 | 1 | 3 | 2 | 1 | 7 | 7 | 7 | 7 | 7 | 7 | 7 |
| 45 | 4.8920% | 1 | 2 | 2 | 4 | 3 | 2 | 1 | 8 | 8 | 8 | 8 | 8 | 8 |
| 44 | 4.5585% | 1 | 1 | 3 | 1 | 4 | 3 | 2 | 1 | 9 | 9 | 9 | 9 | 9 |
| 43 | 4.2405% | 1 | 2 | 1 | 2 | 5 | 4 | 3 | 2 | 1 | 10 | 10 | 10 | 10 |
| 42 | 3.9376% | 1 | 1 | 2 | 3 | 1 | 5 | 4 | 3 | 2 | 1 | 11 | 11 | 11 |
| 41 | 3.6495% | 1 | 2 | 3 | 4 | 2 | 6 | 5 | 4 | 3 | 2 | 1 | 12 | 12 |
| 40 | 3.3758% | 1 | 1 | 1 | 1 | 3 | 1 | 6 | 5 | 4 | 3 | 2 | 1 | 13 |
| 39 | 3.1161% | 1 | 2 | 2 | 2 | 4 | 2 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| 38 | 2.8701% | 1 | 1 | 3 | 3 | 5 | 3 | 1 | 7 | 6 | 5 | 4 | 3 | 2 |
| 37 | 2.6374% | 1 | 2 | 1 | 4 | 1 | 4 | 2 | 8 | 7 | 6 | 5 | 4 | 3 |
| 36 | 2.4176% | 1 | 1 | 2 | 1 | 2 | 5 | 3 | 1 | 8 | 7 | 6 | 5 | 4 |
| 35 | 2.2104% | 1 | 2 | 3 | 2 | 3 | 6 | 4 | 2 | 9 | 8 | 7 | 6 | 5 |
| 34 | 2.0153% | 1 | 1 | 1 | 3 | 4 | 1 | 5 | 3 | 1 | 9 | 8 | 7 | 6 |
| 33 | 1.8321% | 1 | 2 | 2 | 4 | 5 | 2 | 6 | 4 | 2 | 10 | 9 | 8 | 7 |
| 32 | 1.6604% | 1 | 1 | 3 | 1 | 1 | 3 | 7 | 5 | 3 | 1 | 10 | 9 | 8 |
| 31 | 1.4997% | 1 | 2 | 1 | 2 | 2 | 4 | 1 | 6 | 4 | 2 | 11 | 10 | 9 |
| 30 | 1.3497% | 1 | 1 | 2 | 3 | 3 | 5 | 2 | 7 | 5 | 3 | 1 | 11 | 10 |
| 29 | 1.2101% | 1 | 2 | 3 | 4 | 4 | 6 | 3 | 8 | 6 | 4 | 2 | 12 | 11 |
| 28 | 1.0804% | 1 | 1 | 1 | 1 | 5 | 1 | 4 | 1 | 7 | 5 | 3 | 1 | 12 |
| 27 | 0.9604% | 1 | 2 | 2 | 2 | 1 | 2 | 5 | 2 | 8 | 6 | 4 | 2 | 13 |
| 26 | 0.8496% | 1 | 1 | 3 | 3 | 2 | 3 | 6 | 3 | 9 | 7 | 5 | 3 | 1 |
| 25 | 0.7476% | 1 | 2 | 1 | 4 | 3 | 4 | 7 | 4 | 1 | 8 | 6 | 4 | 2 |
| 24 | 0.6542% | 1 | 1 | 2 | 1 | 4 | 5 | 1 | 5 | 2 | 9 | 7 | 5 | 3 |
| 23 | 0.5688% | 1 | 2 | 3 | 2 | 5 | 6 | 2 | 6 | 3 | 10 | 8 | 6 | 4 |
| 22 | 0.4913% | 1 | 1 | 1 | 3 | 1 | 1 | 3 | 7 | 4 | 1 | 9 | 7 | 5 |
| 21 | 0.4211% | 1 | 2 | 2 | 4 | 2 | 2 | 4 | 8 | 5 | 2 | 10 | 8 | 6 |
| 20 | 0.3579% | 1 | 1 | 3 | 1 | 3 | 3 | 5 | 1 | 6 | 3 | 11 | 9 | 7 |
| 19 | 0.3014% | 1 | 2 | 1 | 2 | 4 | 4 | 6 | 2 | 7 | 4 | 1 | 10 | 8 |
| 18 | 0.2512% | 1 | 1 | 2 | 3 | 5 | 5 | 7 | 3 | 8 | 5 | 2 | 11 | 9 |
| 17 | 0.2069% | 1 | 2 | 3 | 4 | 1 | 6 | 1 | 4 | 9 | 6 | 3 | 12 | 10 |
| 16 | 0.1681% | 1 | 1 | 1 | 1 | 2 | 1 | 2 | 5 | 1 | 7 | 4 | 1 | 11 |
| 15 | 0.1345% | 1 | 2 | 2 | 2 | 3 | 2 | 3 | 6 | 2 | 8 | 5 | 2 | 12 |
| 14 | 0.1056% | 1 | 1 | 3 | 3 | 4 | 3 | 4 | 7 | 3 | 9 | 6 | 3 | 13 |
| 13 | 0.0813% | 1 | 2 | 1 | 4 | 5 | 4 | 5 | 8 | 4 | 10 | 7 | 4 | 1 |
| 12 | 0.0609% | 1 | 1 | 2 | 1 | 1 | 5 | 6 | 1 | 5 | 1 | 8 | 5 | 2 |
| 11 | 0.0443% | 1 | 2 | 3 | 2 | 2 | 6 | 7 | 2 | 6 | 2 | 9 | 6 | 3 |
| 10 | 0.0310% | 1 | 1 | 1 | 3 | 3 | 1 | 1 | 3 | 7 | 3 | 10 | 7 | 4 |
| 9 | 0.0207% | 1 | 2 | 2 | 4 | 4 | 2 | 2 | 4 | 8 | 4 | 11 | 8 | 5 |
| 8 | 0.0129% | 1 | 1 | 3 | 1 | 5 | 3 | 3 | 5 | 9 | 5 | 1 | 9 | 6 |
| 7 | 0.0074% | 1 | 2 | 1 | 2 | 1 | 4 | 4 | 6 | 1 | 6 | 2 | 10 | 7 |
| 6 | 0.0037% | 1 | 1 | 2 | 3 | 2 | 5 | 5 | 7 | 2 | 7 | 3 | 11 | 8 |
| 5 | 0.0015% | 1 | 2 | 3 | 4 | 3 | 6 | 6 | 8 | 3 | 8 | 4 | 12 | 9 |
| 4 | 0.0004% | 1 | 1 | 1 | 1 | 4 | 1 | 7 | 1 | 4 | 9 | 5 | 1 | 10 |
If there are four players at the table, the person sitting in position #1 will get cards with probabilities :
7.6923% + 5.9895% + 4.5585% + 3.3758% + … + 0.0129% + 0.0004% = 28.0288%
(Obtained by reading down the column marked 4 and summing all percentages for grids that contain a one in the matrix).
You can immediately see that this is higher than that 25% we'd expect if this was random. Dealing to the first ace has bias.
All results
It's trivial if there is only one player; he's bound to get the first ace with 100% certainty! Here are the results for table sizes 2-13. For each one I've shown the player position, the percentage chance for someone seated in that location (obtained by summing the percentages), and the absolute +/- percentage difference from the expected result that pure random should give.
|
Players = 2
|
Players = 3
|
Players = 4
|
Players = 5
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Players = 6
|
Players = 7
|
Players = 8
|
Players = 9
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Players = 10
|
Players = 11
|
Players = 12
|
Players = 13
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Interestingly, whilst absolute percentages are shown, in terms of relative percentage, it is over twice as likely you will get the dealer button, for instance, if you are sitting in position #1 of a twelve player table than if you were sitting in position #12.
What to do?
Now that we know the first ace strategy is biased, what should we do if we really wanted the selection to be fair?
 |
Two obvious solutions come to mind. The first is to deal, not until the first ace, but until one particular ace (such as the Ace of Spades) is revealed. The person who receives this card is the dealer. (But here, if the number of players is not an exact multiple for 52, then some people would get more cards than others. So, if the defined Ace has not appeared after everyone has received the same number of cards, the cards should be collected again, re-shuffled and the experience repeated!) The second is to deal everyone just one card each, and the highest card wins. If there is a tie for first place, then all those tied can be dealt a second card, and a third … as necessary until a high distinct card is obtained. Shuffle up and deal! |
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.

