100 Prisoners Escape Puzzle
|
Recently, I wrote about a classic prisoner escape puzzle which, at first glance, appeared impossible. There’s another classic, impossible sounding, prisoner escape puzzle called the 100 prisoner problem. It was first written about by Danish computer scientist Peter Bro Miltersen. In this puzzle there are 100 prisoners, each given a distinct number 1-100. The jailer has decided to give all the prisoners a chance to escape. He prepares a challenge, and if every single one of the prisoners passes, they are all free to go. If even one of them fails, they all die. 
|
 |
The Challenge
The jailer goes into a secret room and prepares 100 boxes with lids. He labels these boxes 1-100. Then he prepares 100 tickets, one for each prisoner, and labels these tickets 1-100. Finally, he shuffles the tickets thoroughly, and puts one ticket in each box, closing the lid behind it. The prisoners cannot see any of these preparations.

The challenge is now on. He fetches each prisoner, one-by-one, into the box room and tells the prisoner that they must find the box that contains their ticket. They attempt to do this by opening boxes. They are allowed to open up to half the boxes in their search. If they succeed in finding their own number, they win. If they have not found their ticket after examining 50 boxes, they fail.
 |
In order for the prisoners to escape, all prisoners have to win. What are their chances of escape? After opening a box and examining its contents, the lid is closed again. The position of tickets cannot be changed. No messages can be left behind for prisoners yet to come to decode. The prisoners are allowed to confer before the challenge begins. What is their optimal strategy? Bonus Question: If comrade (not party to the challenge) is able to sneak into the room beforehand, examine the locations of all the tickets and (optionally) swap just two of the tickets over (but not able to communicate what change he made), what strategy should he adopt to improve the prisoners' chance of escape? |
Pretty Unlikely
At first glance, this seems a pretty hopeless problem. In fact, it appears that the chances of all the prisoners finding their own tickets is microscopically small. After all, there is no way for the prisoners to communicate any information to each other.
With just one prisoner, he has a 50:50 chance. There are 100 boxes, and he gets to open (up to) 50 boxes looking for his ticket. If he opens the boxes at random he’ll open half the boxes, and his ticket will, or, will not be in the half he opens. His chance of success is ½.
With two prisoners, if both select at random, it would also by ½ chance of success each, so for two prisoners, it is ½ × ½ = ¼.(They will succeed one time in four).

For three prisoners it’s ½ × ½ × ½ = ⅛.
With 100 prisoners, it’s ½ × ½ × … ½ × ½ (100 times).

This is:
Pr ≈ 0.000000000000000000000000000008
That’s a pretty small chance. It appears as though the prisoners are as good as dead.
Unbelievable answer
 |
If each prisoner guesses totally at random, it's incredibly unlikely they will escape. There is a strategy that the prisoners can follow that gives them a greater than 30% chance of escaping. This is a staggeringly unbelievable result (if you’ve not heard the puzzle before). Greater than 30% for all 100 people is so good that it's already better than two prisoners guessing totally at random! How is this possible? |
Clearly, no individual prisoner can do better than 50% (there is no way for information to be communicated), however, just like the chess board puzzle (where there is information stored in the distribution of the coins), there is information stored in the arrangement of the tickets in the boxes. The tickets are not shuffled between subsequent prisoner visits, and we can use this information.
Solution
First I'll explain the solution, then I'll explain why it works.
The strategy is amazingly simple. First of all you open up the box corresponding to your own number. If you find your ticket, great!, if not you look up the number on the ticket in your box and that is the box your check next. You carry on this strategy … daisy-chaining your way through the boxes. That's it!
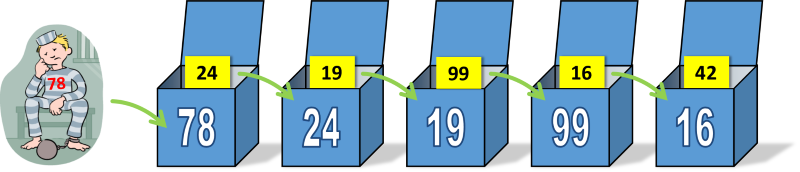
Eventually, you'll either find your number, or run past the 50 box limit. At first blush, it looks like this should not make any difference compared to simply picking boxes at random (and for any one individual, you'd be correct), but because all 100 prisoners will be using the same set of boxes, it makes a huge difference.
The beauty in this puzzle is not knowing the solution, but knowing why the solution works!
Why does this work?
|
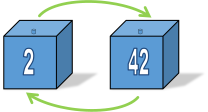
Every box contains one ticket, and the tickets are unique. This means that either a ticket is in the correct box, or it points to another box. As the tickets are distinct, there is only one ticket pointing to each box (and only one way to get to any box). |
 |
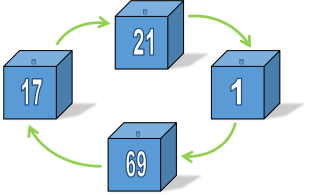 |
If you think about it, the boxes will form circular chains. A box can only be part of one chain because there is only one pointer in, and one pointer out of any box (programmers might see an analogy here with linked-lists). If a box is not a singleton (hosting its own ticket), it will be in a chain. Some chains might be as short as two boxes, some longer … |
|
Because the prisoner starts on the box of their own number they are, by definition, on the chain that contains their ticket (there is only one ticket that points to that box). By following the chain around they are guaranteed to end up at their ticket by following the chain. The only question is if they can do it before fifty boxes are opened! |
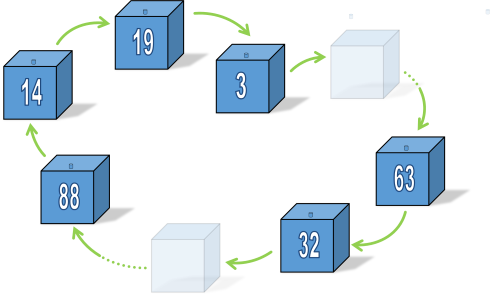 |
Chain Length
For everyone to succeed, the maximum chain length needs to less than fifty boxes long. If a chain is greater than fifty boxes, then those who have their ticket in that chain will fail (and thus everyone dies).
If the maximum chain length is less than fifty boxes long, then everyone succeeds!
Think about it for a second, there can only be one chain that is longer than fifty boxes in any configuration (there are only a hundred boxes in total, so if one chain is longer than 50, then the other(s) must be less than 50 in total).
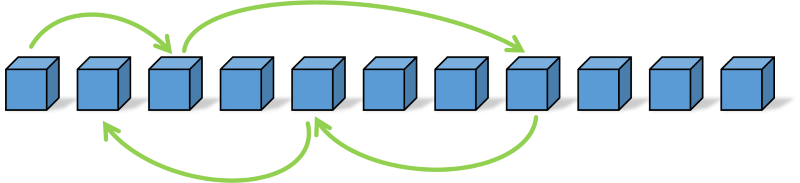
Chance of a long chain
After you've convinced yourself that, for success, the maximum chain length should be less than or equal to 50, and there can only be one chain in any set that has a chain greater than fifty, we can calculate the probability of success as:
Prwin = 1.0 - Prchance of a chain longer than 50
Little bit of math
 |
So, what we need to work out is the probability that long chains exist. For a chain of length l the number of ways the boxes can be arranged is (100 Choose l): 
In these collections of numbers, there are (l-1)! ways to arrange the tickets. The remaining tickets can be arranged (100 - l)! ways (and we don't care how, since we know none of these can be in a loop greater than 50). Combining these, the number of permutations that contain a chain of exactly length l is (>50): 
There are 100! ways of arranging the tickets, so the probability there is a chain of length l is just 1/l. This is a fascinating results because it is independent of the number of boxes! |
As we know there can be only one way to for a chain of any length > 50, the probability of success is:

Result
31.18% of the time, the length of the maximum chains formed will be less than 50 boxes and so every prisoner will be able to find his ticket before hitting the 50 box limit.
The probability of all the prisoners getting their ticket is 31.18%
Below is a graph showing the probabilities (on the y-axis) for all the chains of length l (on the x-axis). Red depicts all the failures (the curve here is simply the graph 1/l). Green shows the success (the calculation is a little more complex for this part of the graph as there are multiple ways the maximum length < 50 can be determined). The total probabilitty of the bars in green add up to the 31.18% chance of escape.
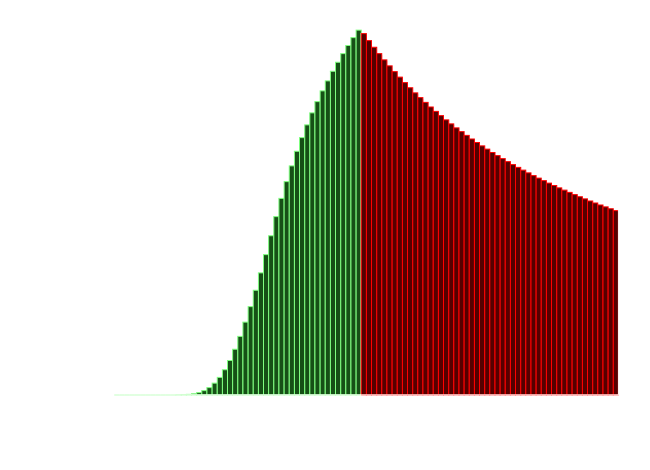 Image: Quartl (Wikipedia)
Image: Quartl (Wikipedia)
Harmonic Numbers (Optional Geek Part)
Those who read my blog regularly might recongize the appearance of our old friend Harmonic Numbers (most recently encountered in the posting how hungoever can you get?). Harmonic numbers are the sums of sequences of reciprocals.
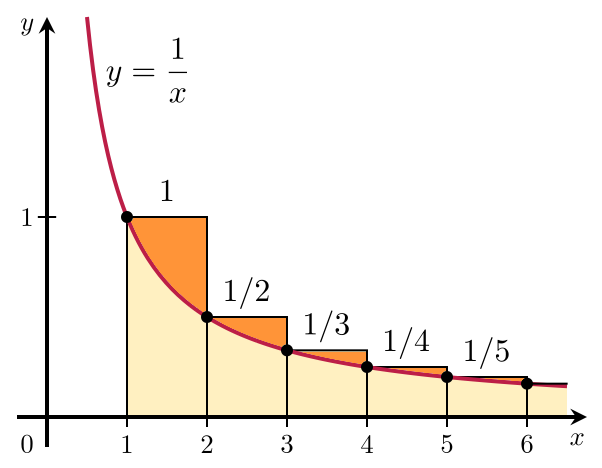
We can calculate the probability of losing the prison escape by subtracting the appropriate Harmonic Numbers.
Taken to the limit if, instead of 100 boxes, we have an arbitrary large number of boxes (let’s say that we have 2n boxes in total).
 |
 |
The Euler-Mascheroni constant γ cancels.
As the number of prisoners increases, if the jailer still allows them to open up-to half the boxes, the percentage chance of survivability asymptotes to 30.685%
(If you adopted the purely random guessing solution, as n increases, the probability of escaping drops to essentially nothing!)
Bonus Question
 |
Remember back to the beginning and the bonus question? What could our helpful comrade do to increase the chances of survival? Now that we know the solution, his strategy is clear. He should examine the tickets and look for the size of the longest chain. If the longest chain is less than 50 boxes long, he does not need to do anything (or I guess he could make a switch that does not increase that length, but that is optional). However, if there is a chain that is greater than 50 units, all he needs to do is switch two boxes that are in the chain to break the chain into two smaller pieces (he can switch two equally distant apart to make two smaller chains of half length each). The result of this is that there will never be a long chain, and it is guaranteed that all prisoners will be able to find their ticket. This is a pretty staggering result. Just swapping two numbers can assure escape! |
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.

