
	Advertisement

Newton and Pepys

Today we’re going to look at a classic probability problem. It’s not a new problem, in fact it’s many hundreds of years old. It can be traced back to two prestigious individuals in history: Sir Isaac Newton and Mr Samuel Pepys.

Sir Isaac Newton

Mr Samuel Pepys

Sir Isaac Newton, 1642-1727

English physicist and mathematician. Co-inventor of calculus, formulator of the Laws of Motion and Universal Gravitation. Builder of telescopes, theorist on optics, and confirmer of the heliocentric model of the cosmos and laws of planetary motion. President of the Royal Society, Cambridge Professor, and Master of the Royal Mint.

Mr Samuel Pepys, 1633-1703

English naval administrator and Member of Parliament. Chief Secretary to the Admirality to two Kings of England. Famous for keeping a private diary from 1660 to 1669 giving eyewitness accounts of life in London. President of the Royal Society.

The Problem

The origin of this problem is that Samuel Pepys, apparently a gambling man, asked Isaac Newton which of these three events had the highest probability of occurring:

Game A		Throwing 6 dice and getting at least one six.
Game B		Throwing 12 dice and getting at least two sixes.
Game C		Throwing 18 dice and getting at least three sixes.

Pepys, who had quite a considerable wager on this, thought that Game C was the more likely event, and wrote to Newton asking advice. A series of letters went backwards and forwards as the problem was discussed. Newton arrived at the correct solution, though historians and mathematicians debate that his correspondence about the matter contained a logical error in the explanation.

Have a think about the problem, yourself, for a few seconds before looking at the solution.

Which game do you think is more likely to win?

The Solution

The correct solution is that Game A is more likely to win than Game B which, in-turn, is more likely to win than Game C (if we use a 'fair' and unbiased set of dice). This is opposite to Pepy's gut feeling.

Proof

Let’s define the probability of rolling as six as p. For a fair dice this will be ¹/₆.

Game A

The easiest way to calculate this probability of this game winning is to work out the chance of it not happening, and subtract this from one (all probabilities must add up to 1.0).

Rolling a single dice, the chance of not rolling a six is: (1 - p)

In game A, we roll the dice six times, thus the probability of winning this game is:

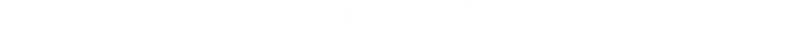
Game B

This is a little more complicated, but not much more. Again we work out the probability of failing, and subtract this from certainty. From 1.0 we, first, subtract the probability that we get no sixes in the twelve dice, then subtract the probability that we roll exactly one six.

All combinations of outcomes left have two (or more) sixes in the solution. Expanding out the binomial coefficients allows the formula to simplified.

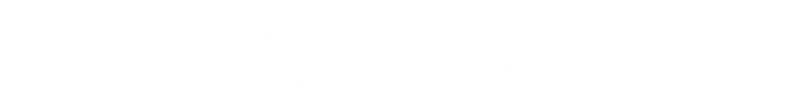
Game C

Finally, we can apply the same logic for the last game. We start out from certainty, then subtract the probability that we get no sixes in the eighteen roles (a fail), then subtract the probability we get just one six in the eighteen roles (also a fail). Finally we subtract the probability we get exactly two sixes in the eighteen roles. As before we can clean up the binomial coefficients as the numbers are so trivial.

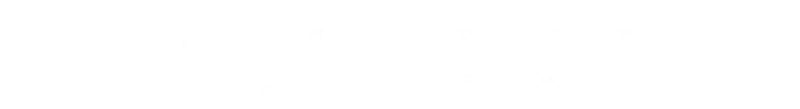
Plugging in the value of p = ¹/₆, we get the following answers:

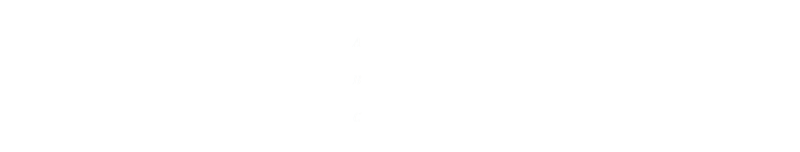
You can see that Pr_A > Pr_B > Pr_C

Newton was right, and Pepys was wrong.

Unfair Dice

What happens if we use a biased set of dice? Below is a graph showing the probability of each game winning against a varying value for p. The x-axis represents the probability of rolling a six (how biased the die is), and the y-axis shows the probability of winning the game using this die.

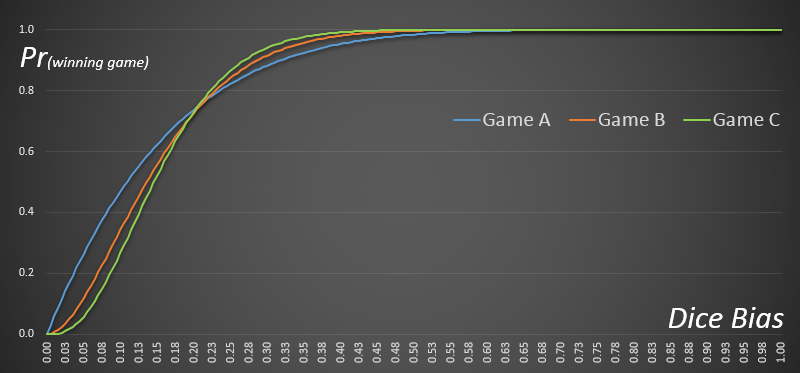
As you can see, when the probability of the die rolling a six is low, so is the probability of winning any of the games. The ranking is initially the same as with an un-biased die. However, as the die bias increases, the ranking of the games inverts, and with a highly biased die the games where more dice are rolled are more likely to win. (This aspect highlights Newtons logic error in explanation if you read his correspondence with Pepys, even though he calculated the answer correctly).

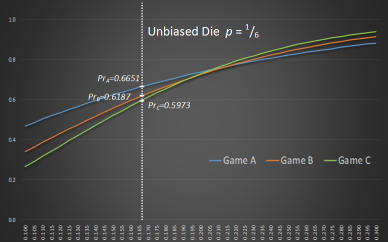To the left you can see a zoomed in part of the graph showing the region around a fair die.

If you like reading about dice puzzles, you might like the following other articles:

Sicherman Dice (How to cheat at Craps)

Intransitive Dice (How to win free drinks from friends)

Yahtzee (What is the probability of rolling a Yahtzee?)

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.