
	Advertisement

The Fallacy of The Gambler's Fallacy

Many gamblers are superstitious. They partake in predefined rituals before placing bets. Some have ‘lucky’ items of clothing they must wear. Some refrain from shaving, or carry a lucky charm, chip or coin. Many will not count their money at the table, or will not enter a casino through the main entrance.

It’s easy to see where these superstitions come from. When players have temporary periods of good or bad performance (luck), they examine their surroundings and try to project and see what could be ‘responsible’ for this deviation. If they were wearing the same shirt both times they were lucky, then surely it has to be the shirt that gives them this luck?

If they think it is unlucky to whistle when sitting at a poker table, and do it, and lose, this reinforces their beliefs.

There is science in this, but not what the gambler thinks. Gamblers with superstitions are falling victim to what psychologists call ‘Selective Amnesia’. What this means is that gamblers are only remembering events that correspond and reinforce their personal beliefs. Conversely, their brains ignore or defocus events and outcomes that conflict with their philosophy.

Physically, there is no science behind lucky superstitions. A roulette ball has no idea what color underwear you are wearing. Whether you shaved or not has no impact on how someone rolls a pair of dice at a craps table. The entity that shuffles a deck of cards has no concept of what shirt you are wearing, or if you ate cheese for breakfast!

“I used to be superstitious, then I heard it was unlucky, so I stopped!”

Conservation of Luck

Another common misconception of gamblers is the concept of ‘conservation of luck’.

Somehow they feel that the Universe needs to balance out. One way this manifests itself is a belief that the probability of future events is distorted by results in the past. You’ll hear them say things like:

“This roulette wheel has landed black lots of times, so it’s overdue to come up red!”

“I’ve flipped a coin ten times in a row and it’s come up heads each time. It’s more likely to come up tails on the next flip because of this!”

I’m sorry, but these comments are just garbage. Why should events in the past influence events yet to happen? In the coin example, just before you flip it for the eleventh time if I shout “Hold on, flip this coin instead”, and hand you a replacement coin. Will that now change the odds of you getting eleven heads in a row? (If I told you that this replacement coin had just been flipped ten times before and come up tails each time, would this change your mind yet again?)

What if I’d flipped the coin ten more times, wrote the answers individually on pieces of paper, shuffled them, and asked you to select from these papers? How could the unseen pieces of paper be re-written based on the order you selected the others in?

What if, instead of head and tails, the coin was labelled 'red' and 'black' and I had a pre-computed look-up table that converted the red/black sides to head/tail answers? This look-up table could have been created weeks before we decided to even flip the coin.

Also, how far back a window are you going to arbitrarily look to determine how things need to balance out? If the last ten flips were all heads, would you change your answer if I informed you that I’d secretly recorded the last 100 flips of that coin and that it had come up tails 70 times? According to your logic with this information, on average, now heads is the more likely answer again! If I’d recorded 200 flips, and the prejudice was flipped the other way, what would your answer then be?

The concept that past performances influences future results in a conservation of luck way, whilst appealing, is complete and utter garbage. In fact, I’ll go further and prove that, if you follow this doctrine and belief, you are more likely to lose more money.

I’ll try and use math to show that, ironically, a conservation of luck strategy is the antithesis of the strategy you should be adopting! Scientifically, you’re better off betting against the conservation of luck doctrine! Let’s see why …

A Perfect Coin

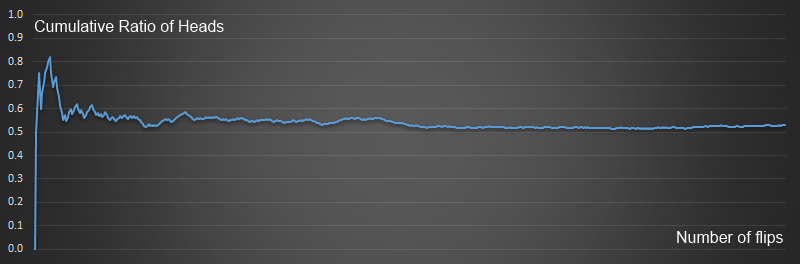
A perfectly symmetrical coin, theoretically, has a totally unbiased outcome. It should land 50% of the time on heads, and 50% of the time on tails. As discussed above, it’s a memoryless system. The coin has no internal concept of how many times it has been flipped in the past (if at all). It has no memory of what any past results were. It is agnostic, and all flips are independent. (Mathematicians describe these events as Bernoulli trials).

Sure, there is randomness. But over time, with a large number of trials, these things settle down. Below is an example graph showing flipping a coin 500 times. The x-axis shows the number of flips, and the y-axis shows what percentage of the outcomes are Heads. You can see that, over time, the graph settles down to the an expected value of near to 0.5

A Biased Coin

Let’s imagine that, rather than being perfect, our coin has a bias. This bias could be large, or it could be very small, either way, let's define it. If a regular coin has a probability of landing on heads as p (in our case p = ¹/₂), let’s define this bias with the symbol β.

If the bias is in the favour of flipping a head we can define the probabilities of flipping a head or tail with this coin as below:

Below we can see the how the expected outcome of a flipped biased coin changes over time. As before I've flipped a coin 500 times and plotted the cumulative percentage of times the coin landed heads. You can see this in the plot of a biased coin (in this case, the bias gives an expected outcome over many flips as approx 0.7)

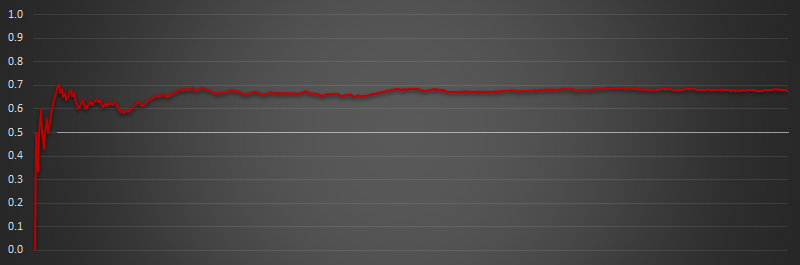
A biased coin, over a large number of events will, by definition, reveal its expected outcome. Any single flip will not reveal the true nature, but over time, a biasing of the results might indicate a biased coin.

As you see from this, if there is a strong sequence of heads in previous flips this could be an indication of a biased coin (in favour of heads). Knowing this, it is in your best interest to bet with this bias. You are more likely to guess correctly if you bet heads again after a long sequence of heads (if the reason for this is a biased coin).

This is the total opposite of the what someone following a 'conservation of luck' strategy would do!

How much advantage does this give?

If you knew what the bias is, and betted with it, how much of an advantage would this give you? We can calculate this with the expected value. We take the probability you will win, and subtract from it the probability you will lose.

We know that, for a coin, p is ½, so this reduces to an advantage of 2β in a single toss. Over n bets, you might be expected to win 2βn

What if you don't know about the bias?

Suppose you don't know if a coin is biased, what should you do?

Well, if the coin is perfectly fair and unbiased it does not matter what you do! Whatever you say, and whatever 'strategy' you employ, you have a 50:50 chance of guessing the state of the next throw!

But what if the coin is biased? You want to use this information to your advantage. If you don't know the details of this bias you can look at past behaviour.

What if we look at the last result? If the coin is biased, it is more likely to land the same way again (the bias on the first flip being the same on the second flip). What advantage does this give us?

Using this strategy, if the two tosses are HH or TT you win, and if they are HT or TH you lose. The probabilities for winning and losing are then:

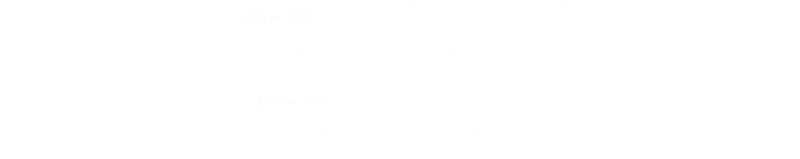
The expected outcome is the probability of winning subtract the probability of losing:

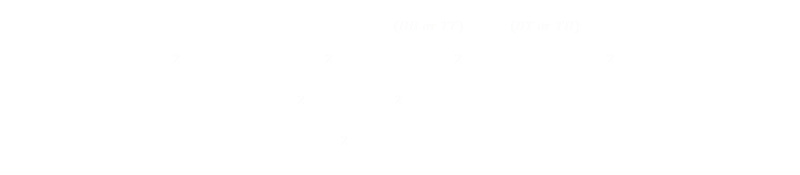
So, after n tosses of the coin, if turns out to be biased, by simply repeating the call of the last result, you can expect to gain 4nβ²

Even better

Of course, a better strategy still is to count as many previous throws as possible. I'll not go through the math, but I hope you can appreciate that the more observations you are able to get on the coin, the better your estimate of the bias is. The optimal strategy is to keep track of all previous results and simply to bet of the most popular result seen to date.

This 'voting with the majority', if taken over a large number of flips, will get closer and closer to the expected 2βn calculated earlier.

Conclusions

Of course you can't be sure if a coin is biased or not, but you've nothing to lose if it is not, so you might as well assume it is. Educate yourself with as long a history as possible of previous results and then bet that way. This is the total opposite of what The Gambler's Fallacy suggests. I hope you now see why it is called a 'Fallacy' …

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.