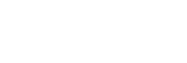
	Advertisement

Hiding from monsters

How do you avoid being shot by a laser-gun armed monster (who is riding on a train) by hiding behind a Corinthian column?

As my regular readers will know, we’ve been having ongoing monster troubles. First we had to escape the monster using a rowing boat (with the aid of calculus). Then we had to use our knowledge of Josephus to avoid being turned into the monster’s soup.

Now the monster has armed himself with a laser gun. He still wants to kill you and eat your brains.

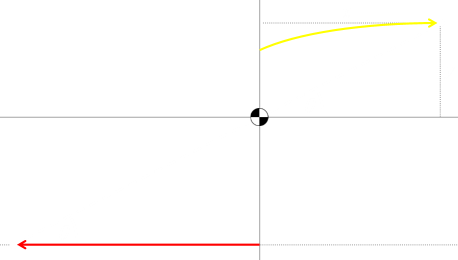
Today, the monster is riding on a train. He’s looking for you, and is hungry. The train is traveling East to West. It’s currently traveling in a tunnel and is about to exit into the open.

The monster purchased a laser gun online and is keen to use it. Being a monster he has complete 360° periphery vision, and infinitely fast reflexes. If he sees you, even for a fraction of a second, you are dead.

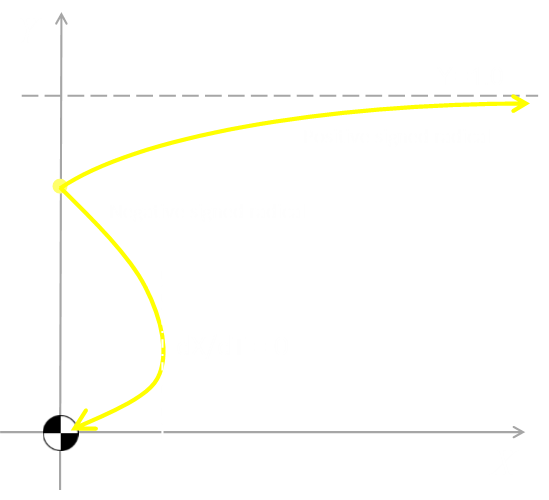
Currently, you are standing North of the exit of the tunnel.

In-between the mouth of the tunnel and where you are standing is a Corinthian column (complete with an Aspidistra plant ontop “Gronda! Gronda!”)

This column is hiding you from the murderous glare of the monster; he can’t see you.

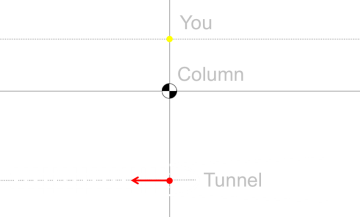
The train is traveling from East to West at a constant speed of V_M. If you stay still, as the train moves, the column will no longer hide you. Your location will be compromised, and you will be shot.

So, you need to move too. If you move correctly, you can keep the column between you and the monster. You also move at a constant speed, and we'll call this speed V_P.

The train is moving from right to left, so you need to move from left to right.

We'll define the perpendicular distance from the column to the tunnel mouth as b

We'll define the perpendicular distance from the column to your starting position as c

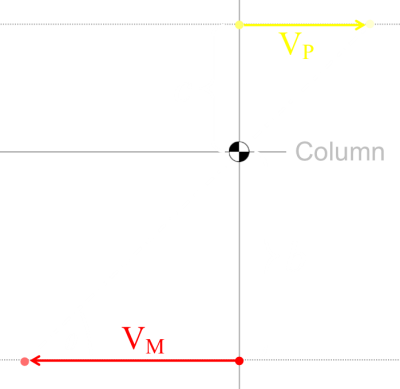There is one very special case, and this is when you can run in a straight line too. This is depicted in the diagram to the left.

After an interval of time t the train has moved a distance of V_M.t, and you will have moved a distance V_P.t

Through similar triangles we can say that:

Rearranging here is the speed you must run:

If your speed matches this exact criterion, your path will be straight. If your speed is higher or lower than this ratio, can you remain hidden? If you can evade death, what is the shape of the path you will run? Calculus is going to help us again …

Calculus

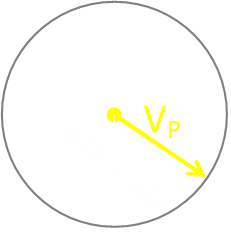
A little thought experiment tells us that, if our speed does not match the ratio defined above, that there are two possible paths that we can elect to run. We can see this in the diagram below.

At time t the monster is at position M_t

After a short time interval Δt it has moved to M_{t + Δ t}

The distance the train will have moved is V_MΔt

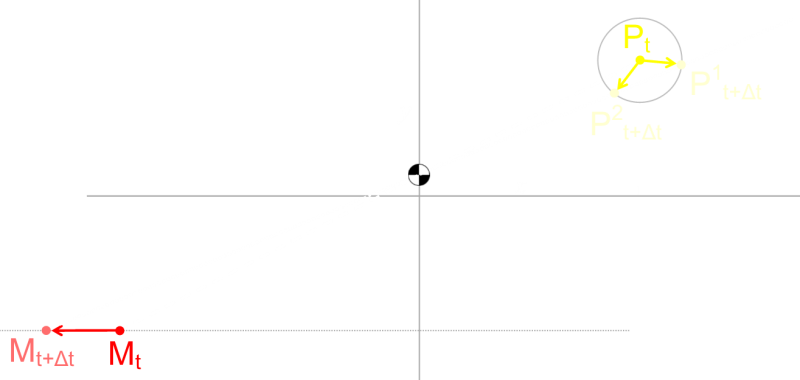
In this same short time interval, you will have moved from position P_t to your new location.

Because your speed is V_P you will have been able to travel to anywhere on the circle of radius V_PΔt

To remain hidden, we need to ensure we move to a location that is on the projected straight line that passes through the monster position and the column. As we can see, there are two possible solutions: P¹ and P²

One of these solutions moves you closer to the column, the other further away.

NOTE You can also see here that if you are not able to run at least a certain speed, there is no way you can live! There is a critical ratio of speed (depending on the geometry) that you must be able to exceed to stay alive. (A low speed for you would mean a small diameter circle in the above diagram. If the circle is too small, there are no places where it will cross the projected line passing through the column, and so you will be exposed!)

This critical speed for you is based on both the speed of the train and the geometry of the relative positions. Again, from intuition, if you are standing a long way (relatively) away from the column, you will need to move a large distance to keep the monster blocked from view. If you are close the column, not very far.

Calculus is the study of change. To work out our path we reduce the time period Δt until it is infinitely small, and use this to define the path we we travel.

We'll define two new variables to help us with our analysis. These are x and y which will describe our current position from the origin of the column.

Using geometry, at any instantaneous instant, we can define the angle from the column based on the current x and y coordinates, and using similar triangles again, relate this to the position of the monster.

This can be re-arranged to this:

Then differentiated with respect to time:

Using Pythagoras, we can describe the relationship between the instantaneous velocity V_P and the x and y components:

Combining these last two equations results in this:

Expanding this out and a little bit of algebra reveals this important result (equation A):

This is starting to get a little unwieldy, so let’s introduce some new terms, these are X, Y and T.

These are (dimensionless) terms. These are ways to represent the spatial coordinates as the function of the ratio of the two speeds over the distance between the column and the train track.

Through the application of the Chain rule to the middle equation above, we can create another important result (equation B):

Combining equation B and equation A, and using the substitutions for X, Y and T gives this result (stick with me, it’s downhill from here).

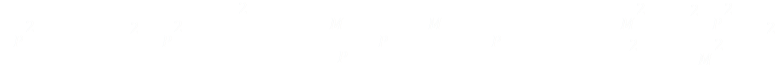
Lot's of things cancel and simplify. We can re-arrange to get into a quadratic equation of ^dY/_dT in standard form.

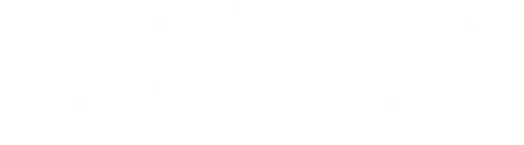
Through the application of the quadratic root formula we can solve this equation. Here is our result. This importnat equation shows the relationship between Y and T

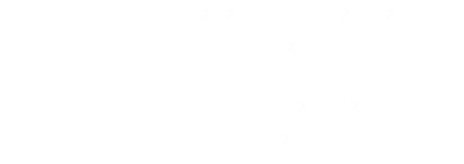
Halfway there

Now we need to find the relationship between X and T. Recalling back to our normalization definitions, and the similar triangles, we know that:

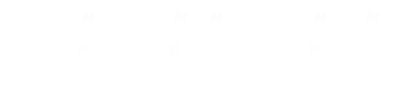
Differentiating YT with respect to T we get:

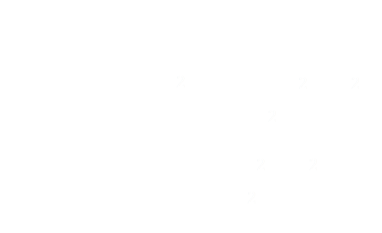
What can we learn from this?

We can immediately see from these equations that there are two roots, and the ± infront of the square root symbol defines these. This confirms our thought experiment where we predicted the two solutions (where the circle intercepted the line of sight in two locations).

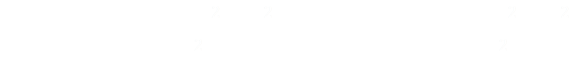
What else can we infer without solving these equations? Well, first we know that the solutions to these these equations are real, so the value in the square root must be ≥ zero. This means that (1+T²) ≥ Y²

When we start T=0, so we know that Y ≤ 1 (at the start of the 'race') to keep the square root positive.

We also know from the definition of Y (the normalised equation), that all the values in the dimensionless ratio are positive. Thus, it can never go negative. We now know that 0 ≤ Y ≤ 1

And we're off …

When we start T=0, we know our initial start position, y=b. Plugging these values into the definition for Y and we know that this is ≤ 1.

This shows us another important piece of information:

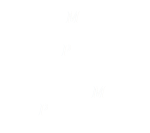
To survive you need to be able to run at least as fast as V_M(c/b), otherwise you are toast*

*Or however the monster elects to prepare your laser blasted corpse!

If we set ^dY/_dT = 0, we can see this can only occur when Y = 1. Plugging this into our normalized definitions and this corresponds to the straight line solution. A nice piece of validation. (Students of Calculus can research Picard's Method and learn that at no time can Y exceed 1, because it is a unique solution).

Non-trivial solutions

If the starting conditions are not the special straight line solution, as we know that the ± components and our thought experiment, shows we have two solution paths. We know one solution moves us closer to the column and one further away. (Another exercise for eager students is to show that, for the positive sign root, the value for Y monotonically increases (bounded at 1.0), and for the negative sign root monotonically it decreases).

If you elect to take the path that moves you closer to the column, eventually you'll get there! (after passing through an inflection point in the x direction where you reverse direction in the axis).

This inflection point occurs when the denominator, above, is zero.

When you reach the column you can spin around it in whatever direction you like, maintaining a safe hiding position until the monster's train passes out of lethal range.

Can't make up your mind?

The above solutions show the curves that are obtained if you decide on a run strategy (towards or away from the column), and stick to it. But of course there is no reason to do this!

At any time (providing your relative speed is above the toast ratio), you can switch between the two strategies at will. You can vacillate to your heart's content; changing between the move towards or move away strategies and still keep hidden from the monster.

Let's look at some of these potential paths. In the diagrams below, the y-axis shows the normalized value Y ranging beteen (0.0 - 1.0) The a-axis shows the value X ranging beteen (0.0 - 2.0). To make the charts easier to understand, I've used the color red to depict paths moving away from the column, and the color blue to show the paths moving towards from the column.

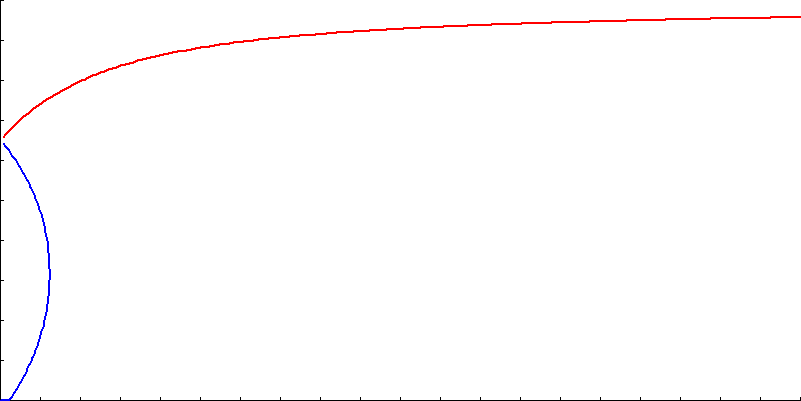
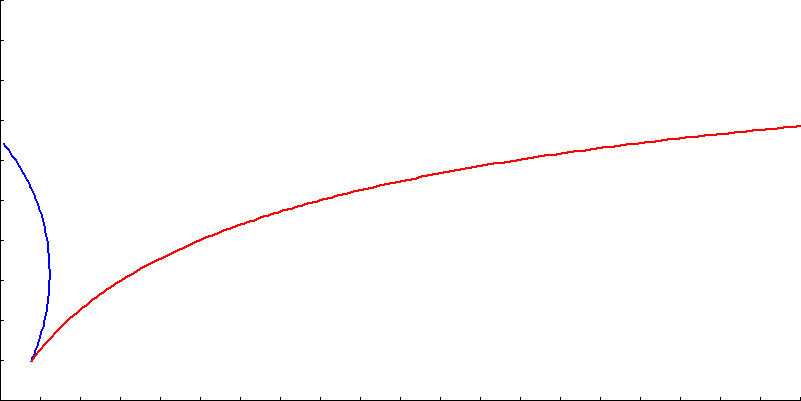
Below is a chart of both paths, starting a Y = 0.65, and sticking the chosen strategy. The red path asymptotes to 1.0, and the blue path reaches the column.

Here is what happens if, starting from the same starting position of Y = 0.65, we switch between the two strategies of moving towards and away from the column (at regular intervals). In the first plot, we initially run away from the column …

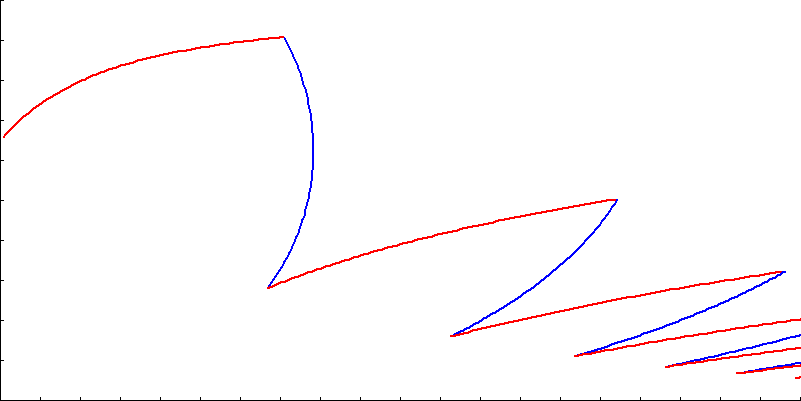
Here is the same start position, but this time, this is the path we follow if we initially move towards the column. Note - In this simulation, to avoid issues with numbers going negative, rather than overshooting, I simply truncate each component to zero, individually, if this were to occur.

Here are a couple of paths obtained by switching at random:

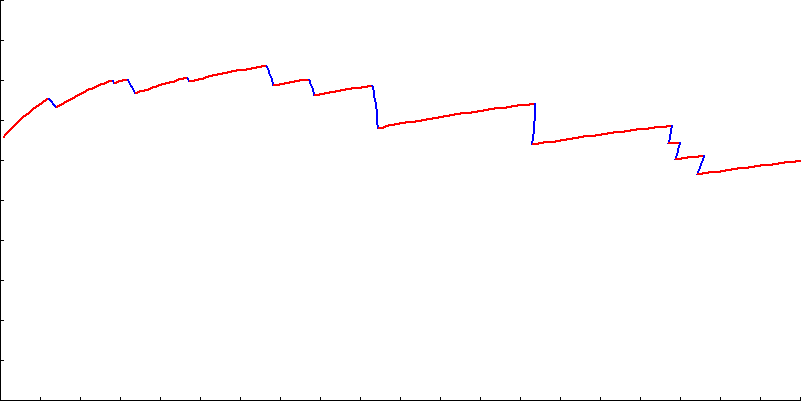
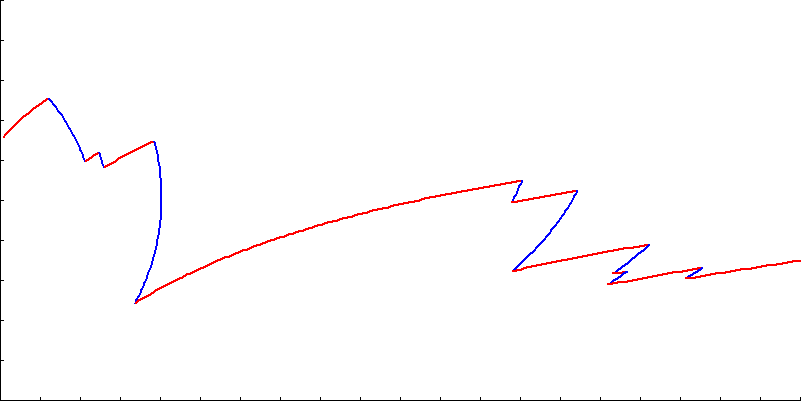
Finally, here are the paths obtained if we switch strategies when we get to 10% of either boundary (0.1 ≤ Y ≤ 0.9). First starting moving away, then starting moving towards.

Escape Successful!

Yet again we've avoided the monster, congratulations!

(If you want a recap of our previous encounters, see here and here).

I wish all my readers a Happy (and monster-death free) New Year!

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.