Dark Dilemma
 |
“He’s at it again!” You’ve successfully avoided being eaten by a monster three times now (Lake Escape, Soup Escape and Column Escape), but the monster still wants to dine on your brains. He’s captured you again. |
|
Whilst he is thinking of how best to eat you, the monster has cuffed your hands together, and dragged you into somewhere near the middle of what appears to be a very large windowless room. He gives the key to the handcuffs to a nearby rat (don’t ask me why), and the rat proceeds to scurry away with it. As you watch the rat run away, so do your hopes. If only you could get the key. If you had the key, you could un-cuff your hands and, knowing that you can outrun the monster, easily escape. |
 |
 |
Just as you are watching the rat, suddenly all the lights go out! It’s now pitch black; this is your chance to escape! You know where the rat was the instant the lights went out, and you know that you can run faster than the rat. |
|
You also know about rats. You know that the rat, once the lights go, will select a new random direction to run, and will continue to run in a straight line on that new heading. This direction could be directly towards you, it could be directly away, in fact, it could be any direction at all. All you know is that, once the rat selects his direction, he’ll continue in that direction. |
 |
Impossible Problem?
Your only chance of escape is to catch the rat and get the key.
Which way should you run? Knowing that your hands are cuffed, your only chance of capturing the rat is to be right on top of it. The rat runs as quiet as a mouse <sic>, so you’ll not be able to hear it, and it’s pitch black, so you’ll not be able to see it. You’re going to have to collide with it, pin it down with your body and liberate the key to make your escape. But how can you do this if you don’t know which direction he will run?
 |
At first glance, this seems like an impossible problem. Surely you'll only be able to collide with the rat by sheer luck? Surprisingly, there is a solution. There is a path you can run that guarantees you will collide with the rat (irrespective of the direction the rat elects to run). Let's work out what that path is. Yes, it’s time for some more calculus … |
Definitions
Here are some definitions we'll use to help us with this problem:
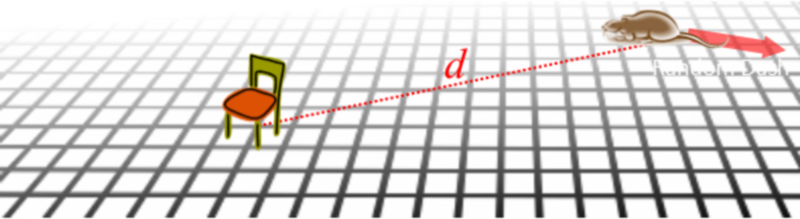
We'll define the distance between where you stand and where the rat is when the lights go out as d
The (constant) speed that you can run whilst cuffed is SY
The (constant) speed that the rat runs is SR You can run faster than the rat (SY > SR)
We'll use the variable t to represent the time elapsed since the lights went out.
We'll use a coordinate system to help us describe the paths you and the rat travel, and we'll define the origin of this coordinate system to be the position of the rat the moment the lights go out. We'll use θ to represent the angle of a position vector from this origin.
And whither then? I cannot say
The key to determining the solution is to realize that, at the point of capture, both you and the rat are the same distance from the origin. We know the rat starts at the origin, and travels in a straight line at constant speed. At time t, the collision point must be SR.t from the origin (in some unknown direction).
So, to solve the puzzle we need to ensure that you run to a place that is a distance SR.t from the origin too (but this could be in any direction). The key is that we don't need to visit these locations all at the same time! All we need to do to solve, is come up with path that tries all of them. We can do this, because t is a variable.
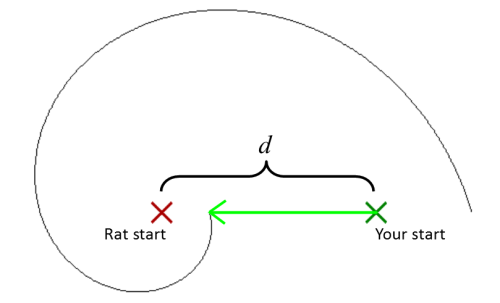 |
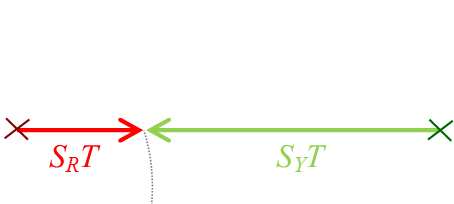
In the diagram to the left your starting position is shown by the dark green cross. The position of the rat when the lights go out is shown by the dark red cross. The first part of your strategy should be to run directly toward where the rat was (directly towards the origin). You should continue running on this path up to a point where, if the rat were running towards you, you would meet.
(This is the shortest possible time that a collision could occur; this is a trivial solution). |
If you don't meet the rat at the end of this straight run, you should start a spiralling path (centred on the origin), expanding outwards. If the spiral radius is increased over time so that your distance from the origin is the same as that of the rat from the origin, then at some time, you will collide.
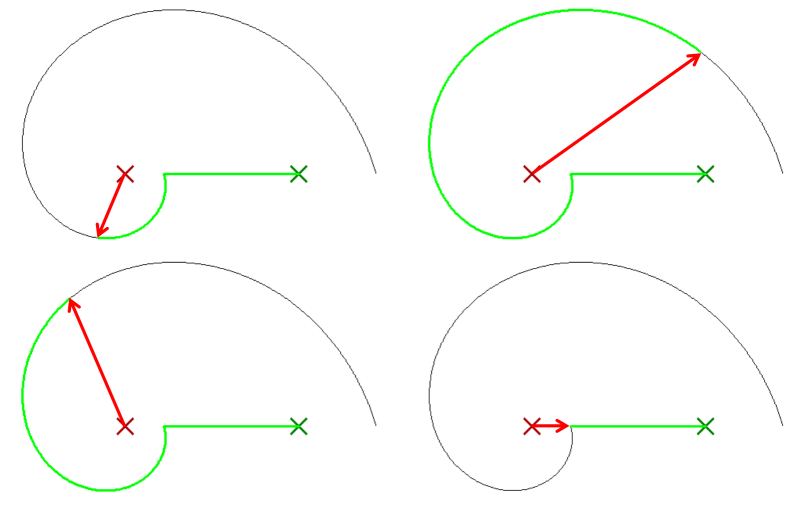
Not only is it certain that you will collide with the rat if you follow this spiral, it is certain that you collide before completing 360° of the spiral. Below are a couple of examples of possible solutions (with the trivial solution shown in lower right). The path taken by the rat is show in red and the path you would run is shown in green.
Let the math begin
The first step is to calculate the time it takes us to complete the straight line dash. We'll call this time T.
 |
 |
The starting radius of the spiral, is the same as the distance run by the rat, and this is:
If we define the position vector P at time t (at any time after time T), it can be represented by the formula below, where θ is a, yet to be determined, function of angle against time.

Substituting T, this simplifies to this (of course the modulus of the position vector should is also equal to SRt)
The velocity vector of that you run is the first differential with respect to time.
Using Euler's Indentity to expand the complex exponentials and collecting terms we get:
The speed you run around the spiral is a scalar value and this is the magnitude the velocity vector. The square of the modulus of the velocity vector is the same as the square of the speed you run.
Substituting this in we get the following hairy (at first glance), equation:
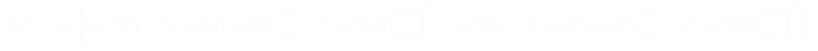
However two of the terms cancel, and the other nasty stuff collapses with a simple trig equality.
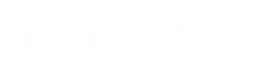
Rearranging to get the velocity vector we get this pretty little equation.

(It does not matter if you take the positive or negative sign of the radical. This just shows that, once you've completed your straight sprint, you can run either clockwise or counter-clockwise around the origin).
To get the angle (with respect to time), we integrate this angular velocity equation.
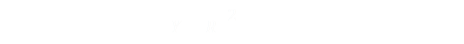
Remembering back High-School calculus we recall that if we use Indefinite Integration we need to apply a constant (we've integrated the rate of change but have yet to determine where we started). Before doing that, let's simplify things by remembering that both your speed, and the speed of the rat, are both constants too. We can combine these speed values and the radical into one constant (we'll call it λ).

Substituting in we get a, much easier to digest, equation. At the start of the spiral θ = 0, this occurs at the time t = T. With this we can determine the value for our indefinite integration constant C.
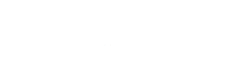
Subtracting two logs is the same as dividing the two values inside the log function. Then rearranging we have our answer. The time we'll collide with the rat is given by the simple equation below:
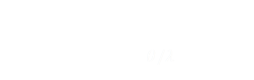
This is the relationship between the time to the collision and the angle at which it will occur. Neat!
What position will the collision occur at?
It's just downhill algebra from here. Want to know the radius that the collision will occur at? Let's call this r. We know the rat moves in a straight line from the origin at speed SR so the rat himself moves along this radius. Since r = SRt, combing this with the result above gives us the equation for t.
Expanding everything out in nauseating details give the final result:
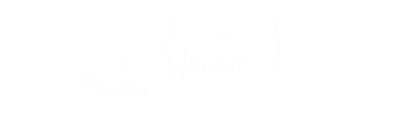
The results
Here is an animated illustration of this equation in action. The red circle shows all possible positions the rat could be. Starting at time t = 0, the circle grows. The green line shows the path you should run. You notice that as soon as the red circle touches the green line, the two stay in contact all the way around until a complete circle has been made.
Whatever direction the rat elects to run, you'll catch him!
 |
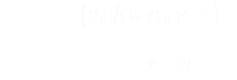
(Same formula, just re-arranged) |
Escape Successful!
 |
Yet again we've avoided the monster, congratulations! (If you want a recap of our previous encounters, see Lake Escape, Soup Escape and Column Escape). |
 |
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.


