Optimal Bucket
|
What is the optimal shape for a bucket? If you were designing a bucket, what shape would you select so that it maximizes the fluid it can hold based on the material used to make the bucket? |
 |
Tube
Let’s start out by looking at the simple case of a cylindrical tube. What would be the shape of a bucket if it had vertical cylindrical sides?
|
In a previous posting, I talked about why cylindrical cans are shaped the way they are. In summary, if a cylindrical tube is capped at both ends, then the most efficient aspect ratio is when the cylinder is of the height of twice the radius. This is the shape that maximizes the volume for the surface area. |  |
 |
Buckets, do not have lids. They are open topped. If a cylinder is open topped, we can perform a similar calculation and show that the shape that allows it to hold the most fluid (for a given surface area) is when the ‘cup’ is of a height that is equal to the radius. |
Proof:
The volume the cup can hold is the area of the base, multiplied by the height. Rearranging, we can find the height:
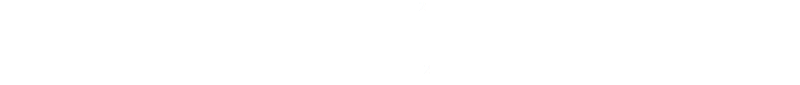
The surface area of the cup is the area of the end cap, plus the sides that wrap around. We can substitute in the equation we derived for the height to get an expression for the surface area in terms of the radius:
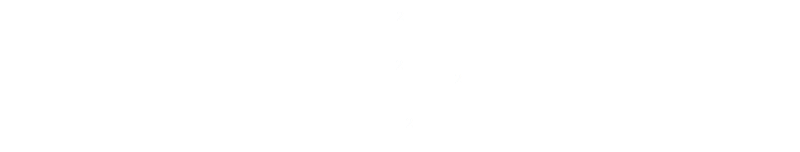
If we differentiate this with respect to the radius, and set this zero, we can find the turning point (as the second derivation is positive, we can confirm this turning point is a minimum), and this will give us an expression for the minimum surface area for a fixed volume.
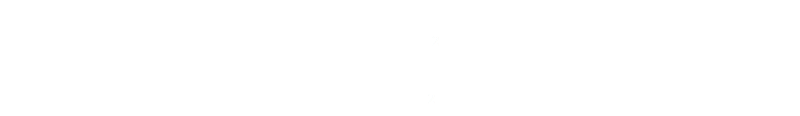
Substituting this back into our equation for the volume we can show that the shape that minimizes the surface area for a fixed volume (maximizes the volume for a given surface area), for a cup is the aspect ratio where the height is equal to the radius.
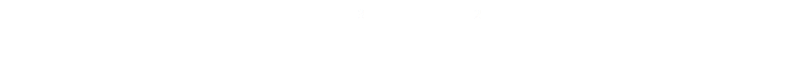
Better than a tube?
|
Can we do better? An open topped cylinder can hold a certain volume of fluid, but if we slanted the sides*, could it hold more? If we slope them out then the top of container is a larger radius, but this would require more material, and so, if we use the same amount of material, we’d be able to get less height in the bucket. *I’m only going to consider straight sided cylindrical buckets. If we allowed curved sides, the most efficient shape would be a hemi-sphere. Buckets shaped like half a grapefruit would not be very stable! |
 |
Math
What is the relationship between the height, radii, volume and surface area of a bucket?
 |
The mathematical term for a truncated cone is a circular based Frustum (More details: Frustum). The following equation describes the volume of a frustum: 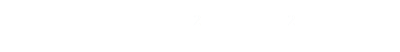
Where R is the radius of the top, and r is the radius for the base. For our bucket, the total surface area is the area of the bottom of the bucket plus the area of the sides (there is no top): 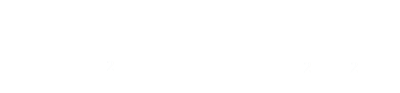
|
We can re-arrange this last equation to describe the height h of the bucket based on the two radii.
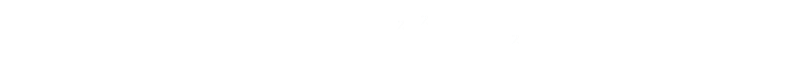
Finally we can substitute this height into the volume equation to give the following formula:

Flat Disk
If we have a flat disk of Radius R=1, it makes a pretty poor bucket, but it is an easy way to calculate the surface area, and thus a measure of the material used.
This disk has area S=πR2
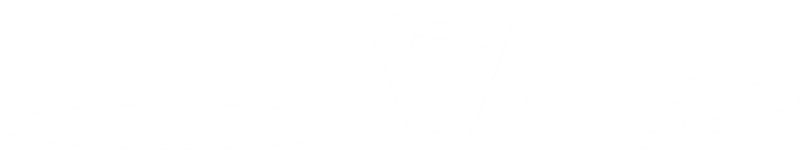
It's possible to deform this blank disk slug into a bucket shape with a bottom circular base and sides with a variety of angles. Depending on the radius of the top of the bucket the height will change.
If we keep the surface area of the bucket fixed (to that of the starting disk), for all possible attainable values of the top and bottom radius (R, r) it is possible to calculate the holding volume. Each configuration will have the same surface area (bottom + sides), but depending on the ratio of the radii, the height will vary considerably.
Each radius can be in the range 0 – 1. With either the top, or bottom radius = 1, then the bucket will simply be a flat disk and have no volume. When the bottom radius r=0, then the bucket will be a cone.

When the top radius R is greater than the bottom radius r, it's still a bucket, just not a very efficient one! With a smaller top radius, the bucket would look like a lampshade!
Results
Let's look at some results. If we keep the bottom radius to zero r=0, and simply vary the top Radius R from 0 – 1 then we get the following curve for the volume:
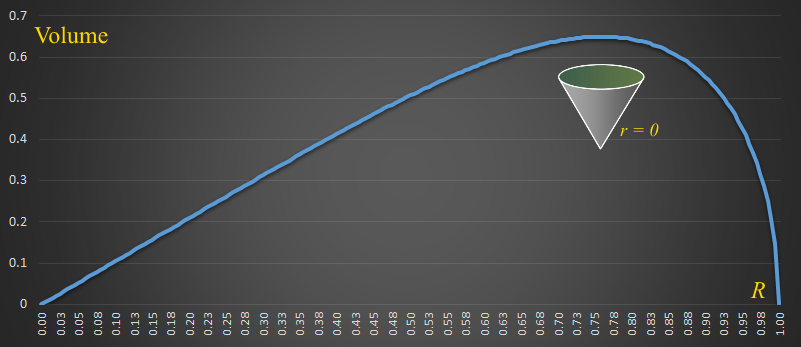
As we've kept r=0, then the shapes are all conical. As expected, when R=1 then the volume of the bucket is zero (it's just a flat disk with no holding capacity), and with R=0, it's not defined. For values in-between, as the top radius is modified, the fixed surface area defines the height, and thus the volume of the cone (as the top radius gets smaller, the cone gets taller and slender, but this becomes less efficient. Similarly, as the top radius gets larger, the shape becomes flatter and less efficient). There is a maximum value for this shape. If we were going to make the bucket conical shaped, then the optimal top radius is approx R ≈ 0.76
How do things change as we start to add a base to the bucket? Below are graphs for various values of r, from 0.00 to 0.95
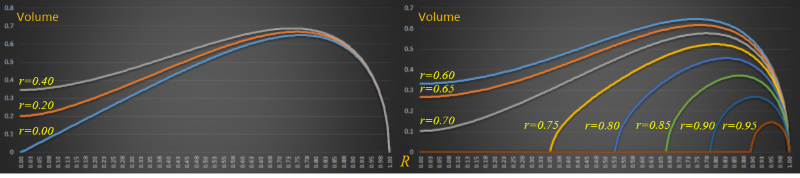
The 0.0 curve is the conical bucket we saw in the first graph. Initially, as the value for r increases (graphs on the left), the potential volume of the bucket increases. Adding a base, initially increases the carrying potential. As before, increasing R, also increase volume, up until a critical maximum.
As we increase the value of r beyond a certain point, the carrying capacity of the bucket starts to decrease. The graph on the right shows values for r=0.60 – 0.95 You can see that, as the bucket gets a broader and broader base, that the volume decreases again.
Another interesting fact is that somewhere between r=0.70 and r=0.75, a point is reached that the base becomes so wide that it is impossible to make the sides required to create a small top radius. It's only possible to make buckets with a smaller and smaller range of R for a given base. (Imagine a lampshade shape with a very wide base. The base is so large, and uses so much material, that whatever is left to make the sides is not enough to make a top radius that is very much different from the base).
What about keeping the top radius R fixed and seeing the effect on the volume?
Below is a graph showing R=0.2 and how the volume changes with different values of r:
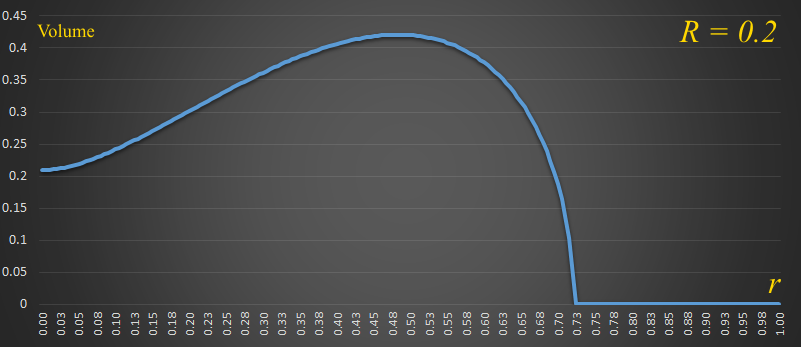
There is a value above which (on the right of the graph), that it is impossible to make a bucket because there is not enough material.
Also interesting is the inflection point on the graph where the top and bottom radius are the same (r=R=0.2) This point is where the bucket is a cylinder, and there is rotational symmetry around this point.
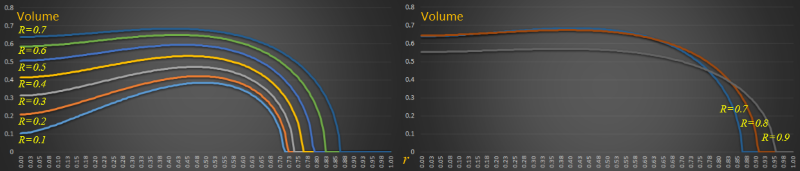
As the value of the top radius varies, so does the volume achievable over a range of potential bases radii. Below are graphs of these. On the left are a range of values for R in the range 0.1 – 0.7 You can see here with increasing top radius, over all possible values for the bottom radius, the volume is higher for any given bottom radius. The right graph shows more extreme values of R; once a certain point is past, increases in the top radius decreases the volume of the bucket.
3D plot
Since it is possible to select both the top and bottom radii, we can plot all possible valid values for R and r on a 3d graph, using the z-axis to depict volume. This allows much better interpretation of how these variables effect the outcome.
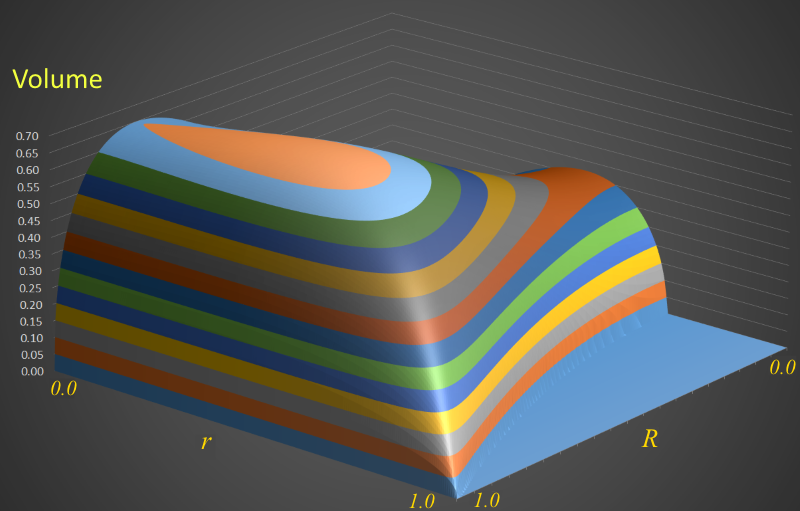
The earlier line graphs are the equivalent of vertical orthogonal slices through this plot.
For a low-resolution animated version of this 3D plot click here.
If your browser supports animated PNG format images, you can try viewing a higher resolution version.
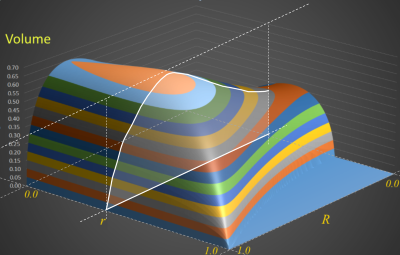 |
To the left is an example slice showing a cross-section around r=0.5 (note in this projection of the surface, zero is at the back of the axes). |
Maximum Value
|
The maximum volume of any possible bucket is the highest point on this 3D surface. It is shown on the contour plot to the right. R ≈ 0.74 r ≈ 0.41 (Where 1.0 corresponds to the radius of the flat disk). |
 |
With these values, the height of the bucket will be h ≈ 0.66, and the corresponding Volume is V ≈ 0.69 units cubed .
What does this bucket look like?
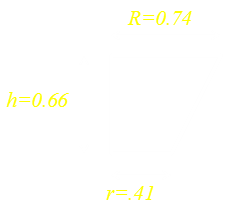 |
Here are the radii and height measurements of the coordinates of the highest volume bucket (drawn approximately to scale). |
|
This is what a bucket with these dimensions looks like. This assumes that the bucket is filled all the way to the very top (something you probably never do). |  |
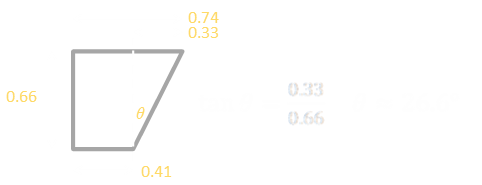 |
A little bit of geometry allows the angle of sides to be calculated. |
But most buckets don't look like this, why?
We've calculated the optimal shape a bucket should be, but most buckets don't look like this (though to be honest, it does look very similar to a breakfast cereal bowl, don't you think? Breakfast bowls have similar design criteria). Why aren't buckets shaped like this in real life?
 |
There are probably a plurality of reasons, and here are just a few: We've optimised based on material, but not cost of manufacture. This optimal bucket shape is very broad at the top making storing it very awkward (can you imagine having one that shape under your sink?). Most buckets have handles on them to allow them to be lifted and moved; a handle on this design would be wider and harder to attach to the sides. Even with a handle, carrying a bucket this shape would probably be less stable as the center of mass of the contents would be closer to the pivot point (your hand). |
Miscellany
A while ago, I wrote a similar article about Pleated Sauce Cups and how the carrying capacity of these can be increased by relaxing the pleats slightly. There is, however, a subtle difference in that calculation because with a pleated sauce cup the material is already fixed (they are manufactured as waxed paper disks, and then pleated). The pleats are folds, so there is no material 'saved'. In the bucket calculation we are using just the correct amount of material to make the desired angle sides. |
 |
 |
If you take two 'buckets', invert one, then stick it to the top of other other, if you do it correctly, you'll get a barrel. I know we restricted ourselves to straight edges in our simple calculation, but you can start to see the similarity in shape between a barrel and two buckets. (Again, I'm over simplifying things and there is a compromise between making the most efficient container for the volume against manufacture, storage and stability. If you make barrels too wide in the girth then, when you store them side-by-side, there is a lot of 'wasted' space between them). Having a bulge in the middle also makes a barrel, not only easier to roll, but significantly easier to manoeuvre and change direction when rolling. Can you imagine rolling a full cylindrical oil drum and trying to change the direction of that? |
Trivia
A person who makes barrels (and also kegs, wooden buckets, firkins and other such containers), is called a cooper.
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.

