Our atmosphere
Our Earth is surrounded by a thin blanket of breathable gas. We call this our atmosphere. Without it, there would (probably) be no life. Amongst many things, our atmosphere contains the oxygen we breathe, the gases we exhale (that the plants and trees then use), and water vapour that creates our precipitation. It protects our planet from cosmic rays and all but the largest of meteors.
 |
The atmosphere keeps our planet warm, and buffers us from becoming too hot or too cold. It produces winds and weather to circulate and mix everything around. Whilst it’s easy to think of air as ‘weightless’, this is not true. The air we breathe has very measurable mass*, and it’s this mass, and gravity, that keeps it attached to our planet! |
It might surprise you to learn that air, actually, is quite a lot heavier than you think. On the surface of the Earth, at sea level, you are standing at the bottom of an entire ocean of air. The force of all the air above your head pushing down creates pressure.

5,000,000,000,000,000,000 Kg |
*The total mass of air in the atmosphere is approximately 5 quadrillion metric tons! That’s about one millionth of the mass of the rest of the planet. |
Pressure
 |
Pressure is the measure of Force per unit area. The average atmospheric pressure at sea level is 101,325 N/m2. (One Newton per Metre Squared is given the unit One Pascal, after the French physicist Blaise Pascal). For my non-metric readers, this is approximately 14.7 pounds over every square inch (PSI). If you have a table, at sea level, which is 1m2, the weight of the air above it pressing down is equivalent to the weight of about seven compact cars! That's an awful lot of weight. |
|
So, why doesn’t the table collapse? Well, the simple answer is that the pressure applies in all directions. It’s not simply the force on the top of the table pressing down. There is air, and air pressure, on the underside of the table pushing up, and the two forces cancel.
|
 |
States of matter
We’ll pick up with air pressure again in a minute, but first let’s take a little diversion into what exactly air is. Air is a gas (more specifically a mixture of gasses: approx. 78% Nitrogen, 21% Oxygen, and the rest Carbon Dioxide, water vapour, and trace amounts of mainly noble gasses).
Gas is one of the four distinct states (phases) that matter can exist in. The others being: Solid, liquid and plasma. (I’m ignoring, on purpose, the extreme other phases, such as Bose-Eintstein condensates, Quark-gluon plasmas …)
Discounting plasmas (which only occur at extreme temperatures and are, physically at least, a gas-like cloud), the three states: Solid, Liquid, Gas have distinct physical properties.
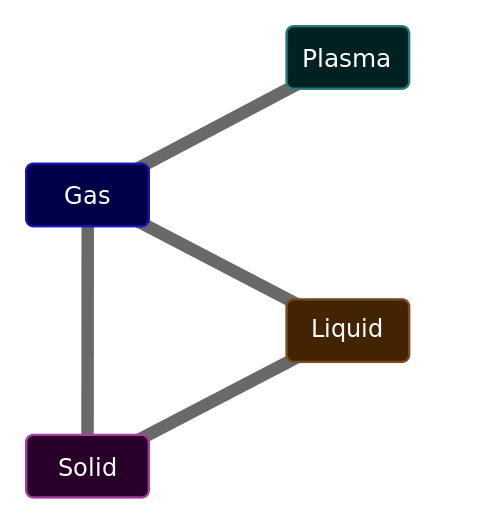 |
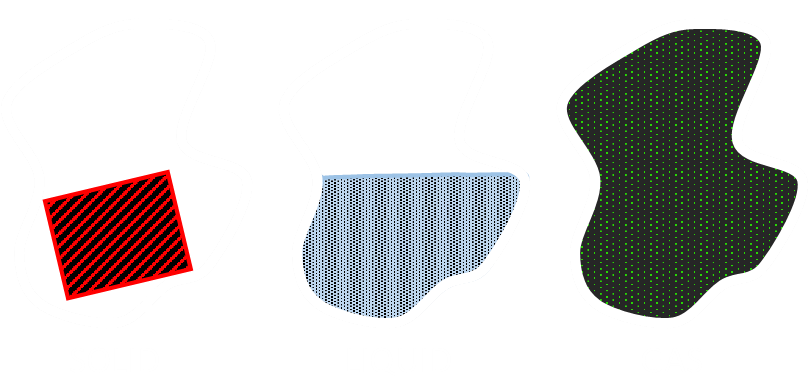
Solid – A solid has very little space between its constituent particles. The particles are tightly packed; often in a regular pattern. It is not easily compressed. It retains both volume and shape. Its particles do not flow. If it were placed in an irregular shape, like the example below, it would keep the same form. Because its particles are close together, solids (and liquids) are often called condensed states of matter. Particles in a solid can vibrate, but do not generally move around. Liquid – The particles in a liquid are close together, but are not in a regular arrangement. Particles can slide easily over one another. If placed in an irregular container, it will arrange itself to conform to (part of) the shape of the container, but it’s volume will remain constant. Like a solid, it is hard to compress. Particles in a liquid move about and mix. Gas – The particles in a gas are well separated with no regular arrangement or structure. They move at high speed and freely. They expand to assume the shape and volume of the container they are in. Because there is a lot of space between their particles, they are compressible. The diagram on the left shows the relationship between these phases and the common names given to their state transitions. The higher up the chart, the higher the enthalpy of the system (the amount of energy at a constant pressure). |
(In a plasma, the particles are so energetic that they break up into a soup of positive ions and free electrons. Whilst not common on Earth, the vast majority of matter in the visible universe is in the plasma state.)
Back to the atmosphere
 |
Pressure of the atmosphere at ground level is at its highest. Air at ground level has the entire weight of all the particles above acting on it. As you move to a higher altitude, there are less molecules above and this results in less force and less pressure. The air pressure at the top of a mountain is lower than at sea level. The air pressure where an airliner typicaly cruises is lower still. Because air is gas, it is compressible. The density of air decreases (as does the pressure) as the altitude increases (there is less weight above squashing it down). Airlines cruise as high as possible because the lower density of the air results in a lower aerodynamic drag. The higher a plan can fly, the more efficient it becomes. The higher and higher altitude, the lower and lower the density becomes. Whilst, mathematically, this could continue decreasing forever, getting infinitely smaller with no abrupt edge, a cut-off of point is defined. This cut-off line is given the name the Kármán line*, and it occurs at an altitude of 100km. Beyond the Kármán line, you are in space. |
|
Any person who obtains an altitude higher than the Kármán altitude can officially call themselves an astronaut, according to the Fédération Aéronautique Internationale (at the time of writing this blog, just over 500 people). In the US, however, professional, military, and commercial astronauts who travel above an altitude of 50 miles (80 km) are awarded their astronaut wings. For comparison, modern airliners cruise at between 33,000ft – 43,000ft, which is just 10km – 13km. 99.99997% of the mass of the Earth’s atmosphere is enclosed below the Kármán line. |
 |
 |
*The Kármán line is named after a brilliant Hungarian aeronautical engineer called Theodore von Kármán (1881-1963). He calculated that, above this line, air becomes so thin that, in order to support aerodynamic lift, the velocity needed would be so high that it would exceed orbital velocity at that altitude! He is also famous for making the following true, but honest in a brutal way, statement: |
“When you are talking to technically illiterate people you must resort to the plausible falsehood instead of the difficult truth.”
|
As you can see, space isn't very far away at all. As astronomer Fred Hoyle once said, “Outer space is not far at all; it's only one hour away by car. If your car could go straight up!” |
 |
Deriving the relationship
To calculate how pressure changes with altitude, we need a little calculus. We'll do this in two stages. First we'll make the approximation that the temperature of the atmosphere is constant (iso-thermal). After we derive the basic relationship (which turns out to be pretty good), we'll modify our formula to take into account the issue of temperature variance.
 |
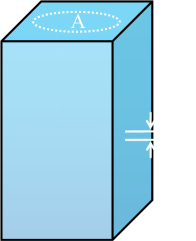
First we’ll imagine a column of air, starting at the ground and rising up to the infinity of space. This column has a cross-sectional area of A It’s composed of a series of infinitesimally thin slices of height dh We’ll define the origin as ground level, and the altitude of each slice as h from this origin. |
When the column of air is in static equilibrium, the weight of each thin slice of air is balanced by the pressure difference between the bottom and top of the slice.
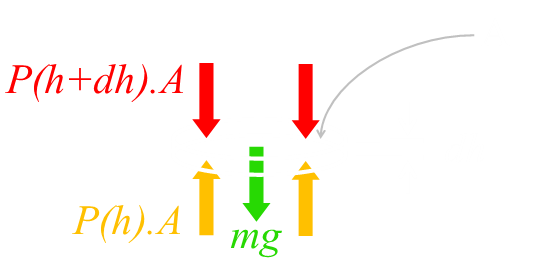
The mass of air in the slice is the density of the slice multiplied by its volume. Resolving forces gives this equation:
Re-arranging results in this simple equation:
The density of air is not constant, however, and varies with Pressure, so we need to know the relationship between these. The Ideal Gas eqaution is our friend, and we can relate the Pressure to density using Temperature (T), the mass of the air molecule (m), and the ideal gas Boltzmann constant (k).
Inserting the formula for ρ to the differential equation for Pressure and height allows to to be easily solved.
Plotting this equation we get a curve like the one shown below. On the x-axis is pressure measured in atmospheres. On the y-axis is altitude (measured in Meters).
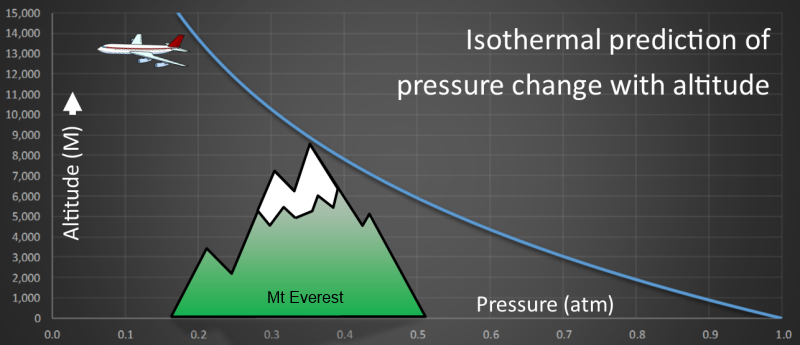
We can see that pressure reaches half sea-level pressure at approximately 6km altitude using this model.
Lapse rate
The above isothermal model assumed that the temperature of air did not change with altitude. We know this is not the case. Temperature decreases with altitude. We can model this with something called a lapse rate. This defines how the temperature decreases with altitude. If we assume a linear lapse rate, we can represent the temperature as a function of altitude using this formula:

Here T0 is the temperature of the air at sea-level, and β is the lapse rate. (In the lower atmosphere, air reduces in temperature approx 6.5K per 1,000m).
Here is the differential equation for the pressure we derived earlier.
Substituting the temperature lapse rate approximation into the differential equation we can work on a formula for estimating the pressure with this new constraint.
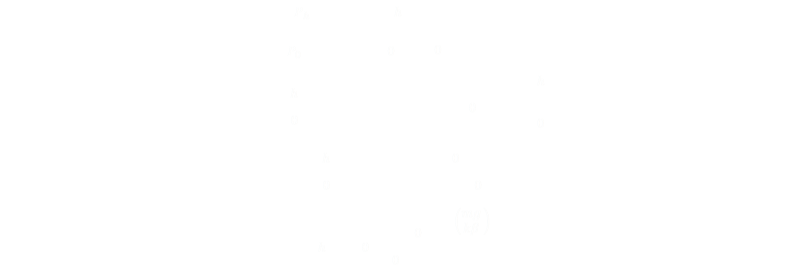
Here is a comparison of these two approximations using average real-world values for the temperatures and lapse-rates. As you can see, at lower altitudes, there is very little difference. As the altitude gets higher, the isothermal model over-estimates what the pressure will be.
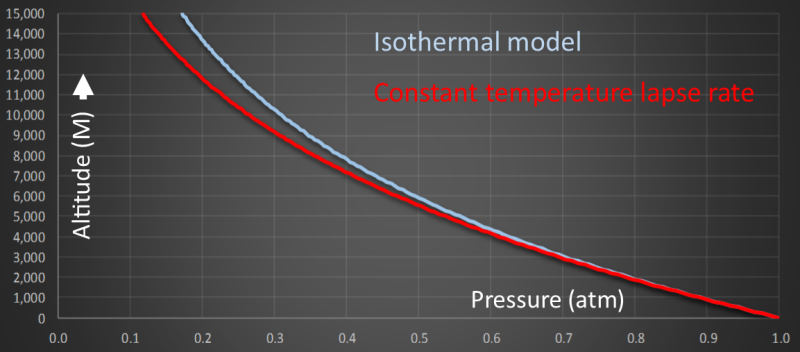
Real Atmosphere
In reality, the atmosphere is neither isothermal, nor is there a constant lapse rate. Our atmosphere is stratified into a series of distinct layers; each with it’s own temperature lapse rate. These layers, however, do have reasonable temperature linearity within each layer, and a fairly good model can be obtained by applying the linear lapse rate approximation over each layer distinctly like a giant layer cake.
The major layers of the atmosphere are:
Troposphere – The Troposphere contains approx 80% of the mass of the atmosphere, and extends up to an average altitude of 12km. Most of our weather occurs in the Troposphere. The air in the Troposphere is heated mainly by reflected energy from the ground. This is why it has a negative lapse rate; the further away from the ground you get, the less influence the Earth has on the air temperature.
Stratosphere – The Stratosphere extends from the top of the Troposhere (the Tropopause) up to approx 50km. It contains some of our high clouds, but not a lot of our weather. It is heated mainly by ultra-violet solar light from above. A consequence of this is that its temperature increases with altitude. Whilst at the Tropopause it can be very cold (below -60°C), the temperature can increase to close to freezing point at the Stratopause (the boundary with Mesosphere)!
Mesosphere – Temperature again falls in the Mesosphere, producing the coldest temperatures experienced on our planet. The Mesosphere extends up to approx 80km.
Thermosphere – The concept of temperature starts to have less meaning by the Thermosphere where the mean free path of molecules starts to be measured in Metres and then Kilometres.
Exosphere – Above the Thermosphere is the Exosphere. We're now well inside what we describe as outer space. The Thermosphere extends out most of the way to the Moon. Particles in the Exosphere can travel hundreds of miles before colliding with another particle. It no longer behaves like a gas.
Under the Sea
 |
What if we go swimming? If we dive under water, pressure increases even further. Not only do we have the weight of the air, but we also have the weight of the water above us. However, this time the calculation is really easy. Remember, water is a liquid and is (practically) incompressible. The incremental pressure because of the water, therefore, is just the weight of the column of water above. The differential equation is similar to before, but this time the density is constant. 
Pressure increases linearly with depth. |
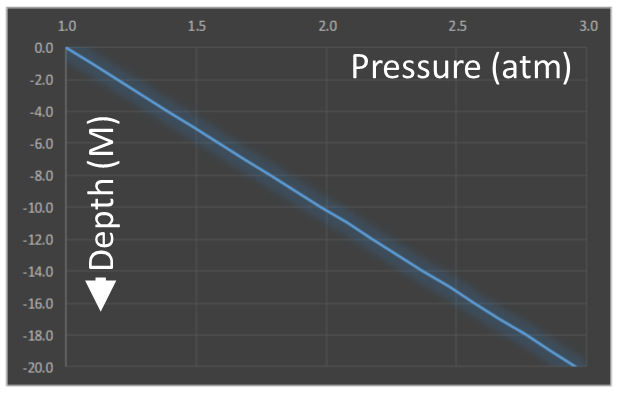
Pressure starts at sea level at one atmosphere (the weight of the air above) and increases with depth. Water is considerably more dense than air, so the pressure increases rapidly.
Consequences of pressure changes
 |
The changing of air pressure with altitude has many consequences. As mentioned earlier, it’s the reason planes fly at high altitudes in an attempt to minimize drag. The lower pressure at altitude in mountain regions lowers the boiling point of water. Climbers find it takes longer to cook food (and tea made at higher altitude, supposedly, does not taste as nice as that made lower down as the lower temperature of the water does not extract as many of the locked in flavours of the tea). |
|
Your car, when driving over a high mountain pass, may struggle a little more as the engine produces less power (the lower pressure air contains less oxygen per volume, so each time the engine breathes in a cylinders-worth of air, there is less to oxygen to burn the fuel, and a smaller bang is made). Interestingly, the opposite happens in forced induction engines (turbo-charged and supercharged engines). On these engines, the charger compresses the intake air to a higher pressure resulting in more oxygen per cylinder load, and thus, more to burn. This bigger bang gives more power. Forced induction engines suffer less from power-loss at altitude as the engine management system allows the charger to boost the intake air to compensate for the lower ambient pressure. |
 |
 |
The air outside an aircraft, when it is cruising at altitude, is at too low a pressure for our lungs to extract sufficient oxygen from (at 43,000ft, the air pressure is just one fifth of sea-level pressure), if you were exposed to this low a pressure, you would pass out in a very short period of time. For this reason the internal cabin is pressurized. Pressurizing raises the internal cabin pressure to a level that is comfortable to breathe in, but not all the way to full atmospheric pressure (this reduces the stress on the aircraft hull which has to safely support the difference in pressure between the inside and outside, like a giant sausage). Modern aircraft are pressurised to produce an internal pressure equivalent to approx 2km altitude. |
|
Over time, our bodies react and adapt to changes in pressure. People who move to locations at higher altitudes start to develop blood with a higher concentration of red blood cells. Red blood cells carry oxygen around our body from the lungs to where it is needed, and the higher concentration of red blood cells compensates for the lower partial pressure of oxygen in this rarefied air. Professional athletes capitalize on this by performing their training at higher altitudes. Training in these thin-air conditions makes their bodies produce more red blood cells than at sea-level. When they return to normal pressure, this richer blood allows more oxygen to be carried by their blood to their muscles, and makes them perform better. |
 |
 |
Mountain climbers do a similar thing to ‘acclimatize’ their bodies to the thinner air. Rather than attempting a dash to the top of a tall peak, they spend time at intermediate altitudes to ‘thicken’ their red blood count to allow more oxygen to be carried. |
If you liked this article, you might also like this one about how big space is or why water pipes burst.
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.


