Radiocarbon Dating
|
Carbon dating, more specifically Carbon-14 dating (also sometimes called radiocarbon dating), is a technique used to determine the approximate age of old objects. It has some limitations; for instance, it can only be used on organic material, but it is such an important tool that the developer of the method, Willard Libby, was awarded the Nobel Prize for his work in 1960. His technique revolutionized the sciences of archaeology and paleontology. |
 |
 |
Radiocarbon dating was one of the most significant discoveries in 20th century science. The basic principle in radiocarbon dating is to measure the ratio of quanitity of the isotopes 14C to 12C that is present in a sample. We'll see below how this is important: |
Isotopes
There are three naturally occurring isotopes of Carbon. These are 12C, 13C, and 14C. All of these have the required 6 protons, but differ in their number of neutrons.
 |
|
(What does trace mean in this context? The ratio of 14C to 12C is approximately 1.3 × 10-12)
Decay
As note above, 14C molecules are unstable and decay.
If that were the end of the story, we’d expect all the 14C to eventually decay away from the Earth, but this is not the case because fresh atoms are constantly being created.

There is a constant production of fresh 14C in the stratosphere from the bombardment of cosmic rays. These rays create neutrons, which, in turn, smash into atoms of 14N, creating 14C (with the release of a proton). These Carbon atoms combine with oxygen to form carbon dioxide, and the carbon dioxide becomes part of the circle of life.
n + 14
7N
→ 14
6C
+ p
This constant production and decay explains the (fairly constant) 14C/12C ratio quoted above of approximately 1.3 × 10-12.
 |
As long as an entity is breathing/photosynthesizing it is constantly part of the carbon cycle and this dynamic equilibrium. As a living entity continues to refreshes its carbon, it is constantly getting a fresh dose of 14C. The percentage of this isotope inside the living item remains the same, and in the same ratio as the carbon in the atmosphere. |
Once the entity dies and stops exchanging carbon, it has no way to replenish its 14C. The 14C inside the organism decays away. This is the basic principle of carbon dating. By measuring the amount of 14C left in the specimen we can estimate how long it was since the organism stopped living.
14
6C
→ 14
7N
+
e−
+
ν
e
Once an entity dies and stops exchanging carbon, it has no way to replenish its 14C.
Half-Life
|
Radioactive decay is not influenced by temperature or pressure (this again, is a tremendous advantage to radiocarbon dating). The standard way to measure the decay rate is with the Half-Life of the isotope. This is a measure of how long it takes for half of the molecules present to decay away (or more strictly the time required for exactly half of the entities to decay on average; in other words, the probability of a radioactive atom decaying within its half-life is 50%). A simple way of thinking about this is to imagine a bag of coins. At every half-life, flip all the coins, and discard any that land heads. |
As the half life of carbon is approximately 5,730 years, then an object that has one eigth of the concentration of 14C will be approximately three half lives old (3 × 5,730) ≈ 17,190.
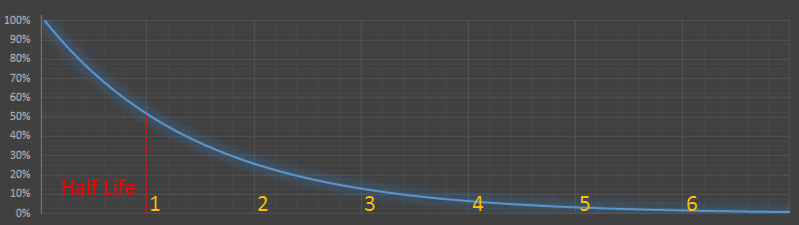
14C decays, with a half life of approximately 5,730 years, through the emission of an electron at 0.016 MeV (β decay) and an electron antineutrino. We now have all the pieces we need to see how radiocarbon dating works.
We know the ratio of 14C to 12C was fixed when the entity was living, and by measuring the ratio at the present time, we can find out how much of the 14C has decayed and, therefore, approximately how long has elapsed since the thing stopped breathing.
Detecting
The older something is, the less 14C remains in it.
 |
The early applications of the carbon dating technique measured the β particles emmited when the carbon decayed (the base rate is initially approximately 15 decays a minute per gram of Carbon). A more modern approach is to use a mass spectrometer to measure molecular weights and thus all the 14C is counted, not just the atoms that happen to decay. Not only does this give more accuracy, and allows dating of objects many more half-lives old (when the quantity of 14C is very small), it can also be used on much smaller samples of material. |
Calibration Curves
All of the above relies on the assumption that the level of 14C that was present in the atmosphere remained fairly constant over time. Analysis of samples taken from old trees (where the rings can be used to measure age) allows calibration (correction) curves to be generated that more precisely describe the ratios present at those times. (For more information on this, See here).
|
Today, we burn a lot of fossil fuel (coal, oil, and natural gas), and the carbon in these fuels comes from organic material buried underground a long, long time ago. The 14C present in these fuels is so low that their release into the atmosphere as CO2 dilutes the ratio of 14C to 12C. For this reason, without a calibration applied, modern objects would appear older than they really are. This effect is called the Suess effect, after Hans Suess, the first person to report it. |
 |
 |
A much larger effect comes from above-ground nuclear testing! These tests released large numbers of neutrons and created additional 14C. From about 1950 until 1963, when atmospheric nuclear testing was banned, it is estimated that several tonnes of 14C were created, doubling the levels of 14C in the atmosphere. |
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.


