Roulette Wheel
 |
This article is about roulette wheels, but first let's take a step back. One of my earlier blog postings was about dart boards. It asked the question: Where is the best place to aim on a dart board?(With the aim of getting the highest expected score with a single throw). This is not a trivial question because a dart board is cleverly designed. |
|
On a dart board, high scoring regions are located adjacent to low scoring regions. If you manage to hit a high scoring segment, great, but if you miss, you are penalized heavily. Other regions have lots of medium scoring regions as close neighbours. Maybe it is better to aim for one of these middling areas? You're not going to hit big scores, but you are not going to get low scores either. Do these things cancel out? The truth is (like so many things), it depends. |
 |
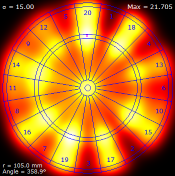 |
It depends on how skilful you are. If you are a great darts player, and can throw consistently then, yes, by all means aim for the high scoring regions; You'll hit these most of the time, and maximize your expected score. At the other end of the scale, if you are a really bad player, you should just aim for the bullseye at the center of the board. For you, getting any score from your dart is a win! Just hitting the board is an achievement! For players with skills in the middle, depending on how good (accurate) you are, your aiming point is going to change. If you are interested in learning more, I encourage you to read my earlier article. |
Roulette Wheel
We can see that there's logic to the arrangement of scores around a dart board. Because of control, an informed player can make the choice to aim for a high maximising potential scoring region (which has high variance), or make a more reliable, and less risky, shot to a mediocre region.
Why then, are the numbers in a roulette wheel arranged in a pseudo-random way? It's not as if a roulette player has any input as to where the balls lands. Why not place all the numbers in numeric order and be done with it?
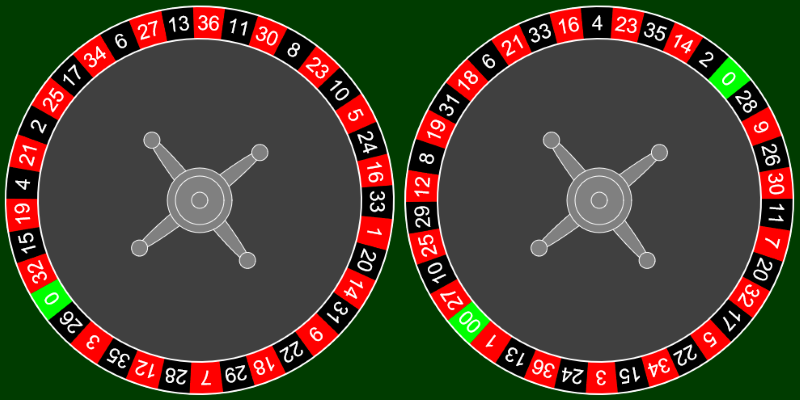
If we look at an official roulette wheel, the numbers are not in order:
 Image: bejadin.info
Image: bejadin.info
Why not just label them ordinally? Before we attempt to answer this, first let's take a look at how they happen to be arranged.
American and European
The name 'roulette' comes from the French, and the name means 'small wheel'. There is some indication that the invetor of the wheel was none other than the mathematician Blaise Pascal.
“You cannot beat a roulette table unless you steal money from it.”
There are two major styles of roulette wheel in use: European and American.
A European wheel has 37 pockets into which the ball can land. These are numbered 1-36, plus one numbered zero. The non-zero numbers are half red, and half black. Here is their ordering:
0 32 15 19 4 21 2 25 17 34 6 27 13 36 11 30 8 23 10 5 24 16 33 1 20 14 31 9 22 18 29 7 28 12 35 3 26
An American wheel has 38 pockets, the same numbering as the above, but also has a 'double zero' pocket (more on this later). Here is the ordering on an American wheel. (Notice that it's not just the addition of the '00' pocket; all the numbers are in different positions).
0 28 9 26 30 11 7 20 32 17 5 22 34 15 3 24 36 13 1 00 27 10 25 29 12 8 19 31 18 6 21 33 16 4 23 35 14 2
Here is what the two wheel variants look like. The European, with the single zero, is shown on the left. The American, with the a double zero, on the right.
There are some interesting things about the distribution:
|
 |
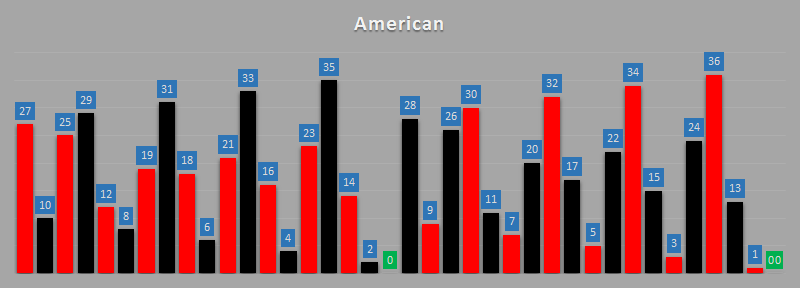
Here are the distributions in graph form. First the European:

Now the American:
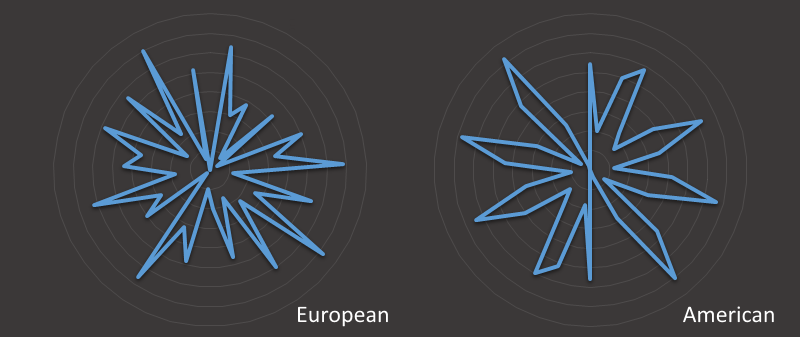
This is how these data look as radar plots. In the diagrams below, the radius shows the value of the pocket at that location. The radar plot of the European wheel (on the left) looks pretty random (but spikey, with every other point in or out). The plot of the American wheel looks a little more structured.
Random or design?
If a roulette wheel is well manufactured and operated, it should be a fairly efficient random number generator (in fact, if we are to believe history, Blaise Pascal invented the roulette wheel as a mechanism for generating random numbers).
With no bias or favouritism for any pocket, the ordering of pockets should not be important. We come to the conclusion that the ordering is therefore psychological in nature.
It's my speculation that the numbering is for both superstitious and clever marketing reasons.
By making the numbering appear random (no obvious pattern), it reinforces that this is a game of chance. Somehow if all the numbers were ordinally arranged this would seem less obvious.
Care is taken to 'balance' out the wheel so that similar numbers are not adjacent or close (as if this is important!) to somehow reinforce that the wheel is fair and 'even'. I'm sure this is important to those that believe in some concept of 'conservation of luck' (The Gambler's Fallacy).
Having no discernable pattern implies that it is not obvious which numbers are adjacent to each other, again reinforcing the 'randomness'. (Interestingly though: I'm not a roulette player, but I have been told by regular players that, after a while, you do quickly learn the ordering of the numbers).
Distribution
We saw, earlier, the variance of the numbers around the wheels. The European version shows no obvious patterns. The American version shows a litle more structure and, as we have seen from the specification of the wheel layout, opposite numbers vary by only one 'unit'. (As if two numbers being numerically adjacent to each other has any skin in the game of how they are randomly selected!?!)

Taking this a stage further, we can plot out the 'rotational moving average' (I think just made that term up) of the wheels. The top row in the plots below shows the three-period average. What I have done is take the value of the pocket, and the value of the pockets on either side, and averaged them. This 'smooths' them out.
I've also generated the five-period average. Here I taken the two values clockwise, and the two values counter-clockwise, and the value of the pocket itself and average out all five of these.
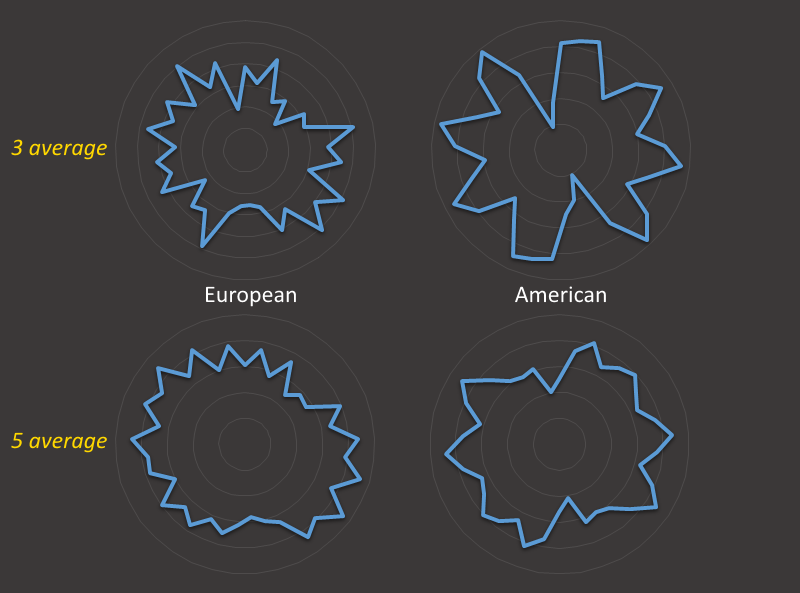
People of a superstitious nature will be pleased to learn that the radar plots of these values are nicely 'round' and 'smooth' implying the wheels are 'balanced' and 'fair'. Poppycock :)
“I used to be superstitious, then I heard it was unlucky, so I stopped!”
Update: European and American
In researching this article, I discovered another difference between American and European roulette wheels. This is a subtle difference, and one that I did not find well documented, but photo research seems to uphold.
 Images: k-bot, mattbuck007
Images: k-bot, mattbuck007
On a European wheel, the numbers face the center of the wheel. On an American wheel, they face outside. This is one of those things that, once you've seen, you can never un-see, but until pointed out to you, you probably never noticed!
Was Einstein Wrong?
 |
There are no betting systems that will allow you to consistently win money from roulette. Albert Einstein once said that “You cannot beat a roulette table unless you steal money from it.” When I was teenager, one of the books I, fondly, remember reading was called The Eudaemonic Pie. A non-fiction book about the exploits of a group of talented students from the University of California, Santa Cruz. Designing what was (probably), the World's first wearable computers (which they installed into hollow shoe heels) so that they could exploit biases in incorrectly balanced and configured wheels. After programming and calibrating their computers to the percularities of a target wheel, using a modelling algorithm based on the physics, they claim that they were able to predict which 'octet' of the wheel the ball was more likely to land it. This could be exploited, and bets made to overcome the house odds and make a positive expected outcome. Originally published in 1985, the book is still available today from Amazon. The book describes the research, design, training and use of this device. I'll not spoil the plot if you are interested in this (factual) piece of history. |
House odds and double zero
|
So, why does an American wheel have a double zero pocket in addition to a single zero? The simple answer is house odds (casino profit). There are multiple ways to bet on a roulette wheel: Betting on a single number, betting if the number will be odd or even, betting if it will be red or black, if it will be high or low. There are more complicated bets based on ranges of numbers. For a complete list of the bets, Google is your friend: Roulette Bets. |
 |
Below is a representation of what a (European) betting table looks like:
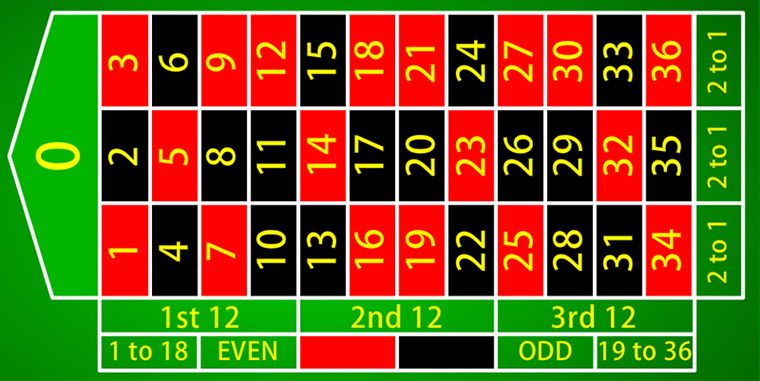
A casino pays out even-money on bets based on red/black outcome, or odd/even, or high/low. If you bet $1, and you are correct, you get your original stake back, plus an additional dollar. If you lose, you lose your bet.
 |
If there were only the numbers 1-36 on the wheel, it would be a 'coin-flip', with a 50:50 chance for each of these bets. Good (or at least neutral) for the player, but bad for the casino (there is no take, or profit). This is where the zero comes in. Zero is neither odd nor even (that's a mathematical debate for another day, but for casino, it's a definite no!). Zero is neither red nor black. It's neither high nor low. The presence of the zero skews the probability. One time in thirty-seven (on average) it will get landed on, and so the even-payout on these coin flip bets now gives an advantage to the casino. It's a similar story if you bet on a single number. The casino pays out 35:1 if you successfully predict a single number. Not bad, if it were not for the presence of the zero. Below is a table of the common roulette bets, their corresponding payouts, and the probability of achieving this bet (for a European wheel). |
The difference between the payouts made and the probability of achieving these is the the casino profit (called the house odds). For a European roulette wheel, because of the presence of the zero, the house odds are 2.70%
(If you bet on red, you would win 18/37 times, and lose 19/37 times. The difference between these, as it is an even money bet, is the expected outcome and is 18/37 – 19/37 = –1/37 ≈ –2.70% and the house odds.)
| European Table Bets | Payout | Probability |
|---|---|---|
| Odd | 1:1 | 48.65% |
| Even | 1:1 | 48.65% |
| Black | 1:1 | 48.65% |
| Red | 1:1 | 48.65% |
| 1-18 | 1:1 | 48.65% |
| 19-36 | 1:1 | 48.65% |
| 1-12 | 2:1 | 32.43% |
| 13-24 | 2:1 | 32.43% |
| 25-36 | 2:1 | 32.43% |
| Single Number | 35:1 | 2.70% |
| Combination of two numbers | 17:1 | 5.41% |
| Combination of three numbers | 11:1 | 8.11% |
| Combination of four numbers | 8:1 | 10.81% |
| Combination of six numbers | 5:1 | 16.22% |
Below are the corresponding American table odds. You can see the payouts are still the same, but now there is an additional pocket on the wheel, the double zero. This modifies all the probabilities (all in the favor of the casino). The addition of the double zero increases the house odds to 5.26%
| American Table Bets | Payout | Probability |
|---|---|---|
| Odd | 1:1 | 46.37% |
| Even | 1:1 | 46.37% |
| Black | 1:1 | 46.37% |
| Red | 1:1 | 46.37% |
| 1-18 | 1:1 | 46.37% |
| 19-36 | 1:1 | 46.37% |
| 1-12 | 2:1 | 31.58% |
| 13-24 | 2:1 | 31.58% |
| 25-36 | 2:1 | 31.58% |
| Single Number | 35:1 | 2.63% |
| Combination of two numbers | 17:1 | 5.26% |
| Combination of three numbers | 11:1 | 7.89% |
| Combination of four numbers | 8:1 | 10.53% |
| Combination of six numbers | 5:1 | 15.79% |
| Combination of 1-2-3-0-00 | 6:1 | 13.16% |
It's now pretty clear why casinos like wheels with a double zero!
There is no 'skill' involved in playing a game of roulette. After the bets are placed, the player has no influence in the outcome. The odds, as we have seen, are in the favour of the casino (in the long run). It's up to you if you decide the fun you get from playing (along with the potential of making money in the short term), outweighs the 'tax' of the house cut.
 Image: bejadin.info
Image: bejadin.info
Try it out
For a little fun, I wrote a little roulette simulator. You can toggle between the American and European wheels. Pressing the spin button gives the wheel a random spin.
To the right of the wheel, the last ten outcomes are displayed. Caveat: It's only a few lines of code, and is not supposed to be a proper roulette or full featured simulator; please don't email me about it!
(For some reason, performance on my iPad seems very poor and I'm getting pathetic frame rates. Performance on my desktop browsers, and lower spec Android devices seems fine. I'm using the Processing library for the graphics. I'll see if I can find out reasons why).
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.

