
	Advertisement

Spheres in Cylinders

Last week I wrote about the maximum (volume) cylinder it’s possible to fit inside a sphere.

A couple of people asked me about the inverse of this problem: What is the largest sized sphere you can fit inside a cylinder? It’s not quite the same problem however because, to describe a cylinder, we require two parameters: The radius and the height.

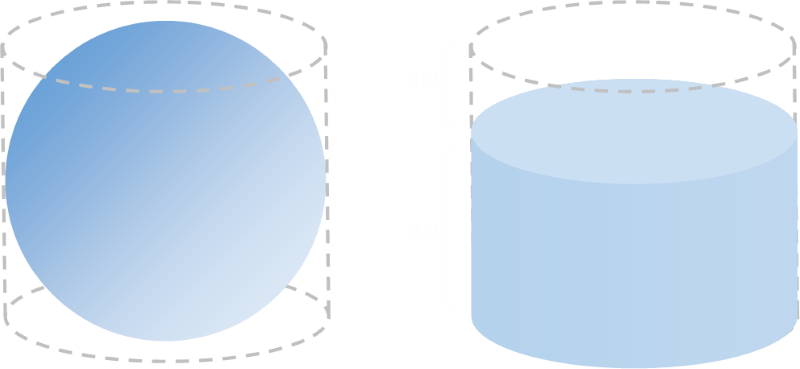
What we’re going to assume the sphere sits in a cylindrical tube, and the end caps of the cylinder just touch the sphere.

“What is the ratio of the volume of the sphere to the volume of the cylinder in the diagram to the left?”

The sphere has a radius of: r
The cylinder has a radius of: r
The cylinder has a height of: 2r

Eureka!

The solution to this problem was first discovered by Archimedes, the famous Greek mathematician. He was so proud of his solution that he requested of his friends and family that a graphic of a sphere inscribed in a cylinder be carved on his tomb.

Archimedes based his proof using geometry. Today, we are blessed with the understanding Calculus, and formulas for the volumes of basic shapes are taught to all in High School.

What pleased Archimedes so much about the solution is that the ratio of the volume of the sphere to the cylinder is the same as the ratio of the surface area of the sphere to the surface area of the cylinder!

Math

The formulas for the volume of a sphere and the volume of a cylinder are well known. The height of the cylinder is twice that of the radius of the sphere.

As we can seem the ratio is 2/3.

The surface area of a sphere is also a well-known to anyone who has spent teenage years in math class.

The surface area of the cylinder can be calculated by adding the area of the two circular end caps to that of the rectangle that wraps around (like the label on a soup can). Again the height is twice the radius.

Noli turbare circulos meos

As you can see, the ratio of the volumes is the same as the ratio of the surface areas, and this constant is 2/3.

I'm convinced that there has to be some fantastically useful consequence of this result, but I can't think of one just at the moment.

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.