ROT13 and Caesar Ciphers
THE QUICK BROWN FOX SAID I LOVE LUCY
GUR DHVPX OEBJA SBK FNVQ V YBIR YHPL
ROT13 (short for “rotate 13 places”), is an obfuscation technique familiar to nerds, geeks, and computer programmers. It’s commonly used in online forums as a means of hiding or obscuring spoilers, punchlines, hints, and (sometimes) offensive content.

I’m hesitant to call it encryption because it’s so weak. What it is is a simple substitution cipher (in fact, it's worse than that because, as described below, it's a Caesar Cipher in which the offset for each character is the same and fixed!)
To execute ROT13 you take a letter and shift it along 13 places (and if you go over the end past ‘Z’, you wrap around again to ‘A’). It jumbles the letters up sufficiently such that, at first glance, you can’t read the message, and that, these days, is its only real purpose. If you attempt to use it to store/encrypt passwords or sensitive information you deserve to have your programming license revoked!
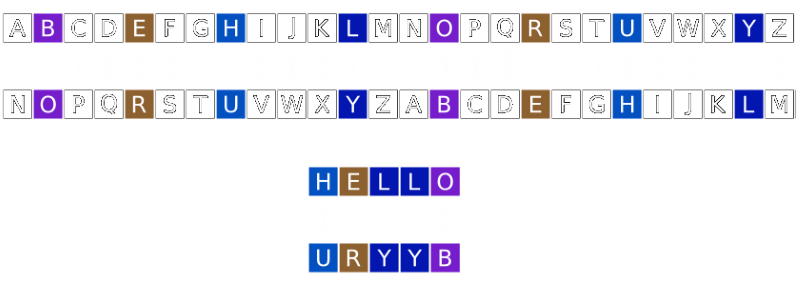
It’s such a popular technique that some text editors and news readers have ROT13 functionality built in!
As an example of how this works the word “HELLO” gets converted by ROT13 into “URYYB”
Traditionally, ROT13 is only applied to the letters ‘A-Z’ and ‘a-z’ so that case, numbers, and other punctuation are preserved.
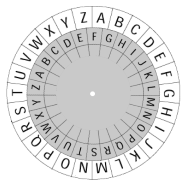 |
When you were a kid (perhaps you still are one), you might have had fun using some kind of Spy code/de-code wheel. On these devices, the letters ‘A-Z’ are written on concentric disks which can rotated to offset the alphabet. Two ‘secret agents’ agree on the offset beforehand then, to encode a message, the desired letter is selected on the inner wheel, and the coded letter read on the outside wheel. The process is then inverted by the decoder to read the message. To use a decoding wheel for ROT13, simply rotate the wheel 13 places. |
Why ROT13?
Because the English alphabet has 26 characters, ROT13 has the interesting property that it is self-inverting. Performed twice on a piece of text reverts the text back to the original. It is for this reason that ROT13 became so popular.
ROT13('HELLO') = 'URYYB'
ROT13('URYYB') = 'HELLO'
ROT13(ROT13('HELLO')) = 'HELLO'
If you are familiar with Boolean logic, this is a property similar to the XOR operator. If performed twice with the same argument, XOR returns the input to the same value.
To encode/de-code in ROT13 you only need one command, and you can't get it the wrong way round either!
ROT5
Similar to ROT13, which applies to letters, it’s possible to obfuscate numbers with a similar self-inverting rotation of five places.
43,252,003,274,489,856,000 ↔ 98,707,558,729,934,301,555
There is a hybrid system which encodes text using ROT13, numbers using ROT5, and leaves all other characters unaffected.
ROT5 is subtle, numbers just look like numbers should!
ROT47
Another (less-popular) variant is ROT47 which shifts the 94 characters from ASCII 33 (which is the “!” directly after the space) to ASCII 126 “~”. This obfuscates letters, numbers, and punctuation characters but still keeps the output in 7-bit ‘safe’ printable ASCII.
Call the number (425)-555-1212, and ask for "Princess"
r2== E96 ?F>36C WcadX\ddd\`a`a[ 2?5 2D< 7@C Q!C:?46DDQ
ROT47 is far from subtle; it's pretty clear that the message above has been encoded.
Caesar Ciphers
THE QUICK BROWN FOX SAID I LOVE LUCY
GUR DHVPX OEBJA SBK FNVQ V YBIR YHPL
Using ROT13 as anything more than obfuscation technique has more security holes than a piece of Swiss Cheese. A simple rotation cipher is given the name Caesar Cipher, after Julius Ceasar, as it is documented he used this technique to 'protect' messages to his troops (he is documented as using ROT3, whilst his nephew used ROT1).
Once you know the technique used, it's fairly trivial (even using brute force if you don't know the offset), to enumerate all possible versions to reveal the source message!
| ROTn | Cipher |
|---|---|
| 0 | THEQUICKBROWNFOXSAIDILOVELUCY |
| +1 | UIFRVJDLCSPXOGPYTBJEJMPWFMVDZ |
| +2 | VJGSWKEMDTQYPHQZUCKFKNQXGNWEA |
| +3 | WKHTXLFNEURZQIRAVDLGLORYHOXFB |
| +4 | XLIUYMGOFVSARJSBWEMHMPSZIPYGC |
| +5 | YMJVZNHPGWTBSKTCXFNINQTAJQZHD |
| +6 | ZNKWAOIQHXUCTLUDYGOJORUBKRAIE |
| +7 | AOLXBPJRIYVDUMVEZHPKPSVCLSBJF |
| +8 | BPMYCQKSJZWEVNWFAIQLQTWDMTCKG |
| +9 | CQNZDRLTKAXFWOXGBJRMRUXENUDLH |
| +10 | DROAESMULBYGXPYHCKSNSVYFOVEMI |
| +11 | ESPBFTNVMCZHYQZIDLTOTWZGPWFNJ |
| +12 | FTQCGUOWNDAIZRAJEMUPUXAHQXGOK |
| +13 | GURDHVPXOEBJASBKFNVQVYBIRYHPL |
| … | … |
There are only 25 rotations to try by brute force!
Substitution Ciphers
Closely related to Caesar Ciphers are Substitution Ciphers. These still map 1:1 between each character in the source text and cipher text, but adjacent characters in the source do not have to map to adjacent ones in the destination.

If spaces are preserved in the encoding, it's easy to see where the word breaks are, and thus you can guess at what you think are the more popular words. As each character is always converted over to the same replacement character, common words (and commonly occurring groupings and patterns of letters) start to jump out of the page very quickly (especially if the message is quite long). Removing the white space between words adds a trivial level of complexity.

Substitution ciphers don't have to just use other letters. Symbols can be used. Two of the most well known examples of this are "The Dancing Men", from the famous Sherlock Holmes story, and the "PigPen Cipher" which uses fragments of grids and dots to represent the alphabet.

Solving Substitution Ciphers
Even with, or without, spaces removed, substitution ciphers are fairly trivial to guess. There's a 1:1 mapping between each character so, once you know one conversion, you know all other occurrences of that same character (and you also know that this letter can't be used again).
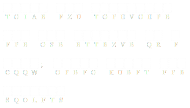 |
The solution space is so small that the solving of these is a hobby (like solving Crossword puzzles, word searches, or Sudoku). These puzzles are called Cryptograms. An example is shown on the left for the quote: "Style and structure are the essence of a book; great ideas are hogwash." - Vladimir Nabokov |
The strategy for solving cryptograms is a combination of brute force, heuristics, and letter/word frequency.
Not all letters in the English language are used equally. Some, like the letters 'E', 'T' and 'A' are used very frequently. Unless the message we are trying to decode is very obscure, we'd expect the distribution of symbols in the solution to follow a similar profile. This alone could give a first pass for decoding a message; we simply apply the frequency of letters used in the secret message to the frequency we expect for each letter.
From Wikipedia, here is the ordering of letters in English language (taken from a corpus of many hundreds and thousands of documents):
ETAOINSHRDLUCMFWYPVBGKQJXZ
(You might also like an article I wrote few years ago about the game of Hangman and letter distribution).
If our secret message is a representative sample of the entire English language, we'd expect the symbol representing "E" to be the most frequently occurring in our message, followed by "T", then "A" …
This is far from perfect; the chances are our message is short, and so the letters might not follow this distribution perfectly (or even have enough granularity, or even use all the letters of the alphabet). We can narrow down solutions using brute-force and Chi-squared tests of letters frequency based on expected, but there is so much more we can do very easily.
If white spaces are present, we can apply knowledge of the words in the English language. We know that there are only a limited number of two, three and four letter words, and these words are common. Did you know that one third of all printed English materials are made up of the top 25 occurring words? (The most popular 100 words make up approximately half of all printed English!)
the, of, and, a, to, in, is, you, that, it, he, was, for, on, are, as, with, his, they, I, at, be, this, have, from
Guessing which word could be which and corroborating this with what these symbols/letters would be like in the other words could be a great help.
If there is no white space to give word breaks, we can still apply statistical techniques. Certain combinations of letters often occur together. It's very common to have "TH" next to each other and "ER" and "RE". Certain letters often occur in double form, like "OO", "EE" and "LL". Conversely, have you ever seen a word containing "JJ"*?
We're taught an early age that it's very common for "Q" to be followed by "U". Although "Q" is not a popular letter, if we do identify one, there's a very good chance the letter after it is a "U". There are similar rules with other letters.
Most (not all), words contain at least one vowel (AEIOU), and if you include "Y" as a vowel you practically include all words. The more letters you lock in, the easier it gets to solve the rest (both because you have partial words to complete, and the unused letter pool is smaller).
*I can only think of: HAJJ, HAJJES, HAJJI, HAJJIS
Let's take a look
I was curious about letter distribution, so I downloaded a dozen books in plain text from Project Gutenberg. This site has 50,000 free books available!
If you are interested, the books I selected (randomly from the fiction collection) were:
|
 |
Obviously, the more books you sample the more refined your distribution will become for generic solving. Alternatively, if you have some idea of the context of your secret message, you might elect to sample a more specific set of books to more accurately represent the sample you have.
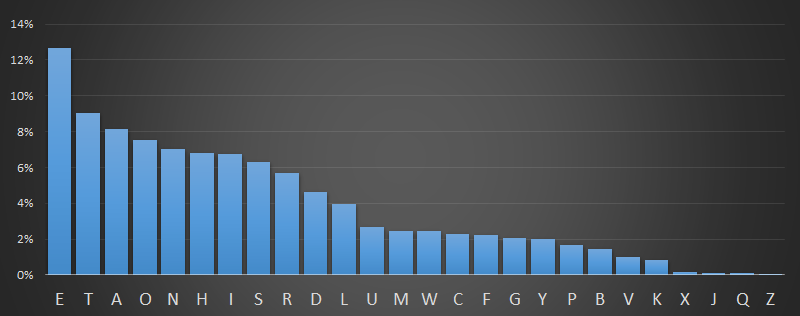
Single Letter Frequency
Based on the books above, here is the single letter frequency distribution. The percentages show the percentage over the total of all the letters in these books (Approximately 9 million letters).
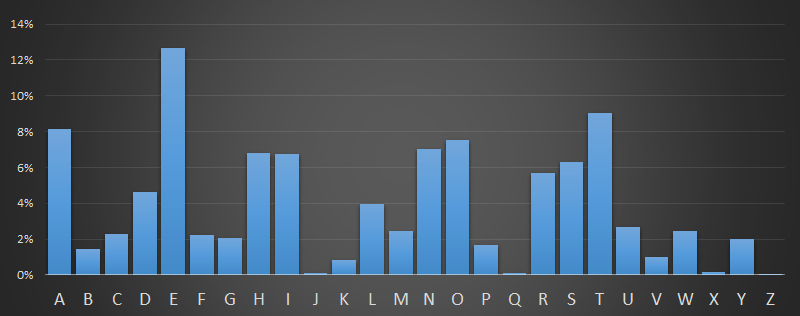
Here is the same data plotted in sorted order. The ordering is slightly different to the answer given by Wikipedia, but that's because we're using different samples.
Bigrams
Next I looked at the frequency of all bigrams (also called couplets of letters, adjacent pairs, and sometimes called digrams).
To generate this list I ignored any white space and punctuation characters. So, for example, in addition to containing all the letters that occur next to each other inside of words, this list also contains entries for the words that end with the first character that occur adjacent to words that starts with the second. This will help if your secret message does not contain white space that allows you to determine where the line breaks are.
Here are the most frequently occurring top 50 adjacent pairs of letters:
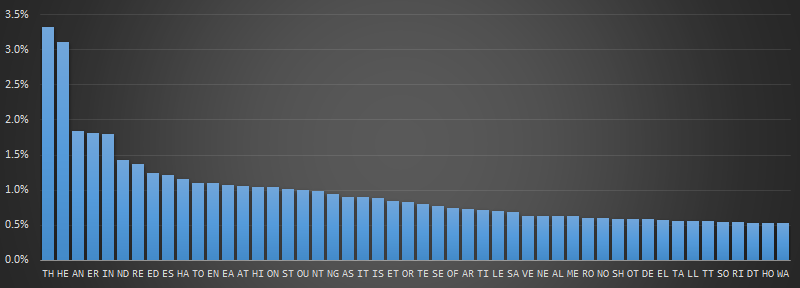
Interestingly, even though there are 26 characters, the total number of bigrams in my sample is not 26 × 26 (=676). Instead there are 643 distinct items. Not every possible pairing of characters occur (for instance the pairing "QZ" or "ZX" never occurred in the books I sampled).
As expected the frequency of "TH" and "HE" dominate. These bigrams are popular in many words as well as the most common words.
Note - This is a great data to use if you have no information about either of the characters. However, if you know, for instance, one of the characters in the pair you can use this information to find conditional probability. For instance, if you know a pair is "Q?", then the there is 99.9% chance that the missing unknown character is a "U".
Here are the top 200 bigrams in tabular order:
|
|
|
|
Trigrams
The next logical expansion is to look at trigrams (sequences of three letters).
There are 9,671 distinct trigrams in my sample (cf. 26 × 26 × 26 = 17,576 possible).
Again seeing "THE" at the top is no surprise, neither is "AND". These are both popular words in their own right, and sub-strings of other words. "ING" comes next as the suffix for many verbs, followed by many other triplets you can find inside common words.
Here are the top 200 trigrams in tabular form:
|
|
|
|
Quadgrams (or is is Tetragrams?)
After three, comes four. I'm not sure if it's correct to call them quadgrams or tetragrams (Latin or Greek?), so instead we'll just call them n-grams or 4-grams.
There were 87,526 4-grams in my book samples (cf. 26 × 26 × 26 × 26 = 456,976 possible; less than 20% of the theoretical possible combinations).
Here are the top 200:
|
|
|
|
Things get a little more complicated as we move to four characters. Top of the list is "THER", some of which could be from the word "THE", followed by a word starting with "R", but a a most of the frequency of "THER" comes as it being part of words like "THERE" and "OTHER" (and all those other words that have this sub-string contained in them).
Looking through the list it is easy to see words that are distinct popular four character words in their own right as well the sub-strings.
5-grams
There were 434,396 5-grams (cf. 26 × 26 × 26 × 26 × 26 = 11,881,376 possible; less than 4% of the theoretical possible combinations).
Here are the top 200:
|
|
|
|
Things get even more interesting here. "OFTHE", "ANDTH", "TOTHE" and "INTHE" at the top are all obvious concatenations of two words. "THERE" comes next.
As the n-grams become longer it's possible to start seeing more distinct (and specific) words. As I was testing the code out with smaller books, after pausing and viewing the intermediate results, it was possible to identify sub-strings of titles characters and specific nouns in the books.
This shows us that, unless we're aiming to decode a message with a defined dictionary of possible words, going too deep into n-gram analysis will start to hurt us. Up to about 4-grams, we're mapping the characteristics of the English language. Above 4-grams, it's looking like we are starting to map more to words than distributions of groupings of letters.
6-grams
The error of going too deep into n-gram is confirmed looking at this list. It doesn't take too long see specific words that obviously belong to one specific book.
There were 1,239,584 6-grams (cf. 26 × 26 × 26 × 26 × 26 × 26 = 308,915,776 possible; less than 0.4% of the theoretical possible combinations).
Here are the top 200:
|
|
|
|
Final return to ROT13
As I was messing with ROT13, It wondered if it was possible to to apply ROT13 to a word and make an entirely different (valid) word. A few lines of SQL late revealed there are quite a few possible. The longest found in my dictionary file was NOWHERE ↔ ABJURER
NA↔AN NAAN↔ANNA NAG↔ANT NAN↔ANA NAVY↔ANIL NE↔AR NIB↔AVO NO↔AB NOB↔ABO NOON↔ABBA NOWHERE↔ABJURER NU↔AH NUN↔AHA OHO↔BUB ON↔BA ONE↔BAR ONES↔BARF ONYX↔BALK OR↔BE ORA↔BEN ORRA↔BEEN ORT↔BEG OVA↔BIN PENNY↔CRAAL PENT↔CRAG PERRY↔CREEL PRY↔CEL PUNG↔CHAT PURS↔CHEF RAIL↔ENVY RAT↔ENG RE↔ER REAR↔ERNE REE↔ERR REEF↔ERRS REF↔ERS RET↔ERG ROOF↔EBBS SEL↔FRY SENT↔FRAG SERER↔FRERE SHA↔FUN SHE↔FUR SYNC↔FLAP TANG↔GNAT TERRA↔GREEN THY↔GUL TRY↔GEL TUNG↔GHAT UN↔HA UREA↔HERN VEX↔IRK WHA↔JUN WHEN↔JURA
Encryption Humour
 |
This web page is encrypted with ROT26. |
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.

