
	Advertisement

Congruent Rectangles in a Square Puzzle

Another geometry puzzle this week:

Imagine you have a unit square. From one edge you mark off a rectangle. If it is possible to place an identical (congruent) rectangle at an angle inside the complementary part of the square, what is the width of these rectangles?

(I believe the origin of this puzzle is a question from the American Math Competition).

Solving

At first glance it looks as though we might not have enough information to solve this problem, but let's take a look.

Let’s define the width of the rectangle to be x.

We know, already, that the height of the rectangle as one unit.

We have no other information about the geometry, but we know the rectangle on the bias touches each of the edges.

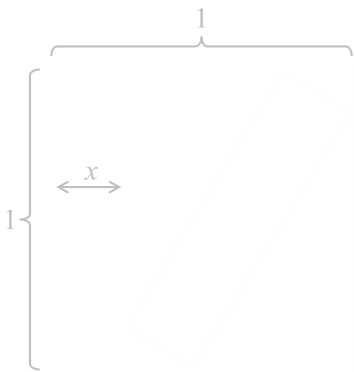Let's label what we know

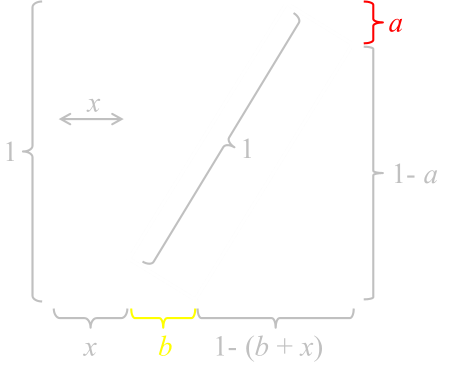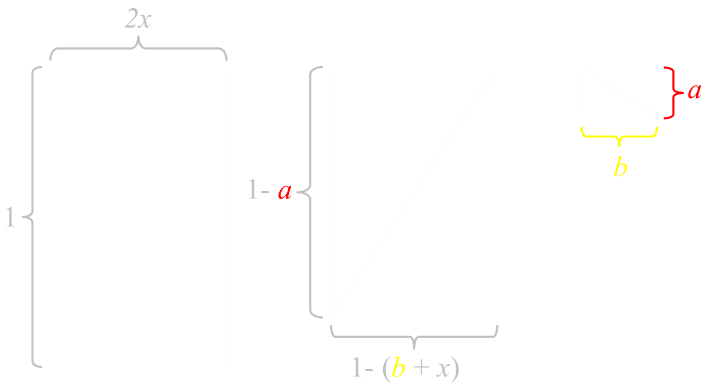
The first step to solving is label what we know.

We know the height and width of the square is one unit, and the rectangle on the left has width of x, so the complementary rectangle has a height of one unit and a width of (1-x) units.

The bias rectangle splits the region into two pairs of similar right-angle triangles.

We'll define one side of the 'smaller' triangle to be a, and one side to be b. (We know the hypotenuse of this triangle is x).

With some simple algebra we can calculate that sides of the 'larger' triangles are 1-(b+x) and (1-a) respectively, with a hypotenuse of one.

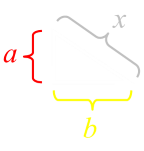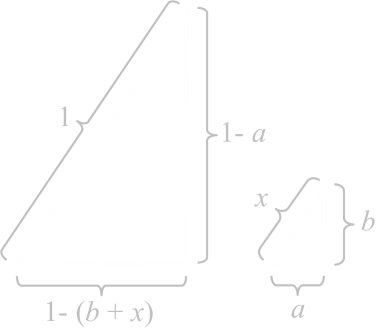As the triangles are similar, the ratio of their sides is the same. We can use this to derive a relationship between a and b.

The ratios of the adjacent sides to the hypotenuses are:

Conservation of Area

We know the square has a total area of one square unit. This area remains the same when it is carved up into pieces.

I'm going to solve this puzzle by equating the sum of the areas of each of the smaller pieces.

(I'm sure there are probably more elegant ways to solve this problem using trigonometry. If you find a particularly simple way, drop me an email!)

There are six pieces in total which can be grouped into pairs.

There are the two rectangles, and the two sets of triangles.

The pairs of triangles can be arranged to make two rectangles.

We can easily determine the dimensions of each of these three rectangles:

We know the total are of the square is one square unit, and we know this is the same as the sum of these three rectangles:

From the similar triangles, we know a=(1-b/x)

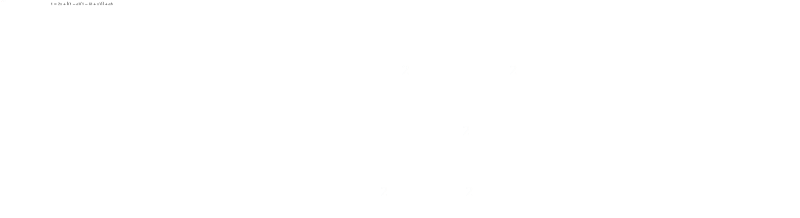
Applying the 'difference of two squares', and cancelling:

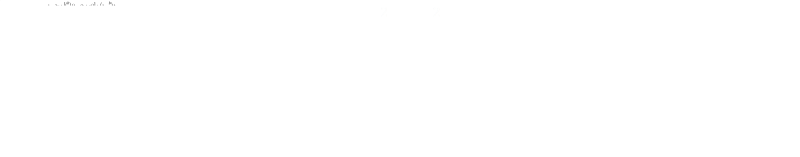
This gives our first result. It tells us that the corner of the bias rectangle touches the square, interestingly, exactly half way along.

We can substitute this result back into similar triangle result to also get an equation for a in terms of x:

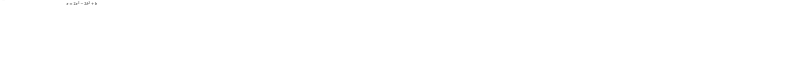
Returning to the smaller triangle, we can apply Pythagoras, and spoon into this values for a and b in terms of x:

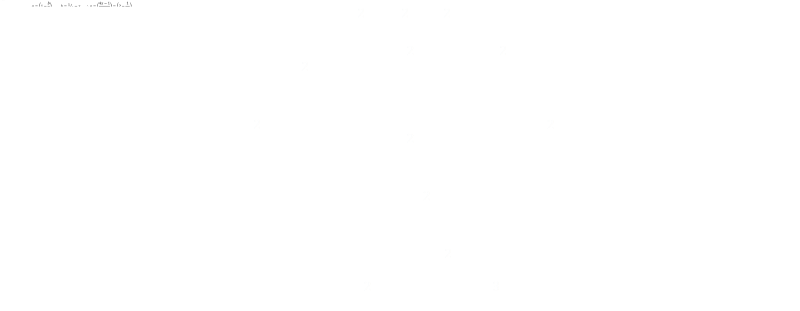
I have to admit, this got a little messier than I first expected, but we're almost home. All we need to do is factor this out and then we can find the roots).

This gives the following solutions:

The first root implies that a=0, so we can reject. Similarly the last root would give a value of x>1, leaving the middle root as the only valid solution.

Solution

(The other two roots are 'valid' solutions; meaning that they represent sets of polygons whose areas add up to a unit square, it's just that they don't meet the other criteria to be solutions based the other geometeric constraints.)

Update

For a different (trigonometric) way of solving this same puzzle, click here.

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.