
	Advertisement

Congruent Rectangles Puzzle v2

Last week, I wrote about a fun little geometry puzzle. Here it is again:

Imagine you have a unit square. From one edge you mark off a rectangle. If it is possible to place an identical (congruent) rectangle at an angle inside the complementary part of the square, what is the width of these rectangles?

The solution I published involved equating the areas of the different shapes. A few of you* wrote in suggesting alternative (simpler?) solutions involving some basic trigonometry. This posting is a hybrid of these.

*Special shout outs to: Stephen Li, Javier Romualdez, Scott Carr and George Xie.

You can see details of my solution last week here.

Trigonometric Solution

As before, we'll define the width of the rectangle to be x and we'll also define the angle the second rectangle makes with the horizontal to be θ. We can mark similar angles on the diagram.

We can create two equations for x in terms of θ by summing up the edges of the square (vertically and horizontally) and equating these to one (the width of the square).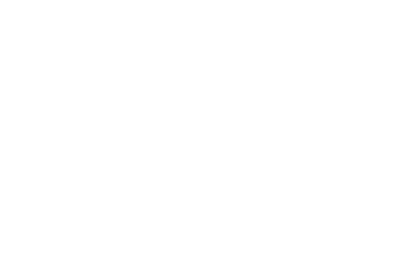

Equating these two equations and simplifying:

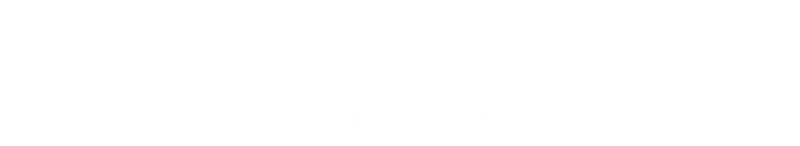
Using what was (probably) the second trig identity you ever learned (the first being sinθ/cosθ=tanθ)

We can can simplify and reduce down to this:

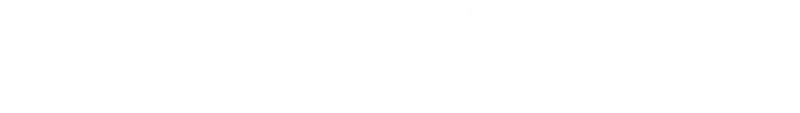
This important result tells us the shape of the triangle. Using Pythagoras we can determine the adjacent edge ratio and thus cosθ

Result

Inserting the values for cosθ and sinθ back into equation 1, we get the answer:

Thankfully, this is the same answer as the one we obtained by the (slightly more convoluted) method of conservation of area

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.