
	Advertisement

Five Circles Puzzle

Today’s article is about a puzzle I heard recently. This puzzle interested me enough to write some code to find the solution(s). This article is how I went about solving the puzzle. I don’t claim my solution is the best way to solve the problem. There may be better, more elegant, faster, or neater ways to find answers. This is just how I solved it.

Definition

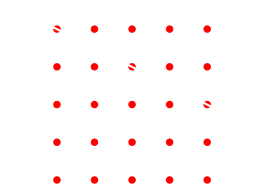
The puzzle is pretty easy to describe:

There is a square grid containing twenty-five points, all equally spaced and arranged in a 5 × 5 layout. Over this grid you can draw circles that pass through points (a couple of examples are shown on the left).

Here’s the question: Is it possible to use just five circles and make sure that at least one circle goes through every point on the grid?

I’ll cut to the chase. Yes, it is possible, and there are multiple solutions.

Solving

I elected to solve this problem by brute force. There’s a finite number of circles and arrangements of these circles, and we can work through all combinations of them to test to see if they meet the success criterion. There are some optimizations and pruning we can do as we go along to make the problem go a little faster than first appears.

What makes a circle?

Just like any three points can make a triangle, any three points on a flat plane can also be connected with a circle.

There is only one circle that fits through three points. (There are an infinite number of circles that pass through two points, and similarly for one point, but since we’re trying to find an optimal solution, we’re going to assume that all circles drawn pass through three (or more) points. In fact, as there are 25 points and five circles, some of the circles are going to have to pass through more than three points!)

Geometrically, finding the circle that fits through three points is equivalent to finding the circle that circumscribes the three vertices of the triangle these points make. A common way to do this is through the construction of perpendicular bisectors (Divide each side of the triangle in half, and draw from this point a perpendicular line. All three of these perpendicular bisectors will cross at a common point, and this point will be the center of the circle that passes through the vertices).

Another way to calculate the circle is with some algebra. The equation for a circle is pretty simple. All points on a circle are the same distance from the center of the circle. Using Pythagoras we can determine the relationship between the radius of the circle r, the center of the circle (OX, OY) and any point on the circle (x_p, y_p).

With three points on the circle we can create three simultaneous equations. With three equations and three unknowns (the x and y coordinates of the origin of the circle, and its radius r) we can solve.

A more structured way of describing these simultaneous equations is through the solving of determinants and matrices. The equations below can be solved to find the origin of the circle. Once we know the origin, the radius is easy to determine using Pythagoras and any of the points.

Any three points

We now have a way of determining the equation of a circle that passes through any three points.

The first stage of solving this puzzle is to write three nested loops to iterate through all combinations of three points on the grid. This will give us a collection of all the possible circles. There are 25 possible positions for the first point, 24 possible for the second point, and 23 for the third. (I'm electing to ignore the equivalence of reflections and rotations).

Problem

There’s a slight glitch in this approach.

It's possible for three chosen points to be co-linear. What does this mean? If all three points are in a straight line then, technically, they are still connected by a circle, but this circle has infinite radius. If we allowed this, then it would be a pretty trivial problem to solve (we could just draw five lines through five points each!)

I'm going to calculate solutions where each circle has finite radius.

We need a way to determine if points are co-linear.

If three points are co-linear then the gradient of the lines connecting them are the same:

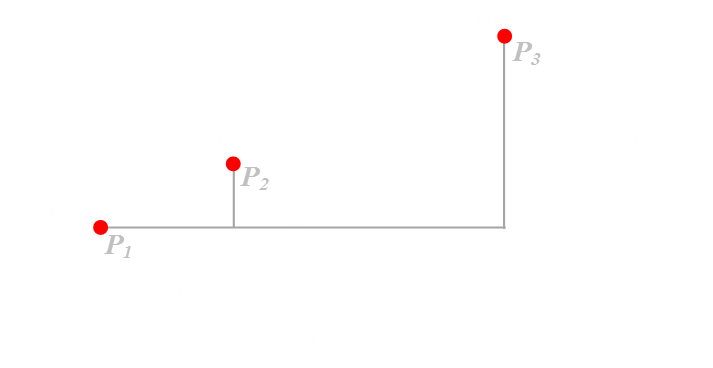
If the points are co-linear, the gradient of the line P1-P2 should be the same as the line P1-P3.

Testing that the above equation is zero should be a sufficient test, but only if it is possible to use numbers with infinite precision. I'm using floating point numbers for my calculations and rounding errors might creep in. Testing equality to zero has the potential to fail. Instead I test to make sure the absolute value of the error is less than a very small value.

So now we have our first optimization/pruning. We permute all combinations of three points then, before we go any further, test to see if these points are co-linear, if they are we skip them, if they are not, we calculate the coordinates of the circle that passes through them.

Me too, me too

There's a good chance that the circle that passes through three points will also pass through other points on the grid.

This is pretty easy to test. We know the origin of the circle and the radius, so we can then test each of the other points to see if it is also a distance r away from the origin (again respecting that there could be floating point rounding errors).

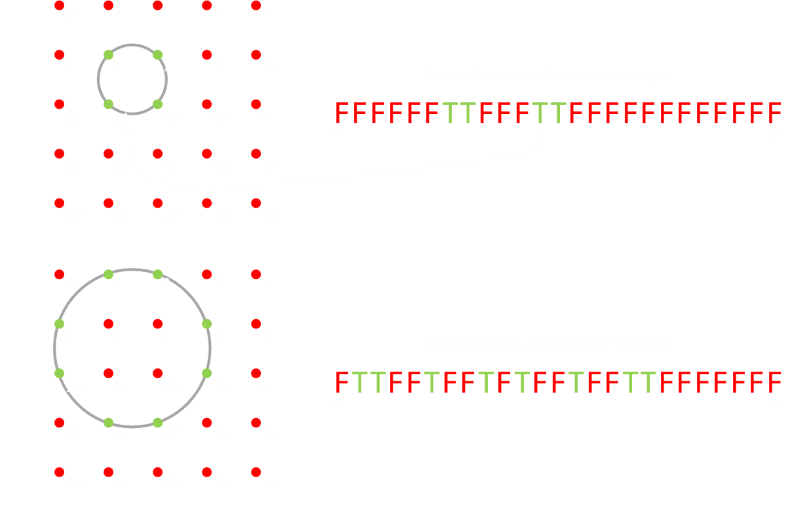
What we'll end up with is a collection of circles (x,y,r) and for each of these circles a boolean indicator if the circle passes through each of the points on the grid. A couple of examples are shown below (To help identify them, I've given each point a numeric index):

What you see from this is that we'll get a lot of duplication of the circles. We're defining our circles by just three points, but these circles may pass through other points, then as the loop passes through these later points they will, of course, pass through the earlier ones (to make an equivalent circle). Here comes another optimization. After generating all circles we can de-dupe to give a distinct set of circles, each with their unique boolean strings. We only need one definition for each circle that passes through three or more points.

Final step

We now have a de-duped set of all possible circles that pass through all combinations of three points. All we need to do is group five of them together and test to see if every point is passed through.

Again we can do this with nested loops. This time there are five loops; one for each circle. This is pretty brutal, and certainly the most intensive part of the solution calculation. Again, however, there are few earlier-bail optimizations we can apply. As we go along, getting deeper into the nested loop, we keep a track of the number of points we've successfully already pased through (performed by using a logical OR operation on the boolean strings and counting the number of 'true' bits). If the circle to be added does not increase the number of points passed through, we can instantly reject it (all it is doing is duplicating points already passed through with earlier circles; it's adding no value and might as well not be used).

Similarly, as we get towards the inner loop we can bail early if the number of running total of points is not high enough. The most number of points that any circle can contain in this geometry is eight, and this is the maximum number of virgin points that can be added with each step. So, if we arrive with just one circle to go and have less than (25-8) points passed through, we can immediately stop as there is no possible choice of circle that will get all 25 points. (We can go back even further; if we get to the point where there are just two circles left to be chosen as we have less than (25-16) points currently, then again we can bail).

Results

I generated 84 solutions to this problem (I did not duplicate for reflections or rotations). You can view these solutions in the app below. Use the buttons in the top right (or the left/right cursor keys on your keyboard) to scroll through them.

In the lower left corner are strings for each of the five circles showing which nodes each of the circles passes through. A "1" corresponds to true, and "0" to false.

The three buttons on the left allow you to toggle on labels for the grid nodes, turning the circles into distinct coloured circles (so you can differentiate them), and also for adjusting the size of each node based on its "Valence".

Valence is the number of circles that pass through each node, and when enabled, the node is rendered (semi-transparently) proportional to the valence.

Conclusion

I enjoyed this puzzle. It's the kind of puzzle that it's fun to write code to solve. I don't think it would have been as fun to solve with a piece of paper as it's hard to draw perfect circles. As you look at some of the solutions, some are fairly obvious looking, but others are weird* and I'm pretty sure some of them would have been missed if this problem were attempted 'by hand'.

*Solutions in which the origin of the circle is outside the grid and/or have large radii.

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.