
	Advertisement

Bounding Boxes

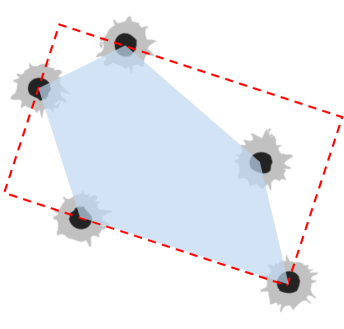
If you have a collection of points on a 2D plane, what is the most efficient way to draw a rectangular box around them?

Maybe there is a series of bullet holes on your wall and you want to cut out a rectangular piece of the wall and replace it with a new section of dry-wall? If dry-wall is sold purely by area, what is the cheapest way to do this with a rectangular replacement piece?

Maybe these a grease spots on a plain carpet, and you want to out find out the smallest rectangular piece of carpet you can cut out and replace?

These types of problems are appropriately called ’Bounding Box’ calculation problems.

Simple approach

A naïve approach might entail imagining these points on a Cartesian grid. Then, by simply taking the smallest the small and largest x-coordinates seen (minimum and maximum), and then repeating in the y-plane, the range of points in each axis can be determined and the box drawn using this parameters.

This will certainly produce a rectangular bounding box, and it is trivially quick to calculate. The bounding box it produces is orthogonal to the axes and this has many great and useful properties (especially in computers, whose displays are typically mapped using a Cartesian grid).

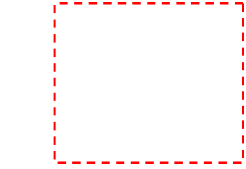A very fast, first order ‘hit-detection’ algorithm employs this strategy. If you want to see if a point is, potentially, inside a complex shape then you can quickly check the shape’s bounding box. If the test coordinate in question is outside the rectangular bounding box it is impossible for that point to be inside the shape and you can stop here before wasting time attempting the more complete and complex geometry calculations for inclusion.

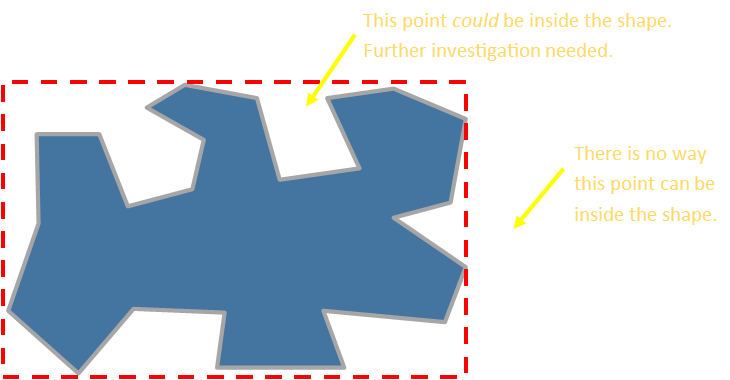
Arbitrary Angle Bounding Box

An axis-aligned bounding box is very useful tool, but only in certain simple cases is this the minimum area bounding box. If we are allowed to rotate the bounding box to any arbitrary angle, we can find a rectangle that has an area that it smaller. For instance on the same set of points:

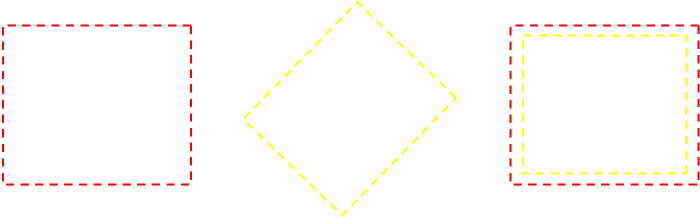
You can see that the yellow rectangle here has a smaller area.

So how do we go about calculating this optimal bounding box? Well, we could simply try test fitting rectangles until we got the correct one (Starting at 0° and incrementing the angle at the resolution we desired up to 90°. For each angle, we could rotate the coordinate frame and calculate the new axis-aligned box at this angle, and record the minimum area found).

This would certainly work, but there are some computationally less intensive (and more elegant) algorithms we can use (and these will give exact answers, not ones arbitrarily based on the resolution of angle sweep).

Before we get there, we need a little more theory …

Convex Hulls

It has been shown (H.Freeman, R.Shapira. Determining the Minimum-Area Encasing Rectangle for an Arbitrary Closed Curve, 1975) that the minimum area rectangle of a set of points is collinear with one of the edges of the collection's convex hull polygon.

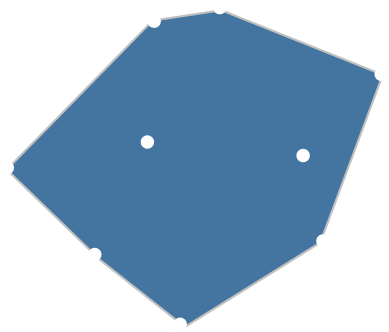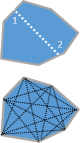
A Convex Hull is the smallest polygon that encloses all the points where all internal angles are less than 180°.

The easiest way to imagine this is to think about all the points as being pins sticking up on a board and you wrapping an elastic band over the pins. The shape of the rubber band is the convex hull of the points. Other people describe the generation as like winding a ribbon around the pins.

(It’s possible to generate convex hulls in dimensions more than two. In three dimensions, imagine covering up the object in tight gift wrapping paper)

There are various algorithms for determining the convex hull. One of the easiest to imagine is analogous to a lighthouse beam of light sweeping around. Starting at point known to be on the edge (such as the lowest y-coordinate) you can sweep a beam of light around until you touch the first point, then add this connecting edge to the hull and move to this new point, continuing your sweep around, and around, until you reach the next point …

Interestingly, the convex hull of a series of points is the polygon that has the absolute smallest area (with the restriction that all internal angles are less than 180°)

Think of a convex hull as only have 'bulges' and no 'indents'.

If you were able to cut a piece of dry-wall with arbitrary angles you could repair your bullet holes with a smaller area replacement shape than even the arbitrary rectangle by cutting a convex hull shape.

Also, because all the internal angles of a convex hull are less than 180°, it will be easy to make the cuts with your band saw or table saw with one pass for each edge! (concave cuts require sawing from two different directions)

There are some other interesting facts about convex hulls:

Any line drawn through a convex hull will intersect the polygon edge exactly twice (dividing the shape into two smaller convex pieces).
All diagonals (lines connecting any pair of vertices), lie entirely inside the hull.
Using the above, the sum of the internal angles is easy to calculate by selecting a vertex and radiating out diagonals to make triangles. The sum of the internal angles of a convex hull with n corners is = 180° x (n - 2)

Calliper algorithm

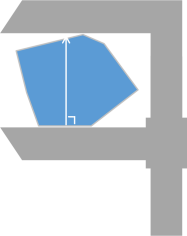
Now we have all the pieces we need for our algorithm.

We know that (at least) one of the edges of the a bounding box must be collinear with the convex hull of the points, so all we need to do is rotate the convex hull onto each of its edges and measure the perpendicular distance to the opposite side.

Imagine placing the polygon between the teeth of a pair of callipers. You measure the perpendicular distance from the edge being tested (and the corresponding horizontal distance), multiply these to get the area, then rotate the shape one edge and try repeat.

After you have tried all the edges you will know which rectangle gives the lowest area, and thus what is the optimal bounding box.

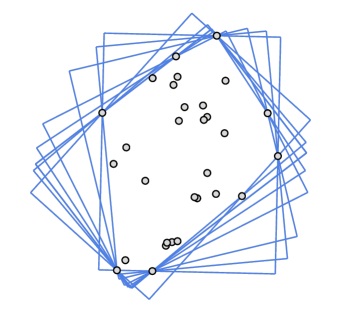There will be one potential rectangle for every edge on the convex hull. Depending on the geometry, the areas of many of the potential rectangles can be very similar.

Even without reading the technical paper referenced above, it's easy to see in your mind how the edge of convex hull and the bounding box must be collinear. Think about the shape in the calliper, with it flat on one edge. If you imagine trying to rotate the shape in the callipers, to turn it clockwise or counter-clockwise, the calliper will need to move up to make room for one of the corners, that was flush on the bottom, to rotate.

NOTE: There is a slightly different, but very similar, calculation sometimes used. This is the calculation of the shortest perimeter of the bounding box. The calliper algorithm is still used to generate the potential rectangles, but instead of minimizing the product of the two axes, we minimize the sum.

When might this minimum perimeter be useful? Well, imagine your bullet holes were in metal and not dry-wall. To repair this, you might need to weld in the replacement rectangle of metal. If you had free spare replacement material on hand, your costs would be purely for the welding. As welding is charged per linear foot, you could use perimeter minimization to reduce your welding costs.

Let's try it out (interactive demonstration)

Use the grid below to add points by clicking. When you have three of more points, you can use the buttons (or corresponding keys) to toggle on or off display of the convex hull or the arbitrary angle bounding box.

You can keep adding points to the collection even after the polygons have been calculated, and this will trigger a recalculation. Press 'C' to clear and start over.

Those blessed with a right mouse button can also use this to interactively delete a point.

That was fun!

Video Gaming

The concept of bounding boxes and convex hulls have a lot of applications in video gaming. If you two ships are flying towards each other you'd really like to know if they collide.

If you relied purely on axis aligned bounding boxes, your game would not be popular!

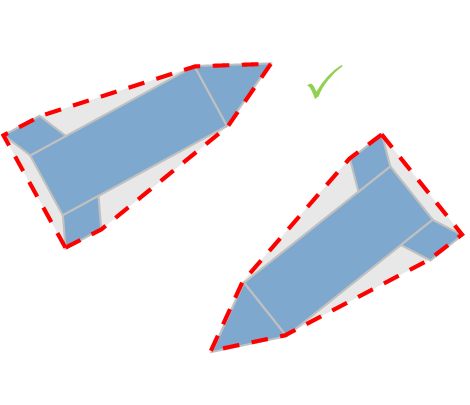Here are the same two ships drawn showing their convex hulls and arbitrary bounding rectangles.

If you enjoyed this article, you might like this one which talks about linear regression and how to calculate best fit straight lines.

This article describes how to elegantly rotate an image using just a collection is shear operations.

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.