Grazing and Calculus
Old MacDonald had a farm. On that farm was a big field.

One day, Farmer MacDonald wanted to section off part of this field to create a paddock for his goat.
To partition off the paddock, the farmer had some straight sections of fencing. If he wanted to make a rectangular shaped paddock, what is the optimal shape? For a fixed length of fencing (perimeter), what shape creates the largest internal area of grass which the goat can graze upon?

|
What is the optimal shape for a rectangular field? |
Diagram

|
Here's a diagram of a generic rectangular field. We'll define the perimeter of field (the length of the fence) to be L The length of the horizontal sides of the field we'll define as x. Similarly, the length of the vertical sides to be y. |
The perimeter of fence is simply twice that of the lengths of each side. We can re-arrange this to get an equation for y based on the length of the fence and the width:
The area of the field is the product of the height and width. From above we can substitute in the height:
Keeping the length of the fence (L) fixed we can differentiate the area with respect to the width of the field. Setting this to zero determines the turning point (Differentiating a second time reveals a negative value, confirming the turning point is a maximum value). This gives us the result we need.
We have shown that, to maximize the area for a fixed lengh of fence, that both sides of the paddock need to be the same, and a quarter of the length of the fence i.e. The field will be square!
The optimal field is a square.
Enter the Barn
|
In old MacDonald's field, there is also a big square barn. Farmer MacDonald is pretty smart. He realizes that he can use the wall of the barn to form one edge of his paddock. This will allow him to give his favourite goat more grass to graze over using the same length of fence. If we assume (for now) that the side of the barn is much longer than any side of the paddock needs to be, what is the optimal shape now? |
|
Here's a diagram of the modified paddock. As before, the length of the fence is L The length of the horizontal sides of the field we'll define as x. The length of the single vertical sides is y. |
|
As before, we can create a formula for the area in terms of L, x, then differentiate with respect to x, and set this to zero to find the turning point. The math is very similar to before:
And here we have the result:

What this tells us is that, for optimal area, the field should be twice twice as long in the direction parallel to the barn, and half as long in the width. This makes sense on multiple common sense levels: It's maximizing the 'free' fence created by the wall, and from symmetery it's a square cut in half. We know that the square is optimal if we have fences all the way around, and all we are doing with the barn wall is dividing a square field in two.
Different Size Barn
What happens if the length of the barn is shorter than one of the sides of the paddock? This is much more interesting puzzle.
We can think of this in two ways. The first (shown on the left), is with the fence line being flush the side of the barn. The second (shown on the right) is with the barn jutting into the field.
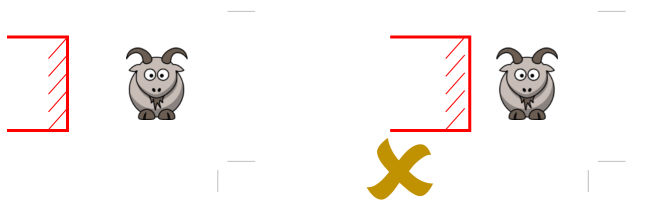
I think it's fairly obvious that the situation on the right cannot be optimal. It's the same length of fence as the diagram on the left, but any encroachment by the barn into the paddock reduces field area with no benefit.
Let's get to the math. We'll define the length of the barn to be b.
Now we have the equation for the height (y) we can place this in the formula for the area:
Differentiating this and setting to zero allows us to determine the optimal values for x and y:
The result should not be a surprise. Again we have a square (we already know a square is optimal, so it should not matter if some of the contribution for the perimeter comes from the barn or the farmers fence).
We have a formula for the area of this hybrid paddock, and this is shown below:
It does not matter where the barn fits on the side, as long as it is shorter than the length of the side.
But what if you are biased?
Hold on, hold on, not so fast. We've seen that barn contributes 'free' fence to the paddock. Shouldn't we try and get the barn to contribute as much to the perimeter as possible? We mentioned earlier that barn was square, and high school geometry educated us that the diagonal of a square is longer than the sides by a factor of √2
Is it better to construct the paddock on a bias? By building at 45° we'll have the maximium possible length of barn in the perimeter. The downside is that the corner of the barn will have eaten into some of the area of the paddock and we'll have a triangle of potential grazing area removed. Is this significant? Let's take a look …
|
Here the square barn forms part of one side on the bias. The length of the perimeter contributed by the barn is √2b. The loss of paddock from the corner of the barn is very easy to calculate. It's simply half the area of the barn. |
The length of the perimeter fence needed is reduced by the diagonal of the barn.
The area of the paddock, this time, is reduced by the area of the triangle of the barn.
Differntiating, setting to zero, and solving gives the dimensions of the optimal paddock. Again it's a square.
Finally, the area of this paddock is can be described by this formula:
Which is bigger?
We have two different equations for the area of the paddock. The first when the barn is parallel, and the second when it is on a bias. By substracting them we can work out the delta.
And here we have the (fascinating) result. There is an inflection point. If the barn is small compared to the overall perimeter of the paddock, it is better to build it on a bias. If the barn is large compared to the perimeter, then is it better to build the paddock parallel to the barn.
We can calculate the inflection point and this is when the ratio of L/b is shown below. At this point, the paddocks will have the same area irrespective of either of two orientations of the barn.
Using this value we can determine the x and y values of the square paddocks. Here are their values:
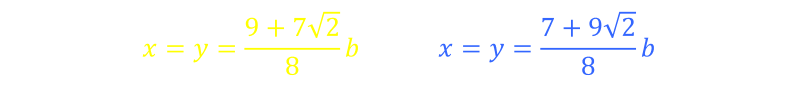
Here are renderings of these values to scale (showing equal grazing areas):

If the perimeter is long, bias is better. If the perimeter is short, parallel is better.
Don't be square
What would happen if farmer MacDonald was not restricted to making rectangular fields? How about an octaganol field?

|
Here's a diagram of a regular 8-sided paddock. How about if we make it a 10-sided paddock? To solve these we need a way to work out the area of a regular n-sided polygon. |
|
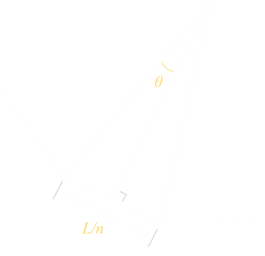
To the right is a picture of a generic n-sided polygon. The length of each side of the paddock is the total perimeter divided by the number of sides. Because we know the number of sides we can calculate the angle θ. There are 360° in a circle (2π radians), and the angle shown is half of this angle. The perpendicular line connecting the center of the polygon to the mid-point of any side is given a special name, it is called an apothem. As the polygon is regular, these are all congruent. (If a circle were to be inscribed inside the polygon, the apothem would be the circle radius). The area of the entire polygon is the sum of the n congruent triangles; the indivuidual triangles' areas can be calculated by multiplying the apothem by half the length of one of the sides (area of trianlge is half the base, multiplied by vertical height). |
|
|
As the number of sides increases, the area of the enclosed paddock asymptotes. To the left in tabular form are the number of sides, the length of each side, and the apothem and the area for various n-sided polygons each with unit length perimeter. This data is also plotted in the chart below: 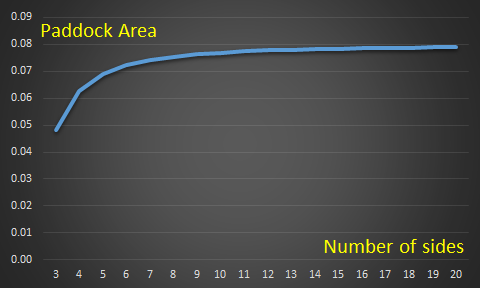
|
As the number of sides increases, the polygon gets more and more circular. (Proving what we already inutively know; that a circular fence encloses the largest area of field of the length of fence). As n increases, the area gets closer to 1/(4π). A circular field is 27% more efficient than a square field (but does not tesselate, so has plenty of other disadvantges).


UPDATE - See here for an update.
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.

