The Beauty in Mathematics
Today I’m going to look at some of the charming applications of a clever piece of mathematics. It relates to a conundrum first posed in the 17th century, and was not fully solved until the invention of Calculus. It’s a simple problem with some startling results.
Let’s start our investigation with a rhetorical question: What’s the shortest distance between two points?
What is the shortest distance between point A and point B in the diagram below?

I hope you’ll quickly be able to answer that it’s a straight line*
*We’re dealing exclusively with Euclidean geometry here. No tricks, gotchas, or distorted coordinate frames!
Bead on a wire
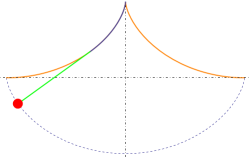
We’re now ready to pose the question that the rest of this article will discuss: If these two points are vertically separated, what is the quickest way to get from between point A to point B?
i.e. If we connected the points with a stiff wire, onto which was threaded a small bead, what shape would the wire need to be get the bead to the finish in the shortest period of time?

The bead will accelerate down the wire because of gravity (we are going to ignore friction and air resistance). Constrained by the wire, which bead will get to the bottom first? Think about it for a minute or two:
Will the bead that zips down a straight wire finish first? After all, we know that this is the shortest distance between the two points, so the distance that the bead needs to travel is at a minimum. Also, the bead does not need to change direction or be deviated from it's initial descent vector.
Will the bead the runs along a parabola finish first? A parabolic curve, being proportional to vertical displacement squared, more naturally represents an object falling under gravity (In fact, this is the flight profile that those 'vomit commit' zero-gravity experience flights take when they give people the feeling of weightlessness).
Will the bead that follows some kind of ski-jump profile curve finish first? This curve has the advantage of a steep initial drop to build up the speed, then, when the speed is higher, transitions this into the horizontal section to cover this distance in a shorter time.
Does it not make a difference what path is taken? After all, surely this is a conservation of energy thing? The same gravitational potential energy (difference in height), is converted into the same amount of kinetic energy, so it should not matter what path is taken?
Or, will is be none of these, and be something different still, such a quarter circular path? There is natural symmetry in a circular arc, and this has a constant radius of curvature.
All very plausible sounding arguments! What do you think the solution is? Place your bets …
Newton, Bernoulli, Huygens, Leibniz, von Tshirnhau, l'Hôpital
In the late 17th Century, some of the smartest mathematicians that have ever lived: Newton, Bernoulli, Huygens, Leibniz, von Tschirnhaus, l'Hôpital… worked on this problem, solving it in a variety of ways and at different speeds, based on a challenge thrown down by Bernoulli's brother:
“I, Johann Bernoulli, address the most brilliant mathematicians in the world. Nothing is more attractive to intelligent people than an honest, challenging problem, whose possible solution will bestow fame and remain as a lasting monument. Following the example set by Pascal, Fermat, etc., I hope to gain the gratitude of the whole scientific community by placing before the finest mathematicians of our time a problem which will test their methods and the strength of their intellect. If someone communicates to me the solution of the proposed problem, I shall publicly declare him worthy of praise.”
History records Newton as solving it the fastest. Just a few decades earlier Galileo*, without the benefit of Calculus, looked at this problem and got the incorrect answer, so don't feel bad if you miss it too!
Brachistochrone curve
There is an optimal solution to this problem, and the path that describes this curve of fastest descent is given the name Brachistochrone curve (after the Greek for shortest 'brachistos' and time 'chronos'). Brachistochrone might be a bit of a mouthful, but count your blessings, as Leibniz wanted to call it a Tachystoptote curve! (from swiftess 'tachystos' and piptein 'to fall')
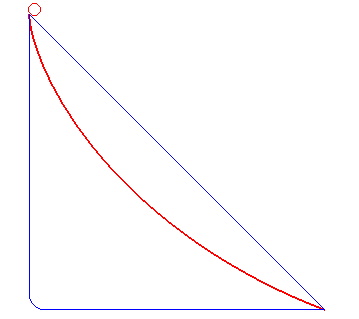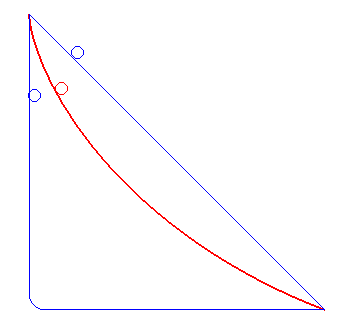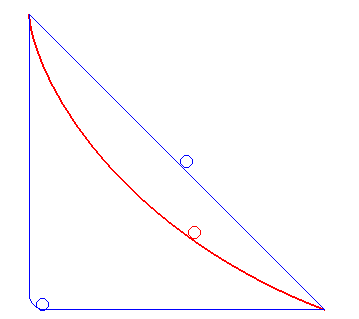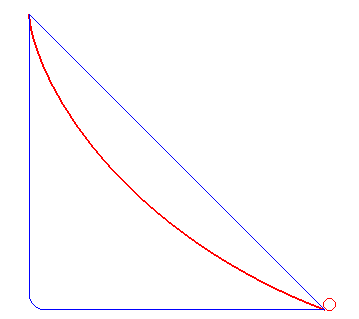 Image Credit: Robert FERRÉOL |
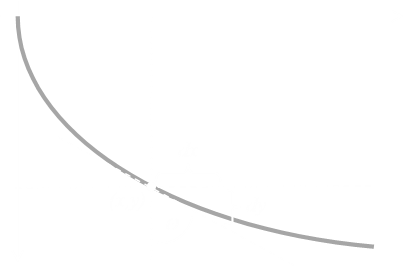
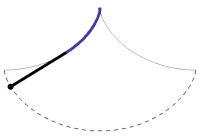
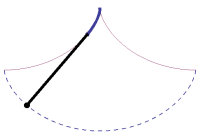
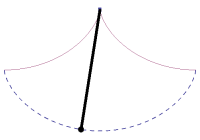
The actual shape of a Brachistrochrone curve is closest to the 'ski-jump' curve drawn above, and the explanation given in the bullet point is correct. A near vertical drop at the beginning builds up the speed of the bead very quickly so that it is able to cover the horizontal distance faster to result in an average speed that is the quickest. Decreasing the initial angle (closer to the straight line), increases the total time, as does a long verticle drop (even at the limit of allowing the ball to pretty much fall vertically until the last second, then travelling horizontally). The animation on the left shows a Brachistochrone path in red, and two other possible paths in blue with representations of balls rolling down tracks. *(Galileo concluded, incorrectly, that a circular path was the quickest descent path). |
Calculus of Variations
To calculate the optimal path does not just require vanilla calculus (where you are minimizing a variable in a function), but instead requires minimizing a function that minimizes some other variables. This is the calculus of variations. There are many excellent papers available that walk through the process, so I'll race through things very quickly here. The internet is your friend if you need a more detailed explanation.
|
The basis if the calculation is about the conservation of energy. The potential energy lost by the falling bead (in the vertical plane), is converted into kinetic energy. If we measure the distance along the arc as s, and an infinitely small piece as ds, then: 
|
Different paths will have different functions for how the gradient changes. The goal is to find the minimum functional of y.
We know the path is continuous (no gaps, and no instantaneous changes in velocity), and we know there is an acceleration term, so there will be a non-zero second derivative d2y/dx2, and we know the two values for the endpoints.
Cutting to the chase, here is the result. It's a pair of parametric equations for the x and y coordinates in w.r.t θ

Where K is a constant scaled to make sure the curve passes through the end point ( xB , yB )
Cycloid
Here is our first amazing result. The above parametric equations describe a curve called a Cycloid.
This is the path traced out a point on a circle is it rolls along a straight edge.
Imagine a coloured dots painted on the rim of a wheel that rolls past you. The path of fastest descent follows the shape of a cycloid curve for 0 ≤ θ ≤ π. Initially the descent is vertical, rounding out to horizontal.
Implications
 Image Credit: Jason Karsh Image Credit: Jason Karsh |
Brachistochrone curves are useful for engineers and designers of roller coasters. These people might have a need to accelerate the car to the highest speed possible in the shortest possible vertical drop. As we have just proved, the Brachistochrone path is the quickest way to get between two points. |
|
There are implications in sports too. If you are a downhill skier, and aiming for a fast time, you don't necessarily want to take the path between two points that is the shortest distance, but instead a path that will get you there the quickest! Surfers wanting execute a cutback will appreciate the extra speed gained from riding down a wave if they surf down a Brachistochrone. |
 Image Credit: Giuseppe Broccolo Image Credit: Giuseppe Broccolo |
Further down the rabbit hole …
|
Things get even more amazing! In a uniform gravitational field, a brachistrochrone path is also something called a tautochrone (Again, from Greek, taut meaning 'same'). An object can be place anywhere on a tautochrone, and it will slide to the end point in the same amount of time! Objects placed near the top will travel faster past the finish line than objects placed near the bottom, but all will finish at the same time. (The actual time taken is π times the square root of the the radius of the cycloid over the acceleration of gravity). |
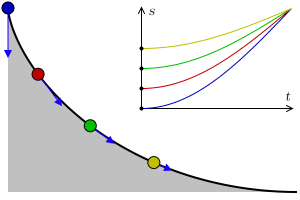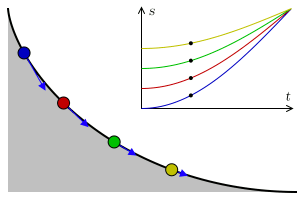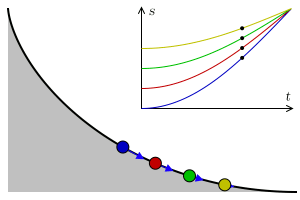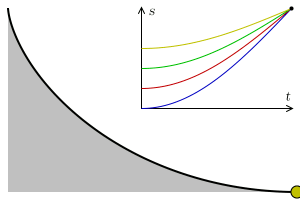 Image: Geek3 Image: Geek3 |
 |
Balls place on cycloid shaped ramp will roll backwards and forwards with the same frequency. It does not matter where on the ramp the ball is initially placed, it will complete a round trip in the same time.
There's a nice interactive animation of this as a Wolfram Demonstrations Project. Remembering back to high-school physics, the period of a pendulum is determined by it's length, but this is an approximation. As the pendulum swings, it's height changes. This is very small when the pendulum is long and the subtended angle of the swing small (see diagram on left), but there is an error component. This error was investigated by Huygens who proposed using the involute of an inverted cycloid (we'll explain exactly what that means shortly), to make a perfect pendulum. He is the first to consider suspending the string of the pendulum at the cusp on an inverted cycloid. |
|
If the length of the pendulum is created to make it half the arc length of the cycloid, then the mass at the end will trace a cycloidic path a thus swing with the same time period irrespective of the amplitude of the swing. The word Involute is used to describe the locus of a point considered at the end of a taut string being wound and unwound around an entity. One of Huygen's drawings of such a pendulum clock is shown below. The curves of metal at the top of the pendulum are now, affectionately, known as Huygen's Chops. |
|

As the pendulum swings, the string rides down the side of the chops. The involute of an inverse cycloid (the shape of the chops) traces out a barichstochrone.
 |
 |
 |
 |
Cycloids, Brachistochrones, Tautochrones
The cycloid's unique property is mentioned in the following passage from Herman Melville's Moby Dick:
|
If you set-up your childrens' model race track with a brachistochrone shaped start ramp, then you could educate them that it is not important where on the curve they start their cars for a fair race. 
(Of course, kids will tell you that red cars always go faster!) |
 Image: Leszek Leszczynski Image: Leszek Leszczynski |
 Image: Jon Pinder Image: Jon Pinder
|
A mathematically perfect skate park bowl should have sides that are shaped as a tautochrone. If you collide with someone on one of these, you can rest assured that everyone, and their equipment will get to a pile at the bottom of the hill at the same time! If your bowl is not a perfect tautochrone, depending on the shape, it might even by possible to impress your friends by being able to faster than they can by, paradoxically, (to them) not pointing your board directly down the slope, but by taking a path that traces out the brachistochrone. |
|
As I understand it, there is no defined standard for ski-jump profiles (many being built-into the surrounding terrain and using the natural gradient), but if you were going to construct one, you could give it a brachistochronic profile. A bonus of this is that it you could enter the ramp at any point of the curve, and it would take the same amount of time before you flew off the edge. By slowly working your way up the ramp you could gradually increase your exit speed whilst keeping your 'slope time' a constant. The image on the right shows the jumps at Lake Placid. |
 Image: lifecreations Image: lifecreations
|
The return of the Involute
|
To balance things out, it's worth mentioning that, as cool as cycloids are, sometimes there is a better tool for the job. Gearing is one example. Early gears were made with cycloidal designed teeth. Whilst cycloid gears typically have wider flanks than other designs, and thus slightly stronger (at the same pitch), they are not often used in modern machinery. Cycloid gears are constructed with two cycloids. In the animation to the right you can see the outer circle rolling to trace the 'face' of the gear tooth, whilst the inner circle traces the 'flank'. The resultant basic shape may remind you of a bicycle sprocket (which is where it is still commonly used). This animation continues, and draws radial lines to show removal of addition flank material. This additional reduction is performed for clock gears (reducing weight and, more importantly, to reduce contact and friction). |
 Image: Gary's Clocks Image: Gary's Clocks |
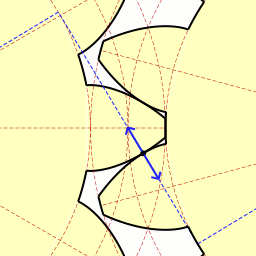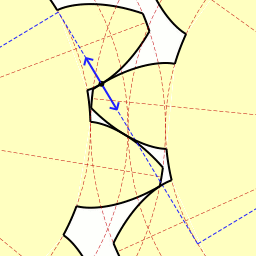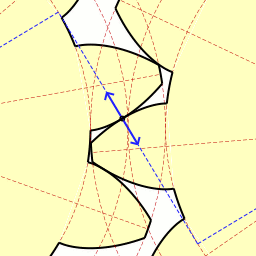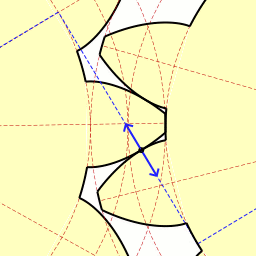 Image: Claudio Rocchini Image: Claudio Rocchini |
Today, most gears are designed with an involute pattern. (Sort of like imagining a gear wheel manufactured with a whole set of teeth like Huygen's Chops! The relative rates of rotation the involute gears are constant while the teeth are engaged, and also, the gears always make contact along a single steady line of force. With teeth of other shapes, the relative speeds and forces rise and fall as successive teeth engage, resulting in vibration, noise, and excessive wear. Within reason, the distance between the centers of two meshed involute gears can be varied without changing the velocity ratio of the two wheels. (Cycloidal gears require an exact distance). Finally, involute gears are easier to manufacture having flat tops and bottoms, with just curved sides. |
Cycloidal gears are still seen in watches, clocks and chain drives, but pretty much everywhere else uses involute gears these days.
A rolling stone
Next time you have to roll a stone down a hill, I hope you'll remember those 17th Century mathematicians!
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.

 Image: David Darling
Image: David Darling Image:
Image: 