Pi, PINs and Permutations
|
This article builds on ideas written about in three earlier blog posting: Pi, Passwords (specifically PIN numbers), and De Bruijn sequences. Ingredient 1: In 2013 I wrote an article about how “spectacularly unimaginative” people are when selecting their passwords. I even got asked to turn this into a TEDx talk (which was a fantastic and humbling experience). |
 |
 Photo Credit: Jessica Snow
Photo Credit: Jessica Snow
 |
Ingredient 2: A little earlier, I’d preformed some whimsical analysis on the digits of Pi. What I was trying to show was that, if you look hard enough (and long enough), you can find anything you want in the digits of Pi (probably). Your age, your phone number, your street address, your social security number … … even your ATM card PIN! |
|
Ingredient 3: De Bruijn sequences. Using the same principles I demonstrating with De Bruijn sequences (using a sliding window of contiguous digits), I was curious how many digits of Pi would you need so that every four digit PIN would be encountered at least once. |
 |
 |
If we contrived an automated machine with a robot arm, and fed it Pi, how many key presses would it need (worst case) to go through all possible four digit PINs? (And, out of curiosity, What would be that last PIN? Which of the 10,000 four digit permutations occurs last in Pi?) The first four digit PIN is 1415, as these are the first four digits in the decimal representation. |
|
The next is 4159 … and so on … 5358 is the eighth seen … Each time we move the slider along we encounter a PIN that comprises three digits from the last PIN (shifted left), plus a new digit on the end. Obviously, there will be some repetition. In fact the first repetition occurs very early on. The digits 0582 occur in position #50, then shortly afterwards in position #132. |
 |
Results
Here is a scatter plot of the results. On the x-axis we have each of the PINS (from 0000 on the left to 9999 on the right). The y-axis shows at what position in the decimal digits this PIN first occurs at.
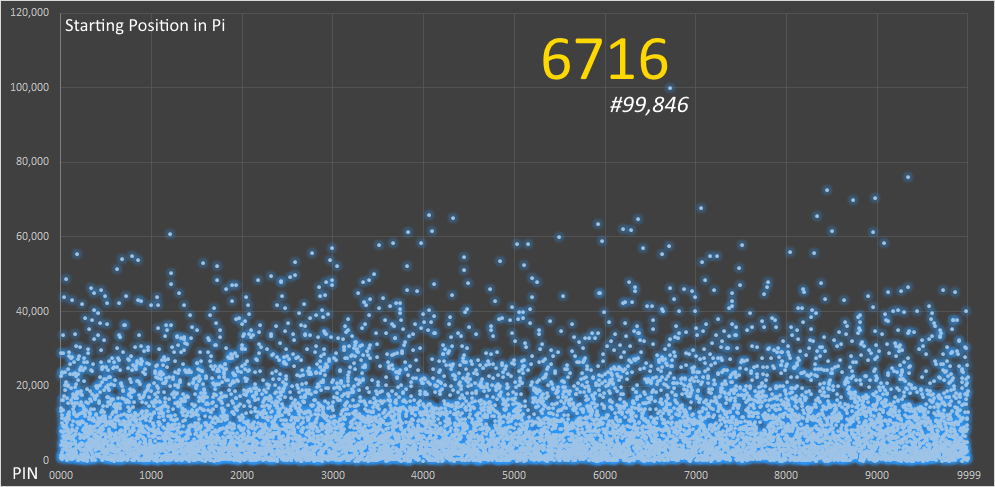
Interestingly, there is one massive outlayer, and this is the PIN 6716. This occurs first starting at digit position #99,846.
So, to be sure of getting every four digit password, then Pi to at least 99,847 digits is needed (strictly speaking 99,848 digits, as the digit following the last one is a six, and without an extra digit of precision it would get round up!)
(The shortest possible arrangement of digits is 10,003 characters).
Five Digits
If we expand the analysis to five digit PINs, then the furthest distance discrete PIN is 33394 which occurs way out at #1,369,560.
Six Digits
For six digit PINs, the furthest distance discrete PIN is 569540 which occurs way out at #14,118,307.
Jenny
If you are looking for when 8675309 occurs, than I'm pleased to tell you it first appears at position #9,202,591 of Pi.
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.

