Home Blog About Us Work we do Content Contact Us
 

Newsletter: Click here to join an email list and be contacted when a new article is published.

 

 

 Advertisement 

Compound interest and retirement

“The money that money earns, earns money”
- Ben Franklin

I’ve written about the terrific power of compound interest before. The previous article was little more math heavy, feel free to read it for some more background, but in this article I want to focus on one simple, illustrative, example.

Retirement Investment

I hope you are all contributing, fully, to your retirement plans?

Here’s an illustration showing just how important it is to start investing early.

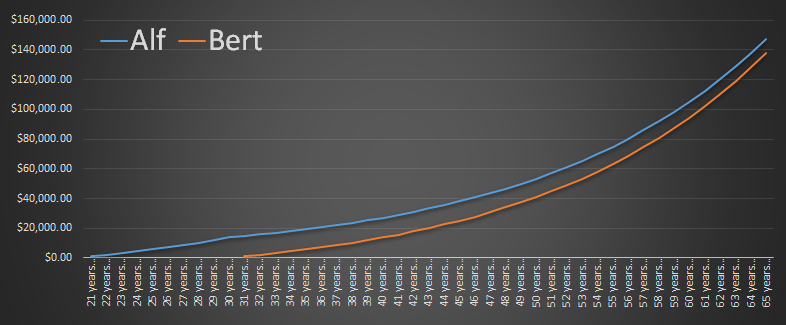
Imagine there are twin friends, Alf and Bert. Both get the same job, earning the same salary. Both start their working lives at age 21, and both plan to retire at 65.

Who will end up with more money?

Question: If we assume an annual return on investment of 7% a year, which friend ends up with the most in their retirement fund at 65?


Image: gfpeck
Image: Images of Money

The startling fact is that, despite only making ten payments, Alf will retire with more money than Bert!

To get equal, Bert would have to continue working, and paying $1,000/year, until he was 81 years old, just to reach the same investment as Alf’s, needing 70 more payments!

Please don’t take the wrong thing away from this lesson! The lesson is NOT that you should invest, then stop! The fiscally prudent thing to do would be for both friends to make continuous deposits. The lesson is that, if you start late, you’re unlikely to catch up (and you’ll end up having to put much more down at the end). Remember “The money that money earns, earns money”.

Data

Below is the raw data in tabular form. The balance is calculated by adding to the current deposit to the previous balance after that is grown 7%. On the left is Alf's deposits and balance. On the right is Berts.

ALF
AgeDepositBalance
21 years old$1,000.00$1,000.00
22 years old$1,000.00$2,070.00
23 years old$1,000.00$3,214.90
24 years old$1,000.00$4,439.94
25 years old$1,000.00$5,750.74
26 years old$1,000.00$7,153.29
27 years old$1,000.00$8,654.02
28 years old$1,000.00$10,259.80
29 years old$1,000.00$11,977.99
30 years old$1,000.00$13,816.45
31 years old$0.00$14,783.60
32 years old$0.00$15,818.45
33 years old$0.00$16,925.74
34 years old$0.00$18,110.54
35 years old$0.00$19,378.28
36 years old$0.00$20,734.76
37 years old$0.00$22,186.20
38 years old$0.00$23,739.23
39 years old$0.00$25,400.98
40 years old$0.00$27,179.04
41 years old$0.00$29,081.58
42 years old$0.00$31,117.29
43 years old$0.00$33,295.50
44 years old$0.00$35,626.18
45 years old$0.00$38,120.02
46 years old$0.00$40,788.42
47 years old$0.00$43,643.61
48 years old$0.00$46,698.66
49 years old$0.00$49,967.56
50 years old$0.00$53,465.29
51 years old$0.00$57,207.86
52 years old$0.00$61,212.42
53 years old$0.00$65,497.28
54 years old$0.00$70,082.09
55 years old$0.00$74,987.84
56 years old$0.00$80,236.99
57 years old$0.00$85,853.58
58 years old$0.00$91,863.33
59 years old$0.00$98,293.76
60 years old$0.00$105,174.33
61 years old$0.00$112,536.53
62 years old$0.00$120,414.09
63 years old$0.00$128,843.07
64 years old$0.00$137,862.09
65 years old$0.00$147,512.43
BERT
AgeDepositBalance
21 years old$0.00$0.00
22 years old$0.00$0.00
23 years old$0.00$0.00
24 years old$0.00$0.00
25 years old$0.00$0.00
26 years old$0.00$0.00
27 years old$0.00$0.00
28 years old$0.00$0.00
29 years old$0.00$0.00
30 years old$0.00$0.00
31 years old$1,000.00$1,000.00
32 years old$1,000.00$2,070.00
33 years old$1,000.00$3,214.90
34 years old$1,000.00$4,439.94
35 years old$1,000.00$5,750.74
36 years old$1,000.00$7,153.29
37 years old$1,000.00$8,654.02
38 years old$1,000.00$10,259.80
39 years old$1,000.00$11,977.99
40 years old$1,000.00$13,816.45
41 years old$1,000.00$15,783.60
42 years old$1,000.00$17,888.45
43 years old$1,000.00$20,140.64
44 years old$1,000.00$22,550.49
45 years old$1,000.00$25,129.02
46 years old$1,000.00$27,888.05
47 years old$1,000.00$30,840.22
48 years old$1,000.00$33,999.03
49 years old$1,000.00$37,378.96
50 years old$1,000.00$40,995.49
51 years old$1,000.00$44,865.18
52 years old$1,000.00$49,005.74
53 years old$1,000.00$53,436.14
54 years old$1,000.00$58,176.67
55 years old$1,000.00$63,249.04
56 years old$1,000.00$68,676.47
57 years old$1,000.00$74,483.82
58 years old$1,000.00$80,697.69
59 years old$1,000.00$87,346.53
60 years old$1,000.00$94,460.79
61 years old$1,000.00$102,073.04
62 years old$1,000.00$110,218.15
63 years old$1,000.00$118,933.43
64 years old$1,000.00$128,258.76
65 years old$1,000.00$138,236.88

At 65 years old, Alf's investment would have compounded to $147,512.43, however Bert's would have reached only $138,236.88

The restaurant at the end of the Universe

If you need an amusing consequence of the power of compounding interest, you must read the second book in the comic series The Hitchhiker's Guide to the Galaxy, which describes Milliways, the restaurant at the end of the Universe, from which the book gets its title.

All you have to do is deposit one penny in a savings account in your own era, and when you arrive at the End of Time the operation of compound interest means that the fabulous cost of your meal has been paid for. This, many claim, is not merely impossible but clearly insane, which is why the advertising executives of the star system of Bastablon came up with this slogan: "If you've done six impossible things this morning, why not round it off with breakfast at Milliways, the Restaurant at the End of the Universe?" – Douglas Adams

Albert Einstein

Someone else who knew what he was talking about:

“The most powerful force in the universe is compound interest” – Albert Einstein

Make sure you start contributing to your retirement plan as soon as possible!

 

You can find a complete list of all the articles here.      Click here to receive email alerts on new articles.

© 2009-2018 DataGenetics    Privacy Policy