
	Advertisement

How tall is that tree?

How can you determine the approximate height of a tree without felling it?

There’s no single answer to this. There are lots of creative ways.

If it’s a sunny day, and the terrain around the tree is relatively flat (and open), you can compare shadows. If you know your own height, and have a tape measure, you can measure the length of your own shadow and then measure the length of the shadow cast by the tree. The ratio of your height to your shadow is the same as the ratio of the height of the tree to its shadow. It's a simple calculation.

What else can you do? Well, again, if the terrain around the tree is flat you can pace out from the tree a known distance and measure the angle to the top of the tree. Then, using a little trigonometry, you can estimate height (the tangent of the angle is height of the tree divided by the distance from the tree).

A slight complication of this estimation technique is that your eye is not directly at ground-level. Using a simple triangle, this would calculate height of the tree above your eye level. To get the true estimate of the tree you’d need to add this height back in. Even after correcting from this eye level offset, there are still two issues with this technique:

It does allow us to calculate the height of trees if the ground is uneven
(and/or if the base of the tree is higher/lower than the observer).
The technique requires both a tape measure and inclinometer (a tool for measuring the angle).

Is there a technique we can use that removes these limitations? If we can assume you know your height then, yes, there is.

There is a way to calculate the height of a tree without requiring a tape measure (using just angles), and this methond does not have the restriction that the base of the tree is at the same elevation as the observer.

Tangent Solution

The first thing you need to do is stand in front of the tree and mark your height on the trunk. You can do this with a piece of string, chalk, or even a yellow ribbon.

Then walk away from the tree to a location where you can see the top of the tree, the bottom, and ribbon. We don’t need to know the distance. Finally, we need to measure the angle to each of these points from the horizontal (or the vertical if you prefer, noting there is a 90° difference).

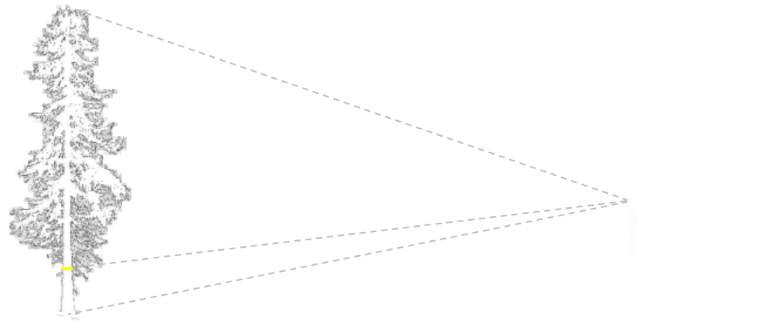
Care needs to be taken about the sign of the angles. Any of them can be above, or below, the horizon level. The beauty of mathematics, however, is that, if we are consistent with our signs, this does not matter.

We can see that (if we assume the tree is reasonably vertical), the angles form a collection of right angle triangles with the opposite edges forming parts of the spine of the tree. All we need to do now is create some simultaneous equations so that we can eliminate the perpendicular distance d we are standing away from the tree.

The key to doing this is that we marked our height on the tree and, therefore, we know the value of h_c.

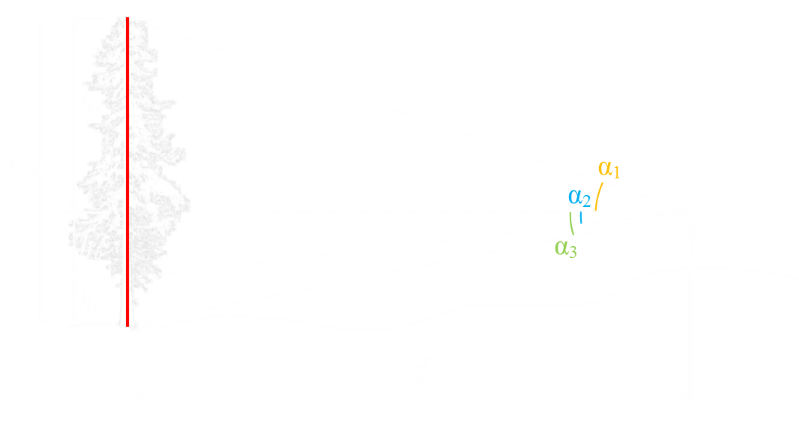
Math

From the three right-angle triangles, we can get get three equations for the components of the tree height based on the angle from the viewer and the distance between the two:

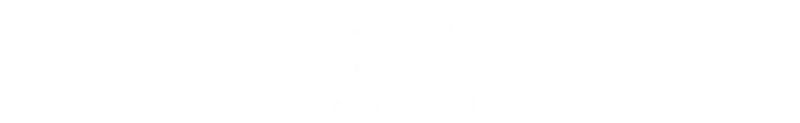
Combining the last two allows the derivation of an equation for the distance of the observer from the angles (known), and h_c (which is also known; this is the height of observer, as marked on the tree by the ribbon):

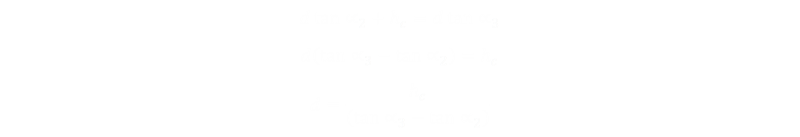
Finally, the total height of the three is the summation of the three component heights. because we know the distance d, we can substitute this in to give our final equlation:

Example

Imagine we take three measuresments: α₁ = 23°, α₂ = 5°, α₃ = 12° and you are 1.9m tall (6'3")

This would give an approximate height of the tree of 9.7m (31'10"), and you'd be observing the tree from the horizontal distance away of approx 15.2m (49'10").

Issues

Remember, this is just an approximate way to determine the height of a tree. There are lots of sources where inaccuracies can creep in: The tree might not be vertical. You might not be able to correctly sight the top of the tree (especially it the top canopy is broad). You have only finite precission to which you can measure angles …

All these things to one side, it's certainly a better way of doing it than chopping the tree down!

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.