
	Advertisement

Monsters with Laser Guns

Our monster trouble continues. (For background reading, check out these links below):

This time the monster, and nine of his friends, are chasing you around an underground cave complex. The monsters are all armed with single shot laser guns. The monsters are perfect shots on static targets, but can’t hit for toffee whilst you are running. Being very smart monsters they know this, so will not waste their single shot when you are moving; you are safe as long as you continue to run.

You can’t run forever, and you’re going to tire far quicker than the monsters. You need a plan to escape. Using your communication device you call up your ship, which is conveniently parked in orbit (did I mention this is a science fiction puzzle?), and arrange to be teleported out.

However, since you are deep underground, the transport room cannot ‘lock-on’ to you as a moving target and they inform you that you will need to stand still for a couple of seconds to allow them to safely get you away. You know that if you stop, zap!, the monsters will fire their lasers and you will be dead. This is not an option.

A better plan

You devise a cunning plan: Up ahead is a bend in the cave tunnel where you will be out of view for a fraction of a second. Not long enough for the transporter to lock on, but long enough for you to deploy the Ace up your sleeve.

In your pocket you are carrying a battery powered Holographic Replicator.

A Holographic Replicator will project out multiple copies of you to confuse the monsters.

Now you see me, now you see me, now …

The device you are carrying has a maximum setting of nine. You are going to run around the corner, press the button, and stand still (the holographic projector only works on static images). The monsters will come around the corner and see ten versions of you (One real you, and nine holographic copies).

Each monster will take aim at a random target, they will not communicate with each other, and they will all fire at the same time. ZAP!!!

If you’re hit by one (or more) of the lasers it is instant death. If all lasers miss you, the transporter will have enough time to lock-on to your location before the (even more angry) monsters can run up to you and maul you to certain death.

What is your chance of survival with this plan? (You can assume the holographic replicator is good enough that the monsters are unable to distinguish between the real you and a hollow you).

There are ten of ‘you’ and ten monsters. What are your chances of surviving the encounter?

Dependent or Independent events

Clearly, if the monsters could communicate and collaborate with each other it would be game over for you. The ‘first’ monster would fire at a the ‘first’ target of you, then the ‘second’ on the next … It really wouldn’t matter what ‘first’ or ‘second’ means, as long as each monster fires at a distinct (fresh) target then there is a certainty you would eventually be shot (assuming the number of monsters is ≥ than the number of images of you. A shot will either kill you, or reduce the number of locations you could be by one).

In this puzzle, you stand a chance of surviving, however, because of the lack of communication between the monsters. Each takes a random shot at one of the targets. There is a chance that more than one monster will fire at the same target. There is a chance that none of the monsters will fire at the target that is you. This is the probability we need to calculate.

Ten holographic bottles of beer on the wall

The key to solving this puzzle is the concept of independence. Each monster is oblivious to what the others are doing. All we need to do is look at one monster, then apply what we've learned to the others.

Looking at one monster, he sees 10 targets. He, therefore, has a 1 in 10 chance of hitting the correct target (if he shoots at random). Conversely, there are 9 chances in 10 that he will miss. Your chance (probability) of surviving one laser wielding monster is 9/10.

When there are two monsters firing, you first have to avoid the first monster (9/10) and the second monster (who also has a 9/10 of missing). Mathematically, to and probabilities, we multiply them. So the chances of two monsters missing is 9/10 × 9/10. (The first monster misses and the second monster misses).

For two monsters, this can be written (9/10)². For three monsters, it is (9/10)³ … For n monsters it is (9/10)ⁿ

With ten monsters, the probability of surviving is (9/10)¹⁰ = 0.3487

The chance of surviving is approx 34.87% (better than 1 in 3)

This result might have surprised some of you as you may have imagined the chance of escape was very small with a similar number of monsters and targets.

It could be better, it could be worse

One in three is not bad (considering the alternative is certain death). How does the probability change if there were a different number of monsters? How about if your device could generate more holographic images?

The general equation that shows the probability of survival is show below.

Where N is the total number of targets, and m is the number of monsters.

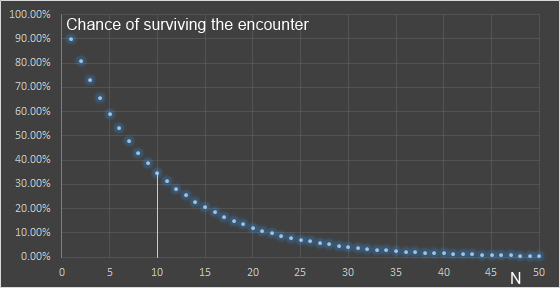
Changing the number of monsters (m)

Monsters	Survival
1	90.00%
2	81.00%
3	72.90%
4	65.61%
5	59.05%
6	53.14%
7	47.83%
8	43.05%
9	38.74%
10	34.87%
20	12.16%
30	4.24%
40	1.48%
50	0.52%
60	0.18%
70	0.06%
80	0.02%

If we keep the number of targets fixed at 10 (N=10) and vary the number of monsters m, we can see the effect on the probability of surviving from the table on the left.

Even at 21 monsters, there is a >10% of surviving an encounter if there are 10 targets. Also, if it were possible to reduce the number of monsters chasing you from ten to six, you would have higher than 50:50 chance of surviving!

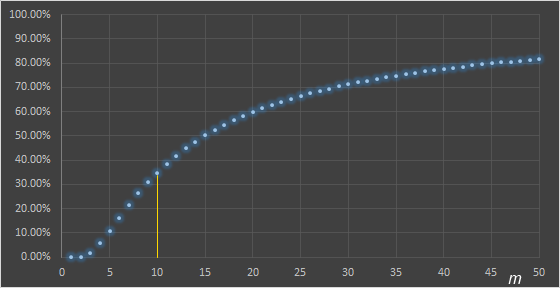
Changing the number of targets (N)

Targets	Survival
1	0.00%
2	0.10%
3	1.73%
4	5.63%
5	10.74%
6	16.15%
7	21.41%
8	26.31%
9	30.79%
10	34.87%
11	38.55%
12	41.89%
13	44.91%
14	47.66%
15	50.16%
16	52.45%
17	54.54%
18	56.46%
19	58.24%
20	59.87%
25	66.48%
50	81.71%
100	90.44%
500	98.02%
1,000	99.00%
10,000	99.90%

If the number of targets visible to the monsters changes (whilst still keeping number of monsters fixed at 10), the survivability percentages change to these values.

Obviously, if there is just one target (you, and no holographic twin), there is no chance of surviving the encounter.

With two targets, it's a coin flip if a monster shoots you or the dummy, so the chance for N=2 is like flipping a coin ten times in a row and getting heads each time <0.1% (not great odds)

Even with a hundred decoys, there is a 10% of not surviving.

With our starting conditions, given a choice of less monsters, or a device that can make more holographic decoys, it's better to elect for fewer monsters!

Equally matched (N=m)

What happens if we keep the number of monsters and targets the same, but adjust the number of them?

Something interesting happens. As the numbers increase, so does the survival chance, but it quickly asymptotes to 36.79% percentage chance. This is an important ratio.

N,m	Survival
1	0.00%
2	25.00%
3	29.63%
4	31.64%
5	32.77%
6	33.49%
7	33.99%
8	34.36%
9	34.64%
10	34.87%
20	35.85%
50	36.42%
100	36.60%
1,000	36.77%
10,000	36.79%
100,000	36.79%

With just two monsters and two targets, you have a 25% chance of surviving (this is easy to see; both monsters have a 1 in 2 chance of hitting the only decoy so it is ½ × ½ = ¼). With three monsters and three targets it is ⅔ × ⅔ × ⅔ …

Mathematicians call events that have two outcomes Bernoulli Trials. The mathematical explanation for the 36.79% limit can be shown be taking the limit as the number of monsters and targets tends to infinity:

The 1/e ratio occurs in many surprising places in mathematics. For example, it can help you decide How to select the best spouse (or secretary).

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.