Clover leaf problem
Here's another little geometry puzzle. Below is a square with sides of length 'a'. Inscribed are four semi-circles, each also with a diameter of 'a' units. The overlapping circles make a clover-leaf pattern. What is the area of this clover leaf? (shown in blue below).
 |
What is the area of the blue clover-leaf design? |
It's not a hard problem, so let's look a couple of different ways to solve:
Geometric Solution
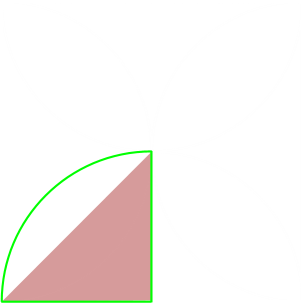 |
Looking at a corner we can can see that half a petal and a triangle make up a quarter circle.
If we subtract the triangle from a quarter circle then we can find the area of half a petal. There are eight half petals in the clover leaf. |
All we need to do is multiply the half petal by eight to get the area of the clover. Interestingly, the eight triangles have the area of the square, which is a2. Below we can see the equation for the result (It's always a fixed ratio of the area of the square).

Set Theory
An alternative way to solve this problem is with boolean mathematics and something called the Poincaré formula (named after French mathematician Henri Poincaré), which relates to the relationship between overlapping sets. It's also called the inclusion-exclusion principle.
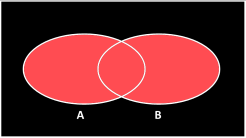
Imagine we have two sets, A and B. Items can be in neither set, one set, or both sets.
 |
 |
 |
Mathematicians use special symbols to donate operations between sets. One is the union, which is given the symbol ∪ and is the computer science equivalent of saying 'or'. It's what you get if you combine the two regions either side of the operator. The result of the operation is a set of items that are in either set.
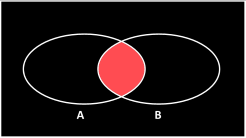
Another is the intersection, which is given the symbol ∩ and this is the computer science equivalent of saying 'and'. It's the overlap between the two sets on either side of the operator. The result is the set of items that are in both sets.
There is a relationship between the sets and their properties:

What this means is that you can find the items that are in either set by adding the sets together then subtracting the items that are in both (so that they are not double counted).
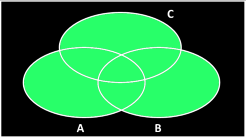
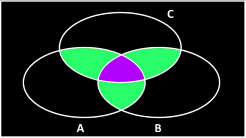
Expanding this idea, we can deal with three overlapping sets. It gets a little more complicated because we have interactions between different sets. Items can be in none, any one of the sets, a combination of two, or all three.
 |
 |
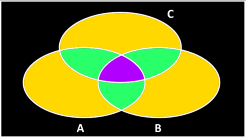 |
There is a similar inclusion-exclusion equation for three overlapping sets:
(Combine all the items, then subtract away the ones that you counted twice in the overlaping regions between two sets, then you need to add back in the region common to all three because that got taken out too many times in the subtraction).
Four regions
We can continue with this inclusion-exclusion for more and more overlapping sets (but after three sets it becomes much harder to visualize on 2D Venn diagrams). For our clover-leaf puzzle, however, not every set overlaps every other set. We have four semi-circles. I'm going to use the letters T, B, L and R to represent the Areas of the four shapes: Top, Bottom, Left and Right.
 |
 |
 |
 |
| Left | Top | Right | Bottom |
We can describe an equation for the relationships between them:
This looks a little messy at first glance, with lots of cross-correlations, but interestingly, lots of things just fall away:
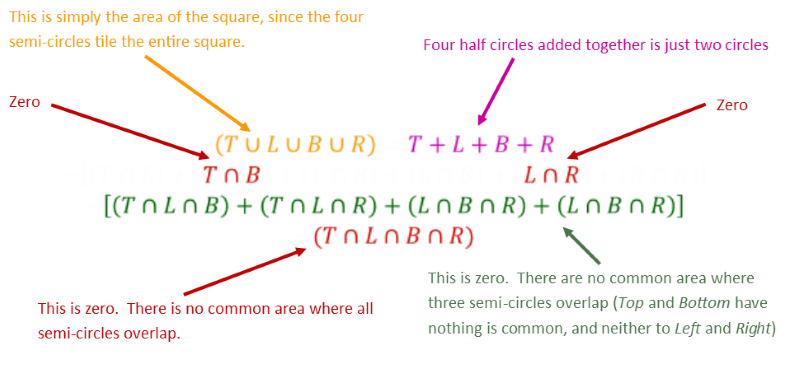
Removing all the terms that are zero (no common overlapping areas), the terms left in white in the above equation is the area of the clover leaf. Rearranging and computing the area of the circles and the square simplifies the equation right down.
We're left with the result that (thankfully) is the same as the result we obtained from geometry.
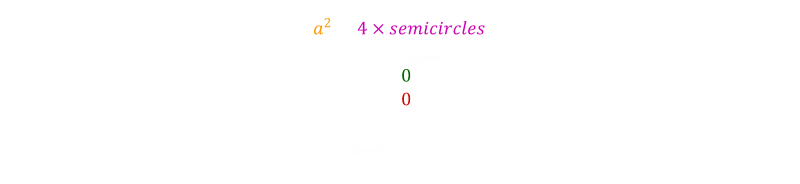
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.


