How far can you overhang blocks?
As a kid, I’m sure you played with stacking blocks. Maybe you still do. Here’s a question for you:
How far out is it possible to overhang blocks from the edge of a table without them toppling?

Rules, we need rules. All games must have rules. Here are ours:
Rules
|
 |
Obviously, as we build upwards, we can skew each level slightly to cause an overhang, but how far can we take this without it toppling over? Is it possible to build outwards from the edge of the table farther than the length of one of the bricks? If so, how much further?
Is it better to make big skews (displacements) at the bottom of the tower and smaller at the top, or uniform skew all the way up the tower, or small displacements at the bottom and large at the top?
This is a classic physics puzzle and is sometimes given the name “The Leaning Tower of Lire”
The Leaning Tower of Lire
|
I’ll give the startling answer first, and then proceed onto the proof. Yes, it is possible to build a tower that extends farther out from the edge of the table than the length of a block! This is one of those puzzles that, unless you’ve heard the solution before, defies belief. Logically, how can it be possibly to balance a block extending into the void beyond the edge of the table, and thus, be suspended in the air with no part of the top block overlapping the base block of the tower? Let's find out … Yertle The Turtle would be very proud! |
 |
Proof
 |
Before that incredulous expression of disbelief evaporates from your face let’s walk through the physics. It’s all about the concept of Center of Mass. |
Let’s define all our blocks to be of length one unit, and of mass M.
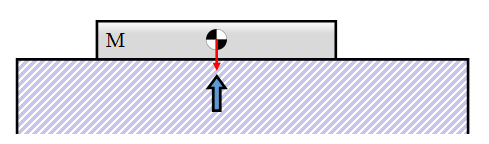
With a single block resting on a flat surface, it’s weight force acts downwards. In accordance with Newton’s Third Law, this force is reacted by the table. (We can represent the weight of the brick by a single force passing through the center of mass of the brick).
These two forces balance one another with no offset, so there is no torque, or moment, twisting the block. It is stable. It’s possible to slide the block towards the edge of the table, and providing the center of mass remains over the table, then the block is stable.
If the center of mass moves beyond the edge of the table there is no way its weight can be reacted without a moment and the block will topple off the end. Game Over!

We now have our solution for a one block tower! We can slide the block half way over the edge.
|
This result is very important. It gives us the deviation of the top brick of the tower. In this case it's a trivial solution, because our tower is currently only one brick tall, but imagine that the table it is resting on is the rest of the tower beneath it. |
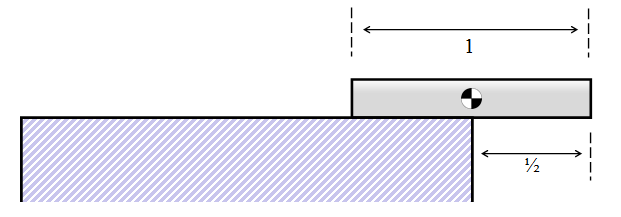 |
Whatever the make-up of the tower below, if it is stable, we can always place the top brick so that it extends half way into the void.
A tower is just stable when the center of mass of its structure is directly above the edge of the table.
Two Bricks
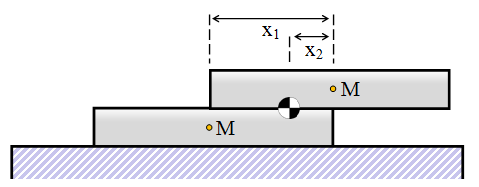
Now that we know the solution for one brick, let’s make our tower a little taller by adding another layer. The resulting stack will look something like this:
 |
As before, what we need to do is calculate the center of mass of the structure.
There are two bricks, each of mass M The distance between the combined centre of mass of the tower and the right hand edge of the bottom brick we'll define as X2 The distance between the centre of mass of the lower brick and right hand edge of the bottom brick we'll define as X1 |
Providing the combined center of mass of the structure remains over the table, we know the tower will be stable (and we already know that the top block is stable up until half way out).
Resolving moments around the right hand edge of the lower block, we get:
X2.(2M) = X1.M
(The moment of the combined center of mass of the entire tower around the lower right corner is equal the sum of the moments of the individual bricks. Since the moment of the top brick passes directly through this chosen origin, it is zero).
We know that X1 = 1/2, so this gives us the result that X2 = 1/4
|
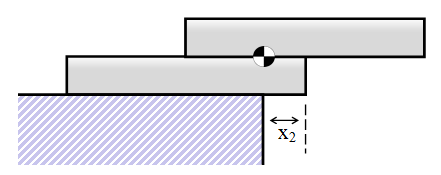
This gives us our second result. We can slide the combined block tower until the center of mass of it is directly over the edge. This will occur when we move it a distance X2 We can slide the lower block until 1/4 of it overhangs the edge. This will place the combined cener of mass directly over the edge of the table. At this point, the overhang is 1/2 + 1/4 = 3/4 of a brick. |
 |
Three Bricks
Now we're getting going … let's add another brick under these two. (As above, we know that the 1/2 + 1/4 configuration is stable, so we can place this two brick construct ontop of the third brick, instead of the table).
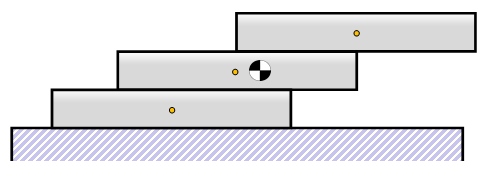 |
Again we're looking to calculate the center of mass. This time there are three bricks, each of mass M |
An alternate way to think of this is to coalesce the previous two brick solution into a single entity and place this on top of the third brick.
|
The distance between the combined centre of mass of the tower and the right hand edge of the lowest brick we'll define as X3 Resvolving moments around the lower right edge again (again, useful to do it from this origin as the moment from the force of the bricks above it is zero) we get: X3.(3M) = X1.M |
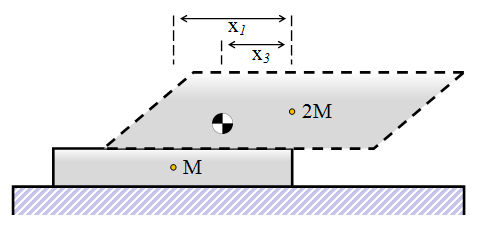 |
We know that X1 = 1/2, so this gives us the result that X3 = 1/6
As before, we are now able to slide the combined tower until the lowest block overhangs the edge of the table by 1/6
The combined overhang is now 1/2 + 1/4 + 1/6 = 11/12. This is close to one complete unit of overhang, but we're not quite there yet.
Let's keep going …
Four Bricks
We're getting the hang of this now! (See what I did there?)
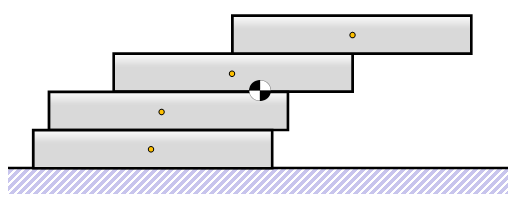
We need to calculate the new center of mass …

Resvolving moments around the lower right edge:
X4.(4M) = X1.M
We know that X1 = 1/2, so this gives us the result that X4 = 1/8
The combined overhang is now 1/2 + 1/4 + 1/6 + 1/8 = 25/24. This is greater than one!
By the time we've placed our fourth block, if we're careful, we can balance it so that no part of it lays above the edge of the table! This is awesome!

Generic Solution
I think you should be able to spot a pattern now. Here is a diagram for placing block n
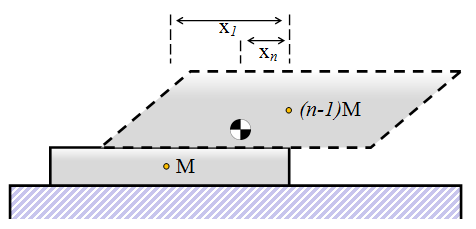
The displacement for this block is given by the equation:
Xn.(nM) = X1.M
|
So on each level, the optimal displacement for each block is 1/2n To calculate the total overhang, we need to sum the displacement at each level: Overhang = 1/2 + 1/4 + 1/6 + 1/8 + 1/10 + 1/12 + … + 1/2n
Mathematicians will recognize this as a Harmonic Series. |
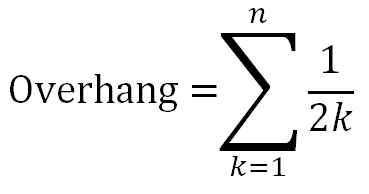
|
Results
Here are results for the first dozen rows of blocks:
|
 |
As you can see, the solution diverges (albeit slowly). As calculated above, the overhang exceeds 1 after four bricks.
As we will see later, to get to an overhang exceeding 2, we need 31 blocks, and to exceed 3 we need 227 blocks.
If we were able to balance 100,000 blocks ontop of each other, the overhang would be just of 6.045 units.
Harmonic Series
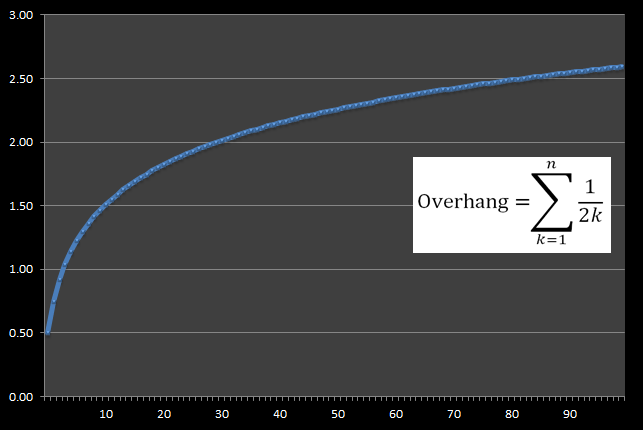
The first thing to notice is that this series is divergent. With each new level, the overhang possible increases. This gives the surprising conclusion that, theoretically, we can span any distance if we build our tower tall enough. There is no limit to how much we can overhang!
Let's investigate more about the infinite Harmonic Series, as shown below

In mathematics, Harmonic Series sums occur so often, they are given their own symbol: H(n) to represent the sum of the first n terms of the series.
The total overhang can be represented as 1/2.H(n) (as the total overhang is represented by the sum of 1/2n, not 1/n)
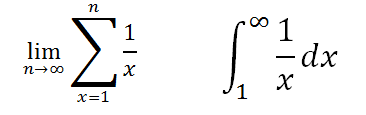 |
Those who have studied calculus may see the similarity between the term on the left, our Harmonic Series sum, and the standard integral on the right. At the limit, as we tend to infinity, the results merge. |
You may recall from Calculus that the standard integral of 1/x is ln(x), and the integral represents the area under the curve. The diagram below shows how the approximation is represented. The logarithmic approximation under-counts the true summation of the rectangles by the regions shaded in orange.
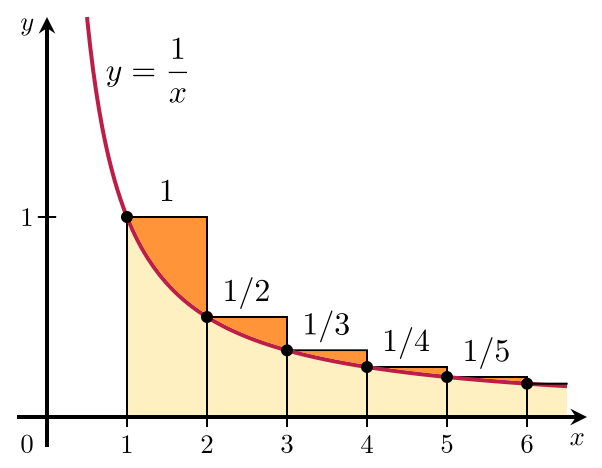
The summation of these orange regions is given a name, it is called the Euler-Mascheroni constant and is typically represented by the symbol γ
Whilst not currently proved, it is assumed that this constant (like Pi and e) is irrational.
The formal definition of the constant is shown on the right. It is defined as the limiting difference between the harmonic series and the natural logarithm. γ = 0.5772156649015328606065120900824 … |
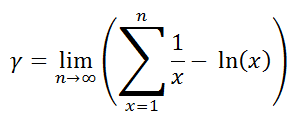 |
Armed with this information, we are able to approximate solutions to the block stacking problem without having to calculate long series of summations. Here are a selection of results:
| Desired Overhang | Layers needed |
|---|---|
| 2 | 31 |
| 3 | 227 |
| 4 | 1,674 |
| 5 | 12,367 |
| 6 | 91,381 |
| 7 | 675,214 |
| 8 | 4,989,192 |
| 9 | 36,865,413 |
| 10 | 272,400,601 |
| 15 | 6,000,022,499,694 |
| 100 | 4.057e+86 |
| 200 | 2.932e+173 |
| 300 | 2.118e+260 |
Big Numbers
These numbers are incomprehensible.

|
Let's work with something easier to handle, a deck of cards. A standard deck of cards contains 52 cards, and is approximately 2 cm thick. |
|
With no wind, a lot of time, and a ridiculous amount of patience, it’s possible to make a tower like the one on the right. (Vertical axis not to scale). The overhang for 52 cards is approximately 2.269 times the width of one card. Not bad. Let's say your best friend's dad runs a playing card factory and you have access to millions of packs of playing cards, if you built a tower of cards as tall as the Empire State Building how much overhang could you get? |

|
 |
The Empire State Building is 443.2m tall (that's 1,454 feet for my Metric challenged readers), that's about 22,160 packs of playing cards (thank you best friend's dad), which would create a stack of cards 1.152 million cards tall. Using our forumla we can calculate the overhang, and it's 7.267 units. Not bad, but I'd worry about the compression loads at the bottom of the pile! Let's say we wanted to double this overhang distance to 14.5 units. How many cards would this take? The staggering answer is 42 billion decks of cards. A stack of cards this big would be 849 million meters tall. That's more than twice the distance from the Earth to the Moon (and Space is a really, really big) 
|
Go and Try
OK, now that you know the theory, go out and try it yourself! How hungover can you get?
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.

