Combining Estimates
 |
I have many skills in life, but judging the age of people is not one of them! Let’s pretend that you know, from past experience, that I make age estimation errors that are normally distributed and have a standard deviation of 5.5 years. A colleague at work has much better age estimating skills. Let’s say that, based on her historic performance, her standard deviation is a more respectable 2.3 years. |
|
A person, who neither of us has met before, appears. I estimate the age of this mystery person to be 54 years old. My colleague estimates her age to be 64. Is it possible to combine our two (independent) estimates to get a more accurate prediction, and if so, what would be this estimate? It might be tempting to just accept my colleague’s estimates, since she has a lower standard deviation, but there is information gained from my answer too. |
 Image: Nell Moralee Image: Nell Moralee |
Blended Estimate
Let’s look at this generically. Let G1 and G2 be our respective guesses and σ1 and σ2 be our standard deviations.
We’re looking to create a blended estimate that will be combine some of my answer (and variance), and some of my colleagues. Let’s assume we do this with a linear weighting. We’ll take k of my estimate, and (1-k) of my colleague’s.
The Variance (the average of the squared differences from the mean) of our blended answers is added (because our estimates are independent). Variance is the square of standard deviation.
Differentiating the Variance with respect to k, and setting this to zero will find the turning points, and confirming that the second derivative is always positive shows that this corresponds to a minimum value for the Variance.
Rearranging this gives the value for k that gives the lowest Variance.
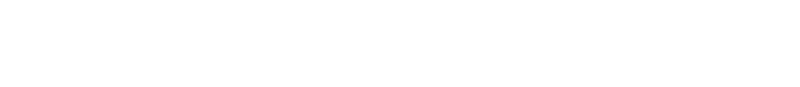
Substituting this back into our guess formula reveals the blended guess with the minimum Variance.
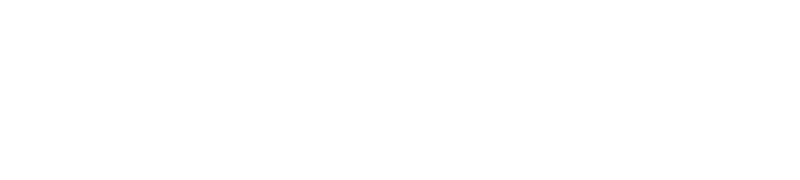
Answer
Applying the values of G1 = 54 and σ1 = 5.5, and of G2 = 64 and σ2 = 2.3, we get a blended estimate of ≈ 62.5 years old.
Related Articles
|
A little while ago, I wrote about estimating the number of people running in a marathon, and another famous similar problem is the application, during the Second World War, of estimating the number of German tanks procuced by examing the serial numbers of captured and destroyed tanks (also in that link). Here's an intersting sampling problem about how to estimate the number of unseen errors in a document after it has been reviewed by two independent people. |

|
Other interesting sampling problems
Here are some other articles that also consider sampling and imperfect views on collections to make estimates:
The Sectrary Puzzle (also sometimes called the interview puzzle, or the wife, or husband finding puzzle), deals with how to give the best chance of selecting the best person for a role when you are only allowed to see each person once. You interview a candidate once then have to give a hire/no-hire call and if you pass, you are never allowed to go back. At the start you have no idea of the spectrum of candidate qualifications, so you want to see a 'pool' of people first to judge the range. The larger the pool you consider before setting your threshold the better your accuracy, but then you are reducing the people you'll get to select from. Conversely, a smaller sample pool might give you enough of an accurate sample of the candidates. What is the optimal? …
Simpson's Paradox deals with the interesting way that answers can be inverted when comparing samples with different denominators.
By adjusting boundaries around which sampling can occur you can influence results. This is called Gerrymandering.
With imperfect information, what is the optimal strategy for playing the game Deal-or-NoDeal?
There is a danger that if you stop too soon in looking for errors you might get the wrong inpression of the average number of errors in the entire document. Maybe there is a higher concentration of errors in the first part of the document? If you visit a sports game, and a good percentage of the points are scored in the first part of the game, it might bias your opinion of the overall game. Here is an article which talks about, if you eventually win a game, what is the percentage chance you were winning the entire game (Bertrand's Ballot).
Here's a short primer on confidence levels and the central limit theorem.
What is the difference between Risk and uncertainty?
Finally, why there is no such thing as the Conservation of Luck.
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.

