Ring, ring! … answer the phone!
A little thought experiment today: Imagine there are three telephones, each mounted on a wall. Your job is to answer these telephones. The telephones are not symmetrically placed on the wall, and there is an equal (random) chance of any of the phones ringing. To answer a phone, you need to walk to it and pick it up.

The question is: Where is the best place to sit in order to minimize the average distance you need to travel to perform your duties?
(For the sake of our initial analysis, we’re going to assume that you also stand against the wall so the distance measured is simply that along the wall. We’ll examine what happens if we remove this restriction later).
Where to stand?

|
Should you stand at one end? That’s great if the phone you are standing next to rings (one chance in three), but for the other two times you have to walk, and one of these walks is the entire length of the room. Even if you chose to stand at end closest to the middle phone, one chance in three you’d have to walk a long distance. Clearly if you were going to stand at one end, there is a better end to stand, but it’s not the optimal answer. |

|
How about the middle? This will stop you having to travel from one end to the other, but whatever phone rings you’ll have to travel; you will walk on every ring. This solution would be the correct answer if you wanted to minimize your maximum regret. Standing in the middle is the answer if you want a solution that reduces your chances of walking the longest distance. |
|
The smarter people might answer “You should stand in the mean position”, and a first glance that seems like it might result in the optimal strategy, but actually, it doesn't. As we will see later, standing in the mean position is the place that minimizes the squared distance that you have to travel on average (least squares fit). |

|
The optimal strategy, in fact, is to stand in the median position, and since there are just three phones this time, this necessitates standing in front of the middle phone. |
|
You can convince yourself this is the optimal strategy with this thought experiment: Imagine you are standing directly in front of the middle phone. If you take one step to the left, you are reducing your distance to the phone on the left, but, you have increased the distance you have to travel to the two phones to your right. Similarly, if you take one step to the right, you are reducing the distance to the phone on the right end by one step, but you are increasing the distance you have to travel to the two phones on your left by one step each. |
 |
Whichever direction you move away from the median position, you are increasing the distance you need to travel. Opposite the middle phone is the global minimum.
Graphs
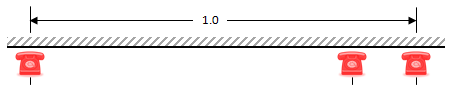 |
Need convincing? Let's fire up Excel and write a couple of formulas. For the rest of this analysis we’re going to normalize things by representing the distance between the two furthest phones as 1.0 |
|
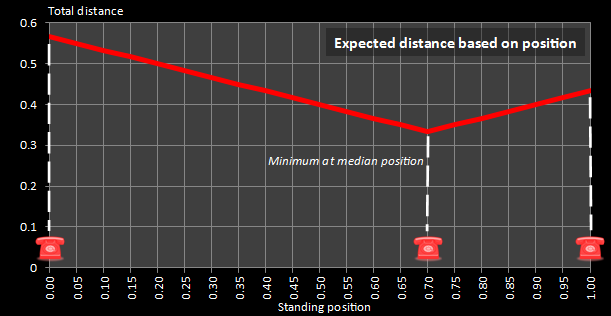
In the graph on the right I’ve show the average distance to travel for all positions between the two end phones. In this example, I’ve placed the middle phone at position 0.7 In this chart you can clearly see the minimum distance occurs when you stand directly over the middle phone. This is the median position. |
|
|
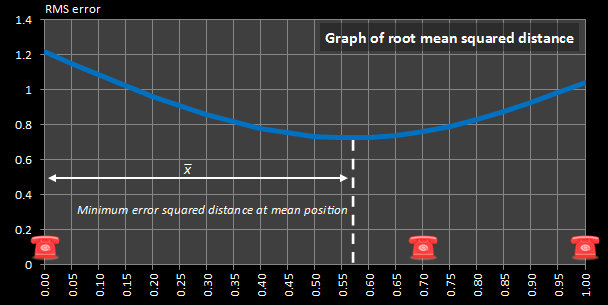
Remember back to discussion about the mean position? To the left is a graph of the average sqr (sum of squares) of the distance traveled. In our example, the mean is (0.0 + 0.7 + 1.0) / 3 which equates to 0.567, and you can see on the graph to the left this corresponds to the minimum in the function. |
More than three?
If there are more than three phones, the solution still stands. To minimize the distance one would need to travel to answer phones that ring at random one should stand in the median position. With an odd number of phones, that is easy, you should always stand opposite the middle phone.
|
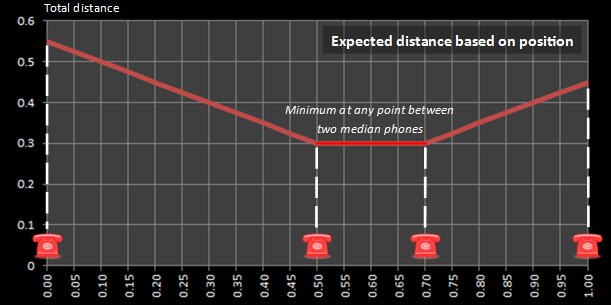
With an even number of phones, it gets a little more interesting. With an even number of phones, the median position lies between two phones. In this case, it really does not matter where you stand, as long as you stand somewhere between the two phones either side of the median. You can see this illustrated in the graph to the left which shows a solution with four telephones. A similar situation occurs with six phones, eight phones … |
What if we stand further away from the wall?
|
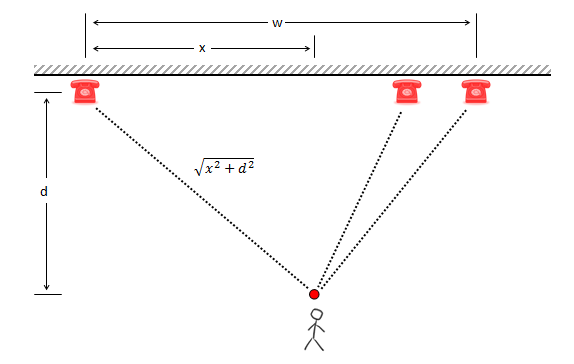
If you are not standing directly on the wall, your distance to each phone is modified by this fact. Assuming that you walk directly to each phone as it rings, we can use Pythagoras to calculate the true length of your path. When a person is directly against the wall, as we know, the optimal horizontal position is the median position. In this position, a person does not need to move to answer the middle phone. As the person moves away from the wall, they need to move whichever phone rings (There is no place to stand that is directly adjacent to a phone). This causes an interesting effect; it gradually moves the optimal (horizontal) position from the median position to the middle position as the person moves further away. |
|
(The mathematicians in the audience will see that, as the distance d increases, it dominates the equation determining the lengths of the path travelled. The difference between the lengths of the three paths gets smaller as d increases, and the optimal position to stand moves towards the mid-point).
Below, I’ve plotted curves for a variety of positions standing away from the wall.
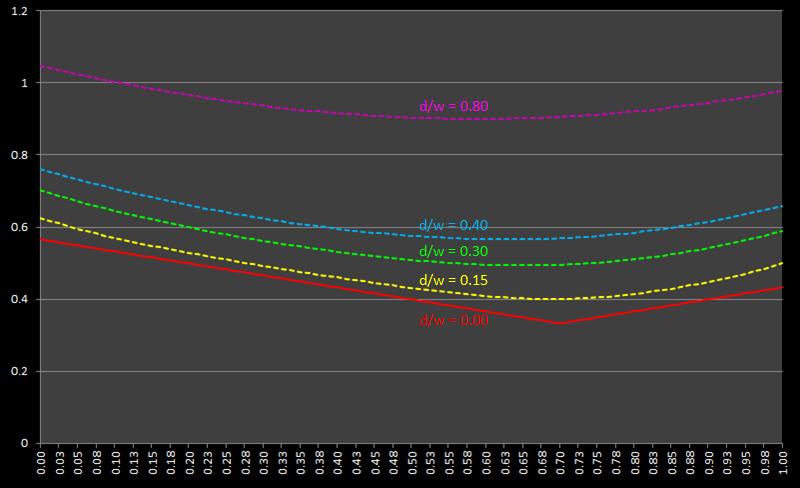
As the ratio of d/w increases two things happen: The first is that the minimum position migrates away from the median position and moves towards the center. The second is that the curve “flattens” (there is less difference between the longest and shortest possible distance that can be traveled).
Another example of the phenomenon
Let’s move from one dimension to two. Let’s imagine your job is to plan a conference for hundreds of attendees from around country. Your aim is to minimize the total distance that attendees will have to travel to visit your conference. If over half your attendees live in Seattle, it’s possible to show that in order to minimize the total distance, you should host conference directly in Seattle! (which is counterintuitive to a first blush common sense guess, which might have you selecting some common centroid point, which, as we now know, would result in the least-squares solution).
With over half the attendees in one location, you can see how the median must fall in that location, and thus we should host it there!
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.

