
	Advertisement

Golf Balls

Today I’m going to take a whimsical look at golf balls. There is no particular reason for this; It’s just a random excuse to dig out a little math.

Golf balls are not smooth spheres; they are covered by a series of dimples. This is for aerodynamic reasons. The dimples encourage the air moving over the ball to transition from laminar boundary layer to turbulent flow a little sooner. A turbulent boundary layer provides a way for more energetic* fluid to get mixed in closer to the surface of the ball. This encourages the air to stay closer longer and delays the flow separating in the adverse pressure gradient downstream of the widest part of the ball.

This, in-turn, makes the apparent cross-section of the ball smaller and because it ‘punches’ a smaller hole in the air as it travels (compared to a smooth ball), it has a lower drag coefficient and consequently travels further through the air than a smoother ball would (when hit with the same force).

A golf ball with dimples can travel about twice as far as a smooth ball. A golf ball is probably the best known shaped sport ball in in the World.

*Strictly speaking it has the same energy, it’s just air moving with more local velocity.

Size

Depending on which side of the Atlantic you live (there is a difference between an American ball and a British ball), the diameter of a golf ball is between 41.1mm and 42.6mm.

There are no regulations about how many dimples a golf ball has to have. Different manufacturers have different designs, and patterns between 300 and 500 dimples are common (with a popular design having 392 dimples). The design of these dimples also varies. On some designs they are uniform in diameter and depth, and in others there is a variation of sizes. Sometimes the dimples are spherical in nature, other times they can be truncated conical. I’ve also heard of designs that are hexagonal in shape.

Surface Area and Volume

Here’s question for you: How much does the addition of the dimples affect the surface area and volume of the ball?

The volume and surface area of spheres are given by the formulas below:

The dimples will reduce the volume of the sphere (they all press in). The surface area will could decrease, stay the same, or increase, depending on the geometry of the depressions.

Dimple Depth

If you imagine that a golf ball were a hollow thin shell, like an egg, and you drew a circle on the surface of the egg, cut it out, flipped it over, and glued it back, you'd end up with an object that is almost a sphere, but with a little dent in it. The volume be smaller, but the surface area would be exactly the same.

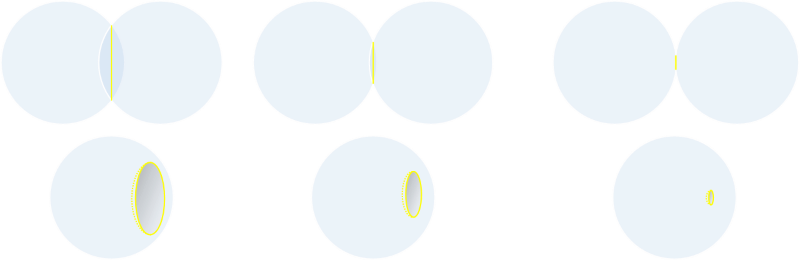
The dimples, however, would be very, very, shallow. The radius of curvature of the dimple would be large (the same as the ball), and considering the diameter of the dimples is very small, they would be very shallow.

We know, from inspection, that the dimples in a golf ball as much deeper. This means that the radius of the scooped out volumes (assuming they are spherical caps), is much smaller. This will mean they have a higher surface area than the cap they are replacing. The more dimples, the higher the surface area of the ball.

All this talk about carving out parts of smaller spheres from larger ones. Does that remind you of anything? (That's not a golf ball, it's a space station)

A little data

Let's perform our calculations by assuming a generic ball with diameter of 42mm, containing 400 dimples.

Research shows that dimples have a diameter of approximately 3.9mm, and have depth of 0.15mm

Without dimples, a smooth golf ball has a volume of 38,792mm³ and a surface area of 5,542mm²

Back to School

We need formulas for the volumes and surface areas of spherical caps.

A quick look at the Internet (to refresh our memories), finds the follow formulae:

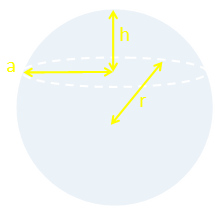An interesting thing about both of these equations is that neither of them require one to know the radius of the sphere. If you know the radius of the slice, and the depth of the cap, then the radius does not need to be calculated.

To calculate the volume of the golf ball, we need to start with a solid sphere, then subtract off the volume of 400 spherical caps to make a sphere with 400 flat areas, then subtract off again the volume of the dimple depressions.

To calculate the surface area, we start with a sphere, remove the area of the spherical caps, then add back in the area of the new (inverted) spherical caps.

The differences are very small. The volume reduction from a smooth sphere is approximately 1.48%. The increase in surface area from the dimples is 0.324%.

It's amazing to think that little differences like this can cause the ball to fly almost twice as far!

Trivia: World Records

What's the fastest anyone has ever driven a golf ball?

Canadian long drive champion Jason Zuback broke the world ball speed record on an episode of Sport Science by hitting a golf ball (with a golf club!) and launching it with a speed of 328 km/h (204 mph). That's faster than the top speed of my car!

The world record recognized by Guinness Records as the longest drive in a competition is 515 yards (471 m) by 64-year-old Mike Austin in 1974 at the US Senior National Open Qualifier with a 43.5" steel shafted persimmon wood driver … but is this the longest drive? …

In 1971, astronaut Alan Sheppard hit a couple of golf balls on the moon after landing there on Apollo 14. With pretty much no air resisitance, and significantly lower gravity, there is potential for them to have travelled a long, long, way. As it happens, it's estimated his best shot was about 200 yards (I'm guessing that a space suit really restricts a swing, and he swung single handed!). But there is one other non-earthly contender …

Russian cosmonaut, Mikhail Tyurin, hit a golf ball whilst he was tethered to the International Space Station. The ball left the station from 220 miles in orbit over the Pacific Ocean. By the time it had decayed enough to be destroyed by the atmosphere in re-entry, it would probably have travelled around a couple of million miles. (It's probably not eligable for a record, however, as a non-standard ball was used. In an effort to mimimize damage to anything, should it have hit something, the mass of the ball was about 1/15th of a regulation ball).

And remember, never play golf with OddJob!

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.