Distributing passwords
Just about everything we touch online these days requires a password (and certainly all sensitive information is protected by one).
|
Passwords work because they are a secret. At its most basic, a password is a key, theoretically, only known by the person(s) who are supposed to know it. Knowledge of a password gives access to the person who is aware of the secret. Most password systems only use one password and only require one person present to unlock. Its analogous to a door with a lock. |
 |
 |
What if you wanted to add additional levels of security such that it required more than one personís permission to access some service? (More than one lock on the door). Here are a few examples:
However, with a little imagination we can conceive some more advanced scenarios: |
Advanced Scenarios
With your business partners, you agree that any two of the four people, together, have sufficient privilege to access the bank account. It can be any combination of two, and at any time it might be a different pair.
To launch the nuclear missile, you define a hierarchy of passwords with different strengths. The password of The President, for instance, could count as three votes. That of The Secretary of Defense counts as two, and all others count as one. So, The President and The Secretary of Defense, together, have the authority to launch the missiles, as does The President and the votes of three ordinary grunts, or five grunts together … etc.
Maybe some of the family members who have passwords to read the will are old, and might die themselves before the will is to be opened. You donít want to encrypt the will and find out that, if some of the other members of the family pass on, that the information in the will is lost forever. You would also like the ability to grant passwords to newly discovered “next of kin” family members without requiring those already holding passwords to have to change theirs.
 |
Or how about a totally weird scenario (which is really just a canononical form of the examples above)?:
Someone is hopeless at remembering passwords, so elects to write their password down. However, they do not want their password to be written where anyone can simply read it, so they break it up into a set of twelve sub-passwords. These sub-passwords are then hidden. They put one in their wallet, another in their desk at work, one on a bulletin board in the kitchen, one in the bedside table, one on their laptop, one at their brotherís house … Any subset combination of four of these is required to gain access, and any less than this is totally useless. When access is required, the nearest four sub-passwords are retreived and correctly used.
Ideal characteristics

These are interesting challenges. Before I show a solution, itís worthwhile enumerating, explicitly, the desired characteristics of a good multi-password solution:
If a password is broken down into a collection of sub-passwords, exposure of one of the sub-passwords should not give an attacker any further hints of the solution. (For example if there are four passwords in a set and, for whatever reason, I know password P1, if I also learn the values of P2 and/or P3 or P4, it should give me no more knowledge about how to unlock the cypher than I have by knowing just P1). All sub-passwords should be required to obtain a solution, and knowledge of even all-but-one of them, should give the attacker no more advantage then knowing none at all.
Ideally, the sub-passwords in the set should by the same order of magnitude in length as the master password they combine to create. (We donít want to turn a 12 character master password into 6 sub-passwords that are hundreds of characters long each).
It would be desirable, if one of the sub-passwords happened to be exposed, to allow a new master password to be generated without having to re-issue new sub-passwords to the non-exposed ones (So you can give a password to your brother before he leaves on a 10 year off-the-grid expedition and be able to allow him keep the same password, even if things change). Bonus marks if he can keep the same password if the number of sub passwords changes through the years (additions or subtractions).
It would be nice to have the ability to generate new viable sub-passwords without having to re-issue all new passwords. (For instance, if one of the sub-passwords was written on piece of paper which got burned before anyone could read it).
There is a system for generating and decoding passwords that enables all of this functionality. Itís called Shamirís Algorithm. Weíll look at how it works in short while, but first letís look at some other solutions that partially work, and examine their limitations …
Password Carve-up
This is as simple as it sounds; we simply take the master password and carve it up into the number of sub-passwords we desire. For instance if the master password is ďPRINCESSĒ, we could distribute this to four people like this:
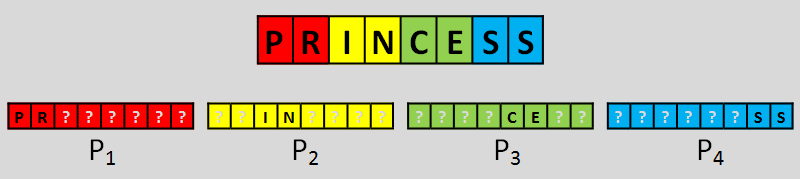
We donít have to do this at a character level, we could perform it at bit level if necessary, carving up a string, and/or we could stripe the slices rather than taking it in chunks, but however we do it, its not ideal.
It doesnít take too long to see issues with a carve-up strategy. The first issue, is that it gives away part of the final solution in the clear. Each password contains part of the master solution, greatly reducing the space that a brute-force attack would need. Secondly, if you happened to “stumble-upon” other sub-passwords, you could append these to yours and further reduce the address space. Each sub-password you encounter gives you more information about the solution.
|
Itís not a very elegant solution. Fundamentally, though, the biggest drawback is the need to have all components present to unlock. If you break a password into n sub-passwords, then you need all of these present to recreate the original! This does not fulfill our desire to be able to grant access to a smaller subset of people. It's like smashing a plate into lots of pieces. You need to have all the pieces if you need put it back together again. |
 |
Random Offsets
A slightly more elegant solution, which solves the problem of exposure of multiple passwords giving you more information, relies on the concept of random offsets. Whilst this solution is superior to the carve-up method, it still suffers from the restriction that all sub-secrets need to be present to be recombined to generate the original password. It's still a broken plate reconstruction problem!
Letís imagine that the secret we are trying to scramble (our password) is a number. We call this secret number S. (If our secret is not a number, itís very easy to encode a text string into a number).
If we want to generate n sub-passwords, all we do is generate n-1 random numbers (positive or negative).
Letís call these random numbers: R1, R2, R3 … Rn-1
For the last sub-password, we give it the value: (S - R1 - R2 - R3 … Rn-1)
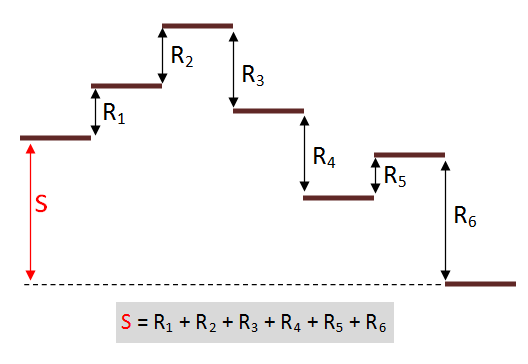 |
To the left is an example of breaking the password into six sub-passwords. The first five sub-passwords are randomly generated, and the last is calculated such that adding all the sub-passwords generates the required sum. Now, to recreate the secret, everyone simply needs to add their sub-passwords. Individually, nobody has any information about what is the secret and what is random, and even if n-1 people got together and colluded, they are still unable to determine from the missing piece what is random and what is real. |
Exclusive Or
Another variant of this uses the bitwise exclusive or operation XOR. (One or the other, but not both).
 |
The XOR function has a useful property that when applied twice with the same value it returns the input to its original state (A XOR B) XOR B = A As before, the first n-1 sub-passwords are created as random numbers. To generate the last we calculate it using the formula S XOR R1 XOR R2 XOR R3 XOR … XOR Rn-1 |
To reveal the secret S we get everyone to XOR their sub-passwords. The double application of XOR on each random number toggles each bit to its original state.
As before, this system will only work if all sub-passwords are present, which is both a blessing and a curse. Without all sub-passwords being available, collusion or exposure of any combination of passwords will reveal nothing about the solution.
Shamirís Algorithm
|
OK, itís now time to reveal an algorithm that meets all our requirements. The algorithm I'm going to discusss is called Shamirís Algorithm. It involves a little math, but not too much, and Iíll try to introduce the concepts slowly. Key to the utility of this algorithm is that it does not force the restriction that the number of sub-passwords to decrypt has to be the same as the number of sub-passwords generated. We can tweak the parameters such that any number of sub-passwords (less than or equal to the total number generated), can be used to unlock. All the King's Horses and all the King's men, would be proud! It is possible to put Humpty Dumpty back together again … and we don't need all his pieces to do it! |
 |
Back to school
|
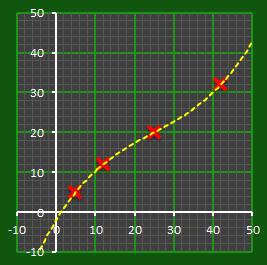
Imagine a sheet of graph paper. On this piece of graph paper weíre going to plot a point. For this example, we'll use the coordinates (25,20) This is your password! (bear with me, all will be revealed later). If I asked you to draw a line that passed through this point, how would you draw it? |
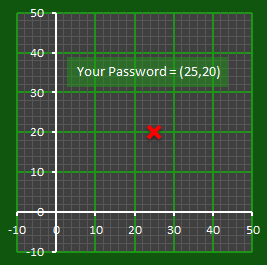 |
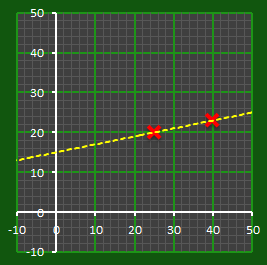
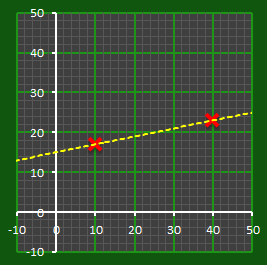
Below are some example lines. In fact, there are an infinite number of ways to draw a line through one point. To correctly desribe a straight line using points, you need at least two.
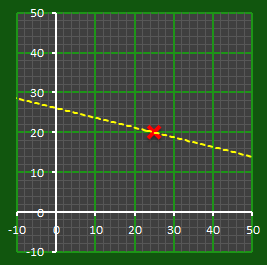 |
 |
 |
This is where we introduce our secret S, by setting this as the intercept with the y-axis. There is only one line that passes through this intercept and also through our coordinate (see below).
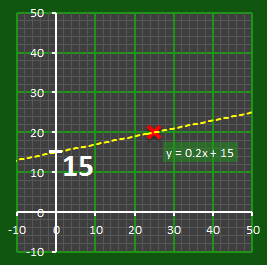 |
The equation of a straight line can be described with the equation: Y = mX + C Where m is the gradient (slope) of the line, and C is the intercept (where the line crosses the vertical axis). We can see that the secret S is the intercept (C) of a unique straight line that passes through our point. Only this line passes through these two points. |
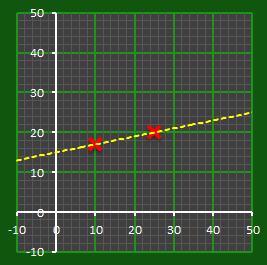
Any two points along this line are all that is needed to describe the line, and using these two points allows the intercept to be determined.
 |
 |
 |
And here, in its simplest form, is our algorithm. In this implementation, because it is a straight line, two points are needed.
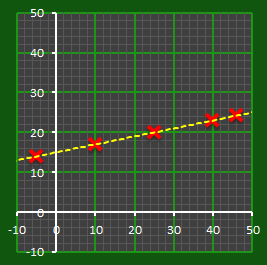 |
We can create any number of points on this line that we desire. We can distribute hundreds of coordinates and give them out. Individually, each coordinate is totally useless. There are an infinite number of potential lines that pass through any single point. However, if two people get together and pool their knowledge, they can recreate the line and thus determine the intercept, and find the secret. As you can see from the geometery, it can be any two people. Awesome! |
OK, let's move on from linear to quadratic. Straight lines are what mathematicians call order-1 polynomials. To describe a straight line, in addition to the constant C, you need just one parameter, which describes how to apply the independent variable. This is why you need two points to fully describe a line; you need to two simmultaneous equations to determine the parameters.
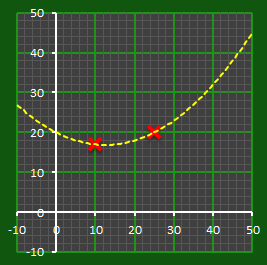
Quadratic equations are order-2 polynomials. To describe a quadratic, in addition to the constant C, you need two parameters.
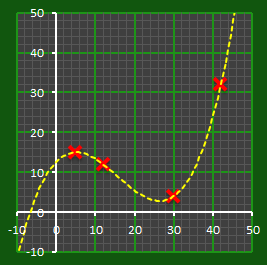
A quadratic equation can be described by the function y = Ax2 + Bx + C
With only two points, there are an infinite number of quadratic curves that can be fitted through them. Here are a few examples:
 |
 |
 |
I think you can probably see where we are going with this one. As before, we'll encode our secret S as the intercept of our polynomial with the y-axis. Now, all we need to do is describe the curve.
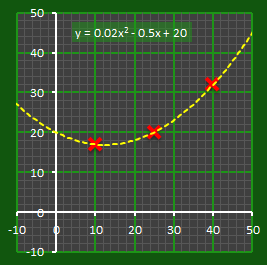 |
Here is an example quadratic curve. Using three points we can completely describe a quadratic curve. As with the linear example, we can create as many point as we desrire along the curve and give these sub-secrets to whoever we wish. With a quadratic, however, three of these people need to get together to decode the secret. It can be any three people, but three people are needed. |
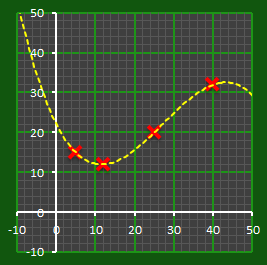
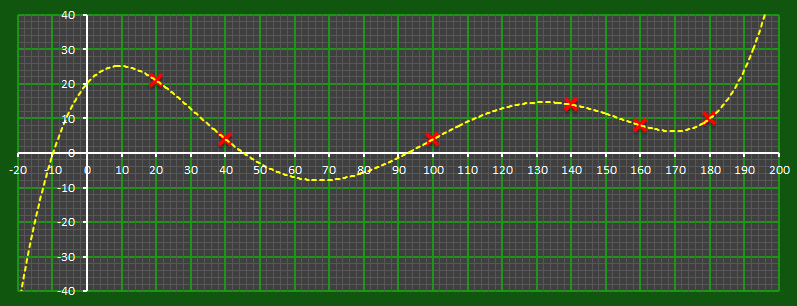
And so, on and so on. Here are some order-3 polynomials (commonly called a cubics). Four points are needed to fully describe a cubic function. If we encoded our secret with a cubic function and distributed coordinate sub-passwords it would require any combination of four points to determine the intercept and the secret.
 |
 |
 |
We can keep increasing the degree (order) of the polynomial as needed to break the problem down into the required number of slices. An order-n polynomial curve requires n+1 points to accurately describe it.
Advanced feature support
Let's review the list of ideal characteristics discussed above and see how this solution handles them:

|
We can see how this algorithm is not a broken-plate type problem. We don't need all the sub-passwords to re-create the secret. All we need is sufficient to mathematically solve the order of the equation we are using. |

|
Knowledge of any non-complete combination of sub-passwords gives an attacker no additional information on how to solve the problem. Even if you have knowledge of n-1 passwords, there are still an infinite number of curves that fit through these points, and thus an infinite number of possible intercepts. |

|
As we can clearly see, it's very easy to generate new sub-passwords as needed. If we need to generate and distribute a new sub-password, we simply pull off another coordinate from the curve and give that out! None of the existing passwords need to change. |

|
If some of the sub-passwords are compromised (and you know which ones) and you want to regenerate new ones, but keep the uncompromised ones the same, you can generate a new curve that passes through the points you wish to keep. [Edit - Only if the the number of uncompromised points is two (or more) less than the minimum number needed to reconstruct the secret. Thanks for the correction @N1DQ] |

|
To weight passwords (such as giving The President a nuclear launch password with three times the power of a regular password), we simply give out multiple coordinates to that person. Thus, for the nuclear launch example requiring requiring five votes, we generate an order-4 polynomial, give The President three coordinates from the curve, The Secretary of Defence two coordinates off the curve, and the rest of the troops one coordinate each. |
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.

