
	Advertisment

Smarter Filling

Today I was cleaning up some more files and came upon some code I wrote many years ago to solve a display problem.

The problem

Let's say you have a collection of data and wish to display this on a web page as a series of shaded rectangles.

You want the area of each rectangle to be proportional to the data, but in addition you also wish to tessellate these rectangles perfectly so that they fill completely the screen.

Here are some sample outputs from a test program I wrote:

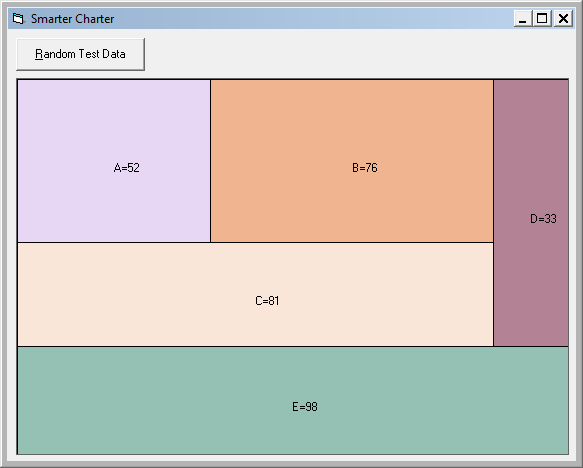
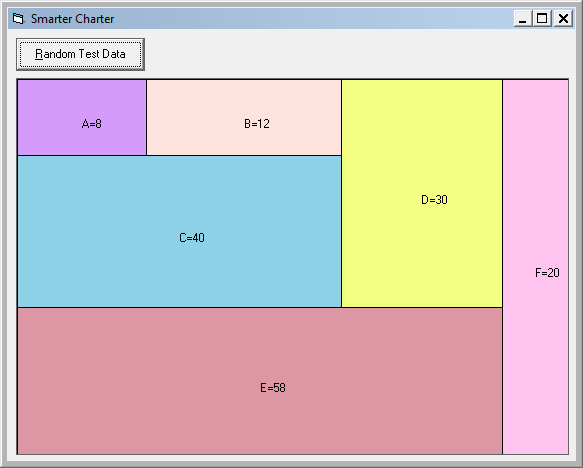
The algorithm starts off by placing the first element in the top left corner, then alternately attaching the next element either on the end, or the bottom of the current collection, adjusting the floating dimension to ensure the area of this new addition is correct.

Because of geometery, applying an arbitrary scale factor to either axis preserves the ratio the areas to each other, so it's trivial to stretch the current solution to allow the next element to be attached to the end.

It's not a particulary clever algorithm, and tends to make the the latter added elements very 'finger like', but it was very quick to write, and did the job well enough for this purpose. Like many problems in Operational Research, sometimes getting to a 98% optimal solution in a very short time, is far more useful than 'investing' dozens of hours in getting to a 99% solution.

Try asking a travelling salesman who has to visit a dozen stops in the most efficient order …

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.