
	Advertisement

Grazing in a circular field

I’ve written a little about grazing before (How to calculate the optimal dimensions for a rectangular field using just straight fences).

This week we’ll look at another classic grazing math problem. This involes a goat grazing in a circular field.

Old MacDonald, on his farm, has a large circular field. He also has a goat. He tethers the goat, using a rope, to a post on the circumference of the field. He wants the goat to be able to graze half of the grass in the field. Here’s the question: What length should he make the rope?

How long a rope will allow the goat to graze half the circular field?

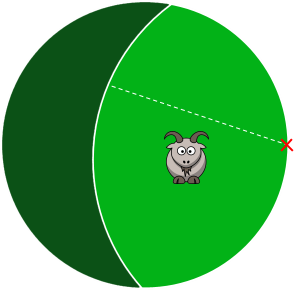This is a pretty old problem. The earliest published version of it is in 1748, in the yearly publication The Ladies Diary. (It's also spawned a whole class of other related puzzles in which the field contains a barn, or a silo, that the goat is either tethered to, or is restricted around because the rope wraps). Today, we'll just investigate the vanilla variant.

Problem

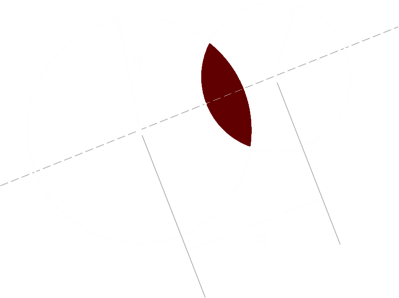
The rope constrains the goat into the lens shape bouded by two circular arcs; the lighter green in the diagram above. The complementry part of the field, that the goat cannot access, is give the name of a lune in reference to it's shape like the crescent of the Moon (The Latin word for 'Moon' is 'Luna').

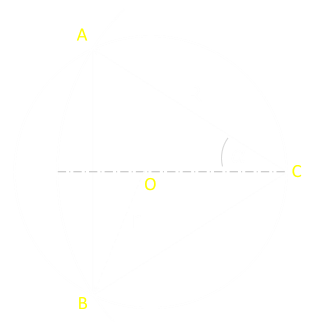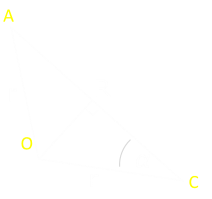
It's pretty easy to see that, for the goat to be able access half the field, the length of the rope needs to be longer than the radius of the field, but let's formulate a generic answer to the problem.

To the left is a diagram of the field.

We'll define the radius of the field to be r.
O is the center of the field.
C is the point on the circumference of the field where the rope is tied.
R is the length of the rope (and thus also the radius of a circle centered on the tether).
Points A and B are the intersections of the two circles.
Angle α is half the angle ACB.

Shapes

The area the goat can graze is the sum of the yellow sector, and two of the red segments.

If the angle α is in radians, then the area of yellow sector is: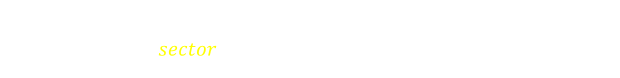

The area of the two red segments is:

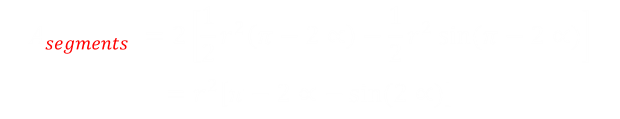
Combining these, and normalizing to set the field to be a unit circle r = 1

Let's clean up by substitution for α:

We can derieve expressions for for the angle, based on radii, using this triangle

And similarly normalizing with r = 1

Using the identity Sin(2x)=2 sin(x) cos(x), and substituting in, gives the answer:

This is not an amazingly pleasing or elegant answer; to be honest, I was expecting a cleaner answer, oh well. It is best solved numerically (using something like Newton-Raphson, or in my case, the Goal-Seek function in Excel!)

Here is a graph of the equation. On the x-axis is plotted the length of the Rope (R), as a ratio of radius of the field. On the y-axis is the ratio of the percentage of the field covered. You can see that as the length of the rope increases to twice the radius of the field, the entire field is accessible by the goat.

If the rope had a length equal to the radius of the field, the goat could graze approx 39.1% of the field.

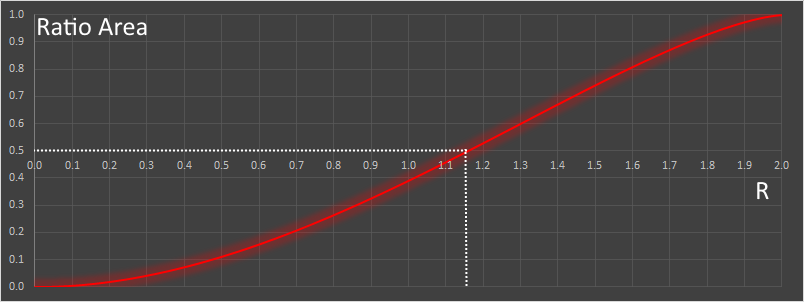
Solving for A=π/2 (a coverage area half the area of a circle of unit radius, so area ratio = 0.5), gives a value of R ≈ 1.158728.

The rope should be approximately 1.16 times the radius of the field to allow the goat to graze half the field.

Extensions

What if the farmer tethered the goat, not on the circumference of the field, but at some other arbitrary point?

These asymetric circle-circle intersection problems are interesting to investigate. If a cirlce of radius r, overlaps a circle of radius R, and the centers of the circle are d apart, then the equation for the overlapping lens is:

"Goats in Space"

Moving to 3D, the volume of the lens formed by intersecting spherical caps of spheres of radius: r and R whose centers are a distance of d apart, is a slightly simpler:

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.