De Bruijn Sequences
|
Last year I wrote an article about 4-digit PIN codes. It became quite popular, and I even got asked to give a TEDX talk about it which you can watch here (shameless plug). The basis of the talk was that people are very predictable in the selection of their codes. Mathematically, whilst there are 10,000 ways that the digits 0-9 can be arranged into a four digit PIN, people’s selections are not random. Only 426 distinct codes are needed to guess over half the PINs in use! |
 |
Perfect World
Imagine, instead of being predictable, that people selected their codes entirely at random. If you wanted to guess the PIN of a four digit combination lock, you might have to walk through all 10,000 four digit combinations. Since there are four digits in each number, the worst case is that you’d have to type 40,000 key presses, and on average it would take you half this number.
 |
That’s a lot of key presses. Can you do better? Can you do it with less key presses? Well, if the lock is smart, no, you can’t do better. But some systems that accept PINs are less sophisticated. These less secure mechanisms don’t quantize the inputs in batches of four (or however long the code is), but instead simply look at just the last four keys pressed. |
An example of this in use is shown below. Imagine you entered the six digits 123479 into one of these systems. As the system examines just the last four digits entered, this string would give you three distinct (overlapping) unlock attempts.

This simpler system has the advantage of not having to worry about what state you are in when you start, or having to code in time-outs into the entry system. Without this simplification, if your code was 1234, but just before you tried to enter it, unbeknownst to you, someone else had entered 99 on the keypad. When you entered your PIN, the lock would interpret this as 9912 (fail), and then 34 (still a fail and waiting for more digits before telling you it failed). Examining just the last four digits solves this problem.
If our system supports overlapping numbers we can be more efficient in guessing. We can create an input stream that goes through all permutations, but requires less key presses. The question is, how much more efficient? What is the shortest sequence of numbers that we can go through in order to ensure that all possible combinations of the digits are seen? Is it possible to create a sequence that does not repeat any sub-sequence of codes?
Nicolaas Govert de Bruijn
 |
The mathematics, number theory, combinatronics and logic of these types of problems were studied extensively by a Dutch Professor called Nicolaas Govert de Bruijn (9 July 1918 – 17 February 2012). Sequences of these numbers are named after him as De Bruijn Sequences. The quick answer is that, yes, it is possible to make a non-repeating sequence of numbers that covers ever sub-sequence internally, just once. However, before we look at the PIN number solution, let's look at some simpler versions of the problem … Image Credit: Konrad Jacobs |
 |
Simpler Sequences
|
De Bruijn sequences can be described by two parameters:
These are typically describe by the representation B(k,n). For our PIN example, the notation would be B(10,4) |
 |
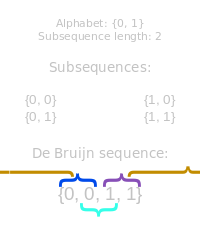
B(2,2)
|
Let's start with a really simple example: B(2,2) We'll use the dictionary {0,1} for the possible values. We want to generate a string that contains substrings each possible combination of two digits. Here is a solution: 0011 The first two digits give us 00, the next two 01, then 11. To get to 10, we need to 'Wrap Around' taking the last digit from the string, and the first digit. (If this is not appropriate to do, like the key-press example, then we can simply append the first character from the string to the end to make 00110). |
 |
 |
NOTE: There can be multiple De Bruijn solutions to any problem. You can easily see this using even simple rotations of the string. Since every adjacent pair of digits in this string is unique, it does not matter what the starting position is. As k and n increase, the number of possible solutions grows rapidly. The hairy looking equation on the left shows the number of distinct solutions. |
B(2,3)
Here's a solution for B(2,3):
00010111
Starting from the front, we have 000, 001, 010, 101, 011, 111, then staring to wrap around, we have 110 and finally 100. All eight possible combinations are present in this string.
B(2,4)
Here's a solution for B(2,4):
0000100110101111
You can see we have 0000, 0001, 0010, 0100, 1001 …
And here it is as a pretty ribbon. We can now hint at some of the awesome potential uses for these sequences. Imagine this De Bruijn sequence is written onto a looped tape, which passes past a reader head.
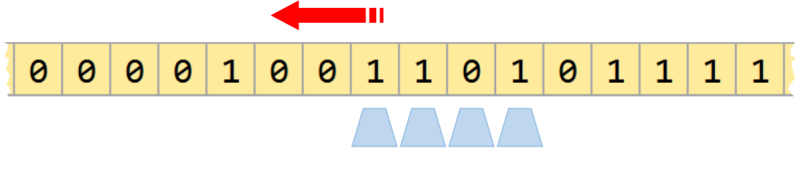
Each increment of the tape one position along gives a unique output. We have found an efficient mechanism of encoding position as there is a distinct code for any contiguous set of four digits (in this case, as n=4). How cool is that?
This sequence also walks through all permutations of combinations from 0000-1111. If you are a software engineer or tester, I'm sure this is giving you interesting ideas for how you can implement this as test cases to walk through all binary inputs to your functions. Each shift of one bit gives a unique binary word (of length of the substring size n), which does not repeat, goes through each possible number, then returns to the start again.
B(2,6)
Skipping ahead a couple, here is a solution for B(2,6):
0000001000011000101000111001001011001101001111010101110110111111
B(6,2)
Of course, we can also change the size of the dictionary. In this example rather than simple binary k=2, I've increased this to k=6 to use possible values {0,1,2,3,4,5}. Here is the output for B(6,2):
001020304051121314152232425334354455
Reading this from left to right we can see that we have: 00, 01, 10, 02, 20 … 41, 15 … 33, 34 … 55, 50
B(5,3)
One last example, here's a sequence for B(5,3):
| 00010020030040110120130140210220230240310320330340410420430441112113114122123124132133134142143144222322423323424324433343444 |
Back to PIN
Returning to our PIN cracking, the B(10,4) is 10,000 digits long, and contains every single substring for each combination of digits. As we have to type in this string, the concept of Wrap-Around is meaningless, so rather then wrap-around, we simply add the first three numbers again to the end of the strong. So, the maximum number of keypress events is 10,003. Far fewer than the 40,000 that would be required if typing them in completely!
For no useful reason at all, here are all 10,003 digits of this string:
| 0000100020003000400050006000700080009001100120013001400150016001700180019002100220023002400250026002700280029003100320033003400350036003700380039004100420043004400450046004700480049005100520053005400550056005700580059006100620063006400650066006700680069007100720073007400750076007700780079008100820083008400850086008700880089009100920093009400950096009700980099010102010301040105010601070108010901110112011301140115011601170118011901210122012301240125012601270128012901310132013301340135013601370138013901410142014301440145014601470148014901510152015301540155015601570158015901610162016301640165016601670168016901710172017301740175017601770178017901810182018301840185018601870188018901910192019301940195019601970198019902020302040205020602070208020902110212021302140215021602170218021902210222022302240225022602270228022902310232023302340235023602370238023902410242024302440245024602470248024902510252025302540255025602570258025902610262026302640265026602670268026902710272027302740275027602770278027902810282028302840285028602870288028902910292029302940295029602970298029903030403050306030703080309031103120313031403150316031703180319032103220323032403250326032703280329033103320333033403350336033703380339034103420343034403450346034703480349035103520353035403550356035703580359036103620363036403650366036703680369037103720373037403750376037703780379038103820383038403850386038703880389039103920393039403950396039703980399040405040604070408040904110412041304140415041604170418041904210422042304240425042604270428042904310432043304340435043604370438043904410442044304440445044604470448044904510452045304540455045604570458045904610462046304640465046604670468046904710472047304740475047604770478047904810482048304840485048604870488048904910492049304940495049604970498049905050605070508050905110512051305140515051605170518051905210522052305240525052605270528052905310532053305340535053605370538053905410542054305440545054605470548054905510552055305540555055605570558055905610562056305640565056605670568056905710572057305740575057605770578057905810582058305840585058605870588058905910592059305940595059605970598059906060706080609061106120613061406150616061706180619062106220623062406250626062706280629063106320633063406350636063706380639064106420643064406450646064706480649065106520653065406550656065706580659066106620663066406650666066706680669067106720673067406750676067706780679068106820683068406850686068706880689069106920693069406950696069706980699070708070907110712071307140715071607170718071907210722072307240725072607270728072907310732073307340735073607370738073907410742074307440745074607470748074907510752075307540755075607570758075907610762076307640765076607670768076907710772077307740775077607770778077907810782078307840785078607870788078907910792079307940795079607970798079908080908110812081308140815081608170818081908210822082308240825082608270828082908310832083308340835083608370838083908410842084308440845084608470848084908510852085308540855085608570858085908610862086308640865086608670868086908710872087308740875087608770878087908810882088308840885088608870888088908910892089308940895089608970898089909091109120913091409150916091709180919092109220923092409250926092709280929093109320933093409350936093709380939094109420943094409450946094709480949095109520953095409550956095709580959096109620963096409650966096709680969097109720973097409750976097709780979098109820983098409850986098709880989099109920993099409950996099709980999111121113111411151116111711181119112211231124112511261127112811291132113311341135113611371138113911421143114411451146114711481149115211531154115511561157115811591162116311641165116611671168116911721173117411751176117711781179118211831184118511861187118811891192119311941195119611971198119912121312141215121612171218121912221223122412251226122712281229123212331234123512361237123812391242124312441245124612471248124912521253125412551256125712581259126212631264126512661267126812691272127312741275127612771278127912821283128412851286128712881289129212931294129512961297129812991313141315131613171318131913221323132413251326132713281329133213331334133513361337133813391342134313441345134613471348134913521353135413551356135713581359136213631364136513661367136813691372137313741375137613771378137913821383138413851386138713881389139213931394139513961397139813991414151416141714181419142214231424142514261427142814291432143314341435143614371438143914421443144414451446144714481449145214531454145514561457145814591462146314641465146614671468146914721473147414751476147714781479148214831484148514861487148814891492149314941495149614971498149915151615171518151915221523152415251526152715281529153215331534153515361537153815391542154315441545154615471548154915521553155415551556155715581559156215631564156515661567156815691572157315741575157615771578157915821583158415851586158715881589159215931594159515961597159815991616171618161916221623162416251626162716281629163216331634163516361637163816391642164316441645164616471648164916521653165416551656165716581659166216631664166516661667166816691672167316741675167616771678167916821683168416851686168716881689169216931694169516961697169816991717181719172217231724172517261727172817291732173317341735173617371738173917421743174417451746174717481749175217531754175517561757175817591762176317641765176617671768176917721773177417751776177717781779178217831784178517861787178817891792179317941795179617971798179918181918221823182418251826182718281829183218331834183518361837183818391842184318441845184618471848184918521853185418551856185718581859186218631864186518661867186818691872187318741875187618771878187918821883188418851886188718881889189218931894189518961897189818991919221923192419251926192719281929193219331934193519361937193819391942194319441945194619471948194919521953195419551956195719581959196219631964196519661967196819691972197319741975197619771978197919821983198419851986198719881989199219931994199519961997199819992222322242225222622272228222922332234223522362237223822392243224422452246224722482249225322542255225622572258225922632264226522662267226822692273227422752276227722782279228322842285228622872288228922932294229522962297229822992323242325232623272328232923332334233523362337233823392343234423452346234723482349235323542355235623572358235923632364236523662367236823692373237423752376237723782379238323842385238623872388238923932394239523962397239823992424252426242724282429243324342435243624372438243924432444244524462447244824492453245424552456245724582459246324642465246624672468246924732474247524762477247824792483248424852486248724882489249324942495249624972498249925252625272528252925332534253525362537253825392543254425452546254725482549255325542555255625572558255925632564256525662567256825692573257425752576257725782579258325842585258625872588258925932594259525962597259825992626272628262926332634263526362637263826392643264426452646264726482649265326542655265626572658265926632664266526662667266826692673267426752676267726782679268326842685268626872688268926932694269526962697269826992727282729273327342735273627372738273927432744274527462747274827492753275427552756275727582759276327642765276627672768276927732774277527762777277827792783278427852786278727882789279327942795279627972798279928282928332834283528362837283828392843284428452846284728482849285328542855285628572858285928632864286528662867286828692873287428752876287728782879288328842885288628872888288928932894289528962897289828992929332934293529362937293829392943294429452946294729482949295329542955295629572958295929632964296529662967296829692973297429752976297729782979298329842985298629872988298929932994299529962997299829993333433353336333733383339334433453346334733483349335433553356335733583359336433653366336733683369337433753376337733783379338433853386338733883389339433953396339733983399343435343634373438343934443445344634473448344934543455345634573458345934643465346634673468346934743475347634773478347934843485348634873488348934943495349634973498349935353635373538353935443545354635473548354935543555355635573558355935643565356635673568356935743575357635773578357935843585358635873588358935943595359635973598359936363736383639364436453646364736483649365436553656365736583659366436653666366736683669367436753676367736783679368436853686368736883689369436953696369736983699373738373937443745374637473748374937543755375637573758375937643765376637673768376937743775377637773778377937843785378637873788378937943795379637973798379938383938443845384638473848384938543855385638573858385938643865386638673868386938743875387638773878387938843885388638873888388938943895389638973898389939394439453946394739483949395439553956395739583959396439653966396739683969397439753976397739783979398439853986398739883989399439953996399739983999444454446444744484449445544564457445844594465446644674468446944754476447744784479448544864487448844894495449644974498449945454645474548454945554556455745584559456545664567456845694575457645774578457945854586458745884589459545964597459845994646474648464946554656465746584659466546664667466846694675467646774678467946854686468746884689469546964697469846994747484749475547564757475847594765476647674768476947754776477747784779478547864787478847894795479647974798479948484948554856485748584859486548664867486848694875487648774878487948854886488748884889489548964897489848994949554956495749584959496549664967496849694975497649774978497949854986498749884989499549964997499849995555655575558555955665567556855695576557755785579558655875588558955965597559855995656575658565956665667566856695676567756785679568656875688568956965697569856995757585759576657675768576957765777577857795786578757885789579657975798579958585958665867586858695876587758785879588658875888588958965897589858995959665967596859695976597759785979598659875988598959965997599859996666766686669667766786679668766886689669766986699676768676967776778677967876788678967976798679968686968776878687968876888688968976898689969697769786979698769886989699769986999777787779778877897798779978787978887889789878997979887989799879998888988998989999000 |
How do these things work?
I glossed over how to calculate a De Bruijn sequence earlier. I'll make up for it now by explaining the principles for how these things work. The concept is not complicated, just tedious; things that computers can do easily. We're going to look at this problem using Directed Graphs.
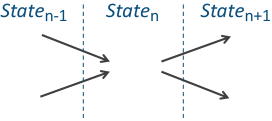 |
For this example, I'm going to use B(2,3). This sequence is simple enough to get the concept without being too complex and busy. Every sub-string in the sequence can be described as a node on a directed graph. From each node, it is possible to add either a 0 or a 1 to make the next number in the sequence. Similarly, each state/node on the graph could have been formed from adding a digit from one of two earlier states. |
|
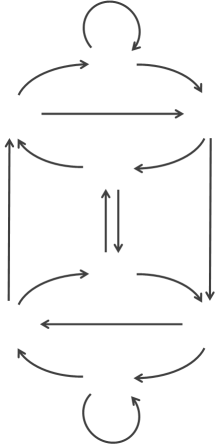
First we write down all the nodes that are possible using our data dictionary. In this case these are 000 - 1111. Then we connect the nodes with lines showing which possible next states are achievable from each location. Each node has two outbound links corresponding to the addition of a 1 or 0 from that state. These edges are directed. They have a direction (depicted by the arrows) Note - For States 000 and 111, the addition of a 0 or 1, respectively, takes you back to the same node. |
 |
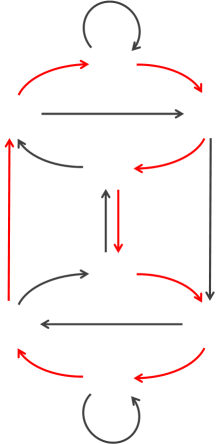 |
In order to make sure every substring is present in the solution, we need to make sure each node is passed through once (and only once). We need to trace a path through the graph (following the arrows) to connect the nodes. A path that traverses a graph and visits each node exactly once is called a Hamiltonian Path. One such Hamiltonian Path on the B(2,3) graph is shown in red on the left. This highlights why there are many different solutions (not just rotations). There is more than one way to walk through this graph. The way to create a De Bruijn sequence is to find a Hamiltonian Path through a graph their nodes. |
|
As the values of k and n increase, so does the complexity of the graph, but the principle is the same. Here's a slightly more complex one using a dictionary {1,2,3) for a sequence B(3,2) Find a path through the graph the passes through each node just once, and you have your solution. |
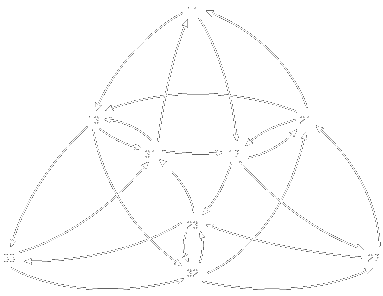 |
Other uses
We already hinted that De Bruijn sequences can be used for encode/decode positions, and that they can be used by savvy computer programmers. What are some other applications?
 |
I’ve seen magicians use a similar principle in various card tricks. By pre-arranging (loading) a deck with a known sequence of red and blacks cards in a De Bruijn sequence, it allows him/her to know what the position is, and thus, what the next card will be. Using a binary encoding of the red/black cards to generate a unique number, which can then, be used to encode the value of what the next card will be. |
Because of the wrap-around nature of De Bruijn sequences, a loaded deck can be cut as many times as desired without upsetting or disturbing the encoding. I don't want to link directly examples, as I don't want to ruin the tricks for others that might be performing them, but I'm sure if you know how to use a web search tool, you can find some strategies.
DNAThe concept of Hamilton cycles and De Bruijn are used extensively in modern DNA sequencing techniques. A large DNA chain can be broken up into smaller pieces (The smaller pieces being easier to process and sequence). Then, the results of these smaller pieces can be 'glued' back together like some kind of giant jigsaw because the individual sub-pieces contain overlaps with other partial strings. This technique is called Shotgun Sequencing. |
 |
Below you can see a representation of a long chain of DNA. This is smashed into smaller sub-pieces (of different sizes), which are easier to classify. The classified pieces can then be joined back together to form the complete sequence by looking at the overlaps between the substrands.
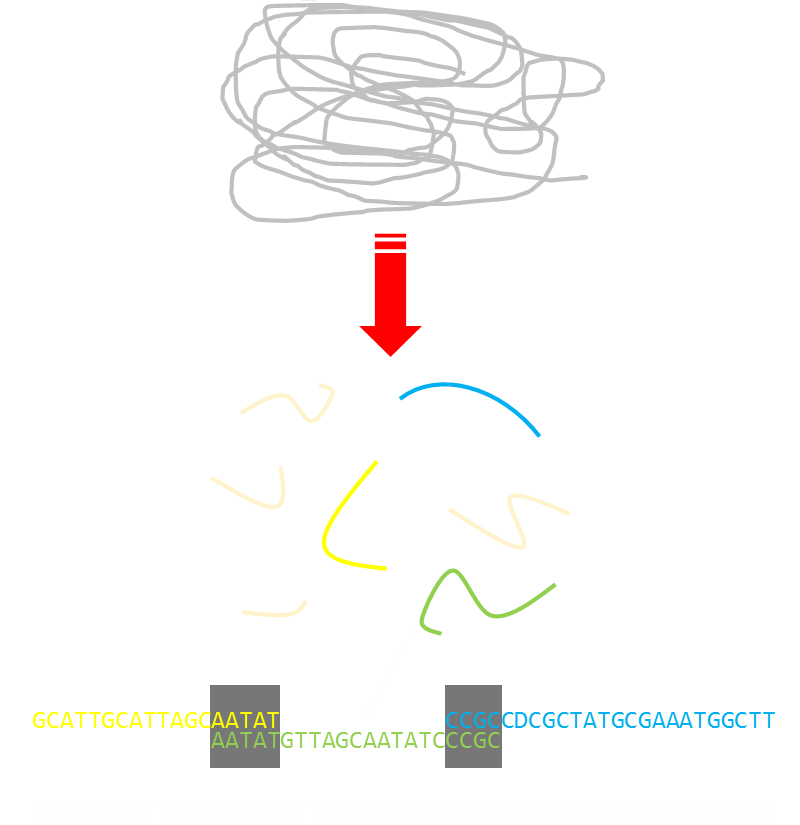
In some cases, the shotgun sequencing technique generates multiple canonical sequences. Of course, only one of these can be the real sequence. There are a variety of tests that can narrow down which of these sequences is the original one. Shotgun sequencing, although it does not necessarily define the exact sequence, greatly speeds up the process by reducing the number of possible candidates.
The advent of shotgun sequencing techniques advanced the initial mapping of the human genome by years, and it has provided biologists, geneticists, and doctors with a powerful new tool. The ability to sequence genetic data rapidly has potential benefits not only for life and health science professionals, but also for the public at large. It's pretty cool.
Chess
Computer programs that play chess make use of De Bruijn sequences. A chess board is conveniently 8 x 8 squares, and these can be represented by the numbers 0-63, which is a nice fit for a six bit long De Bruijn sequence.
De Bruijn Toroids
OK, prepare your mind for something cooler still. We can expand a De Bruijn one dimensional sequence into two dimensions! We call these Toroids because every row and column wraps around onto itself.
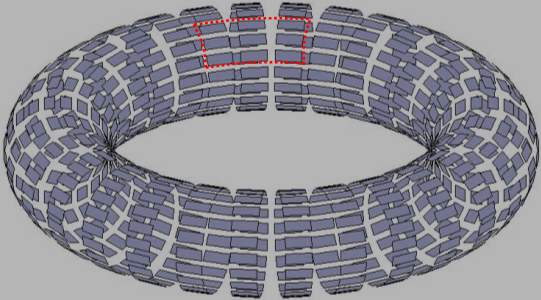 |
Sliding a window over this surface creates a unique matrix for a well-formed De Bruin array. Things get much more complicated because not only do we need to specify the number of items in the dictionary, but also the two dimensions of the window. |
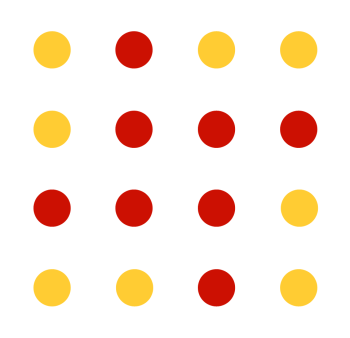
Below is a simple example of an array that has a dictionary of two {red, yellow}, and a (2 x 2) window:
|
If you look carefully, you will see that every combination of red/yellow dots appears all possible combinations of (2x2) sub-matrices. Remember, you need to wrap-around (for instance to get a matrix containing four yellow dots you need the matrix that is the four corners wrapped around the outside!) I'm sure you can see instant applications for something like this in determining (x,y) position. Each window is unique and determines coordinate position. |
 |
Of course, we're not restricted to using just a dictionary of two items. Below are two larger De Bruijn toroids. The one on the left has a dictionary size of three, and matrix window of (2 x 2). The one on the right has the same matrix window and this time has a dictionary of size four.
 |
 |
The grid on the left is (9 x 9) and that on the right is (16 x 16), allowing representation of all 256 possible combinations that a dictionary of order four into a (2 x 2) matrix. De Bruijn Toroids also don't have to be square; for instance there is a solution the four dictionary solution that fits in a matrix (8 x 32) instead of (16 x 16).
Of course there are multiple equivalent translations of these solutions as any combination of row or column shift is a valid solution. It's also possible to tesselate these tiles perfectly edge to make a map the repeats with the same order frequency.
Digital Paper
 |
Anoto, a Swedish company, has invented, and has numerous patents, concerning the use of digital pens and paper. The Anoto concept is based around a distinct pattern of dots that can be printed onto paper stock. Using a special pen, which contains a small camera, the dot pattern can be read, and exact position on the paper determined. Whilst not quite the same concept, the Anoto system works by small changes in the displacement in the position of dots from a nominal mean position. |
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.

