
	Advertisement

Cutting a semi-circle

A little puzzle to round the month out. We start out with a unit semi-circle:

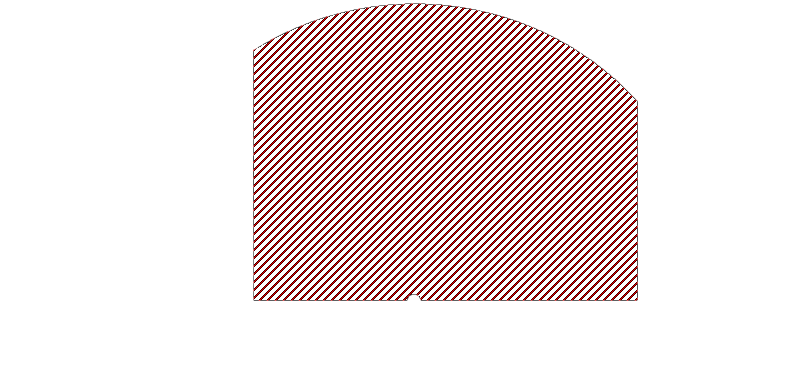
Q: What is the area of the red shaded region below bounded by:

I could think of two alternative ways of solving. One using geometry, and the other using calculus. The calculus solution is signficantly more involed but, thankfully, both methods return the same result!

Will you take the red pill, or the blue pill?

Geometry

Calculus

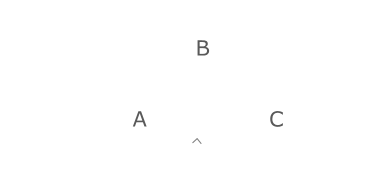
To solve geometrically, we can break the shaded region into three pieces: A, B, C

A and C are triangles (with complimenatry angles), and B is a quarter circle segment with unit radius.

The area of both triangles turns out to be the same (half the base times the vertical height). Summing up these three regions gives us the answer.

Because we know the equation of the semi-circle, and the limits, we can use integration to find the area underneath the curve.

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.