
	Advertisement

There and Back Again

There and Back Again (and non-Conservative paths)

Here’s a thought experiment for you:

Let’s imagine you visit an airport, with your twin, and the terminal has one of those travelator moving walkways. The travelator runs the length of the terminal.

Photo Credit: Andy Teo - photocillin

You stand directly in front of the travelator, and your twin stands a few feet away, directly in front of the parallel walkway.

You then start a race. Your twin walks down the walkway all the way to the end of the terminal, turns around and walks immediately back, reversing his/her path.

Starting at the same time, you walk down the travelator to the end, then turn around and walk back, but this time walking back down it the wrong way. (just like you probably did when you were a kid!)*

You both walk the same distance.

Who wins the race?

*And maybe still do when nobody else is looking!

You can assume that you and your twin walk at exactly the same rate, the distance you both travel is the same, the travelator is traveling at the same constant speed, and you are traveling at speeds below which the effects of relativity are significant … This is not supposed to be a question where there are tricks, traps or gotcha’s.

Question: Who finishes first?

Does your twin finish first?
Do you finish first?
Or, does the boost you get from going with the flow on the way down, cancel out the headwind you suffer on the way back to make the race a dead heat?

The answer is that your twin will win the race. Every time!

That's right. A person who simply walks both directions will always win a race against someone who walks/rides in opposite directions on a moving platform. To see why we need a little algebra …

A little algebra

Remembering back to High School Physics, we recall that the time it takes to cover a distance, is this distance divided by the speed we travel:

If we define the distance to the end of the terminal as d and the speed at which you (and your twin) walk as S we can find the time it takes to simply walk to the end and back. We'll call this the Vanilla trip time. Because we have to walk there and back, time is represented by this formula:

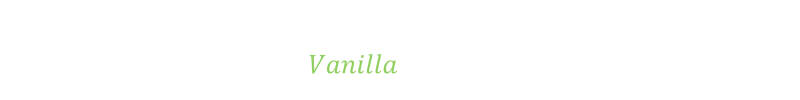
The time taken by your twin can similarly be calculated. If we represent the constant speed of the travelator as v, then it can be represented by the formula below. On the way down, the travelator speed is added to you speed S + v, and on the way back the travelator speed is subtracted from your speed S - v. We'll call this the Modified time.

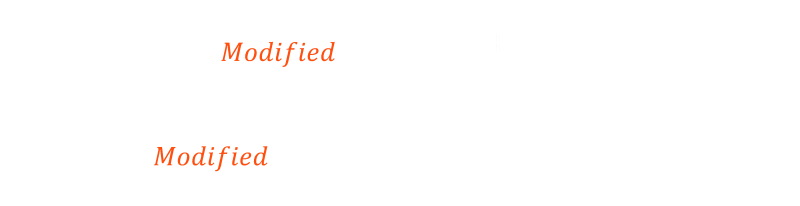
Expanding out, simplifying, a pulling out a 2d/S term out:

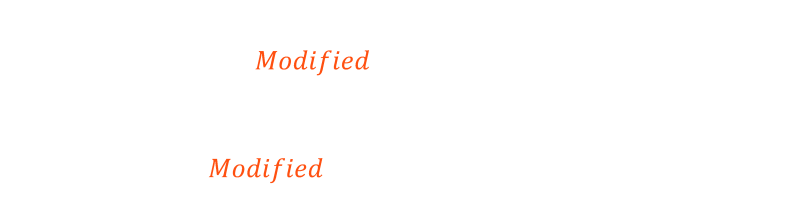
The right hand term can be re-arranged to show a ratio of (v/S)²

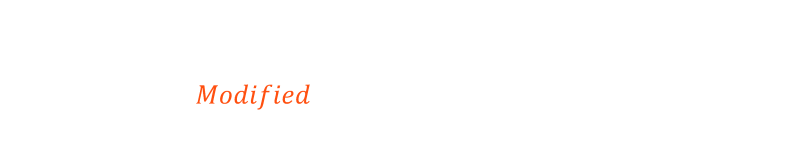
Finally we can divide the original Vanilla time by the Modified time to get a ratio of the two speeds.

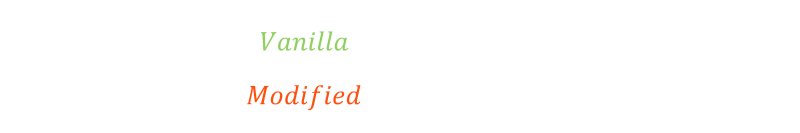
This is a very interesting result. Because the ratio (v/S) is squared, it is always positive. This means that right hand side of the equation is always less then 1.0 and so the Modified time is always greater than the Vanilla time. This is the proof we need.

Also of interest, is that the squaring of the (v/S) ratio means that it does not matter the sign (direction) of the travelator velocity. This makes sense as you think about it beacause, whatever the velocity of the platform, you'll be travelling on it in both directions!

Thinking about it

After thinking about this for a little while, it clearly makes sense. Whilst you might be travelling faster on the belt on the way down, this fact means that you will be travelling at this speed for a shorter amount of time. Similarly, on the way back, not only will you be travelling slower, you'll also be travelling at this slower speed longer.

Taking this to the extreme, imagine that the travelator is travelling at speed equal to the speed you walk. Sure, on the way down you'll whizz down the terminal, but on the way back, well, you'll never make it. You'll be on the World's largest treadmill; walking and not getting anywhere!

Road Trip?

A similar principle applies to the calculation of average speeds. Let’s imagine you are going on road trip that is 120 miles long. You estimate that your car will average 60 mph, so the trip should take you two hours. You need to be there at midday, so set out at 10:00 am.

However, there is traffic, and for the first half of the trip (60 miles), you only average 30 mph. What speed will you need to travel over the second half of the trip in order to get to the destination ontime?

Of course, it’s impossible. Travelling the first 60 miles at 30 mph has already burned the two hours up, and you’d need to travel infinitely fast over the next 60 miles to get there at midday.

Speed Records

According to the Fédération Internationale de l’Automobile, in order to be granted a land speed record, it's not just sufficient to obtain a high top speed. The feat has to be repeated by a run in the opposite direction within one hour. The average speed over these two passes is used to determine the speed record.

Photo Credit: Mark Nockleby - nocklebeast

The reason for runs in opposite ways is to remove any potential bias in one direction (such as wind, or a slight gradient of the slope).

As we now know, any kind of wind is detrimental to a land speed record. Any speed advantage gained driving with the wind is paid for more heavily driving against the wind. The overall average of the two passes is always reduced by any amount of wind.

If you're going for World Record, pray for a still day.

Running

Whilst most stadiums are pretty well shielded from the wind, the same effect can influence runners going around a track. Running with the wind may be easier, but the boost given is not enough to make up by the struggle against the wind on the opposite side of the circuit.

Planes, Trains and Automobiles

Photo Credit: Andrew Wilson - hkfuey97

A plane doing a return flight (there and back between two locations) will take longer for the total trip time if there is stronger wind than if there is a gentle wind (assuming the wind is constant).

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.