Langton's Ant (and Life)
|
If you grew up, like I did, writing code for fun, then there is good chance that you will have implemented some form of Conway’s Life on one of computers you owned (and maybe a Mandelbrot renderer, and a Sieve of Eratosthenes to calculate Prime numbers too … ?) If you are not familiar with Life, it’s a classic simulation, invented by John Conway in 1970. It’s a type of program given the fancy name of a Cellular Automaton, and it’s a crude approximation of life on a rectangular gridded Petri Dish. Cells (squares) are either occupied or empty. Cells states are determined by following a very small collection of simple rules (based on the state of their immediate neighbors). |
 |
Once an initial starting configuration has been setup, all rules are applied synchronously to make a new iteration, then again …

… it is the state of the eight neigbors around each cell that determine the fate of the center cell.
Wash, rinse, repeat …
 Glider Gun. Image: Johan G. Bontes Glider Gun. Image: Johan G. Bontes |
The cells (colonies), can change with each iteration. Sometimes they die out totally. Sometimes they continue growing and expanding forever (proven), and sometimes they reach a steady state (either static, or oscillating between a series of fixed states with a common time-base). There are many awesome sites on the web dedicated to Life, and some viciously optimized implementations that allow you to experiment with gigantic layouts in times I could only dream about when I wrote my first version (in 6502 assembly). Go Google some and play, but for more fun, if you haven’t already, go implement a Life engine in your favorite programing language (I’ve even read about people implementing it in SQL!) |
Here's a nice JavaScript implementation with an enhancement option that allows you to color cells that have been visited at least once so that you can gauge expansion and contraction.
Rules
Here are the four rules used in classic Life:
Any live cell with fewer than two live neighbours dies, as if caused by under-population.
Any live cell with two or three live neighbours lives on to the next generation.
Any live cell with more than three live neighbours dies, as if by overcrowding.
Any dead (empty) cell with exactly three live neighbours becomes a live cell, as if by reproduction.
Common Static Patterns
If you play with Life for a little while, here are some common patterns that you'll see occurring. The first are a collection of stable (static) shapes. Unless interfered with by other elements, these objects remain stable and unchanging. They are given colloquial names by enthusiasts.
| "Block" | "Beehive" | "Loaf" | "Boat" |
 | 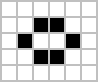 |  |  |
Images: Wikipedia
Other common shapes have names: Tub, Pond, Ship, Longboat, Barge, Mango …
A list of the commonly found shapes can be found here.
Oscillators
Next are some common (and some not so common) oscillators. These vacillate between states (sometimes changing mass), but do not translate over the grid.
Oscillators with periods of 2, 3, 4, 5, 6, 8, 14, 15 and 30 have been discovered to date.
| "Blinker"Period = 2 | "Toad"Period = 2 | "Beacon"Period = 2 | "Pulsar"Period = 3 | "Pentadecathlon "Period = 15 |
 |
 |
 |
 |
 |
Spaceships
| "Glider" | "Lightweight spaceship (LWSS)" | ||
|
The geometry of some patterns causes them to move and translate across the grid. Two of the simplest are shown to the right. The Glider (the smallest possible stable moving ship), moves diagonally. The LWSS translates purely in one coordinate direction. |
 |  |
Turing Machine
 |
Streams of spaceships can be arranged to collide and intersect with other elements to give different results depending on the number of spaceships present. It's possible to arrange elements to make fundamental logic gates such as AND, OR, and NOT, and a finite state machine. Simply put, this simple cellular automaton is can be configured into a computer! And, as it is Turing complete, given a massively large grid and timebase, there is no reason it could not perform the same calculations as the computer you are reading this web page on! |
Life is computer!
Langton's Ant
A different flavor of cellular automaton was described by Chris Langton, in 1986, and this is named after him as Langton's Ant.
 |
The rules for Langton's Ant are even simpler than Conway's Life. An ant sits on a particular square of the grid. If the square it is currently sitting on is set, it turns right (a quarter turn) then moves one space forward (unsetting the state of the cell as it leaves). If the square it is currently sitting on is unset, the it turns left and moves forward one space (setting the state of the cell as it leaves). That's it! The rules are that simple. On every move the state of the square the ant was occupying is toggled (set/unset). Every time-tick it turns 90° and moves forward one space, and it's only the state of the current square that determines if it turns left or right. In the animation on the left, black is used to identify cells that are 'set' and white for 'unset'. The red arrow shows the direction the ant is facing when it is in each cell (not the direction it's going to move). |
What happens?
 |
Something interesting happens. Initially the patterns formed are very simple, and often go through cycles of symmetry. However, after a few hundred steps things start to turn chaotic and the image starts to look random. Finally just before 11,000 steps, structure appears and an emergent pathway appears out of the chaos. This pathway is formed as a stable repeating pattern of base approx 100 operations that translates across and down and continues in this form forever. |
Try it out
Below is a short applet to allow you to try it out. The top button starts and stops the animation, and below this is the option to reset the simulation.
The button marked 'Random' can be pushed at any time (and multiple times if desired) and runs through the grid toggling the state (set/unset) of every square with a 1:200 chance; Adding random elements can distort how long before emergent behaviour appears. The grid button determines if the square grid is rendered.
The number of steps taking in by the ant is shown in large digits in the lower right.
NOTE - Progress stops as soon as the ant walks off the grid, and if too many random elements are present, it might not have reached emergency before the animation stops.
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.

