Rope Swing
|
This evening I was watching American Ninja Warrior on TV with my son. The contestants are very skilled athletes. I’ve not watched the show religiously, but the few times I have seen it, there is an ever changing range of obstacles to overcome On this particular episode, one of these obstacles involved swinging on a rope from a raised platform with the intention of getting safely across a pit.
This made me think. What is the optimal strategy for letting go of a rope to maximize the horizontal distance travelled? Let go too soon, and you might have a lot of horizontal speed, but you’ll be a long way from the landing zone (and be low down when you release). Let go too late, and whilst you’ll be closer to target (and higher), you’ll have low horizontal momentum. Somewhere in between there must be an optimal release point. |
 Image: blythe83
Image: blythe83 |
What is the optimal strategy for letting go of a rope to maximize the horizontal distance travelled?
If anyone has played on a rope swing over a river or pond, it’s the same problem. Where should you let go of the rope so as to get as far out into the water as possible?
It’s not a trivial problem. In fact (as we will see), the math is quite complicated and depends on many variables.
Where should you let go?
Imagine you are standing on a platform holding onto the end of a a taut rope. You grab the rope, lift up your feet, and swing out over the lake. If we neglect the effects of air resistance, assume the rope has no mass and acts like stiff pendulum, and say that you didn't have any forward momentum before you lifted up your feet, at what point should you let go of the rope to get the greatest distance away from the platform by the time you hit the water?

After your lift up your feet, you'll swing like a giant clock pendulum, accelerating downwards. You trade your gravitational potential energy into kinetic energy. At the bottom of the swing you'll be travelling the fastest and then, as you gain altitude, you trade the energy back and you start to slow down again.
 |
 |
 |
At some point, you'll let go and the horizontal component of your velocity will keep you moving forward. Gravity will pull you down from the height you've achieved, but you'll get some assistance from the vertical component of your velocity. Wheeeeeeee!
Before letting go of the rope, you'll be describing a circular arc. After letting go you'll be on a parabola (more of this later). The distance you travel will depend on both the height of the platform and also how far above the surface of the water the end of the rope is (again more of this later).
Let's tackle this problem in stages …
No height difference
When we are hung on the rope, we are constrained. There is nothing we can control, the tension in the rope provides the centripetal force required to pull us in a circular arc. We can, however, elect when to let go. This will be at a certain angle and there will be a correlated velocity. Ignoring this correlation for a moment, what is the optimal angle for departure if there is no height difference?

This is a classic physics (ballistics) problem. It's equivalent to asking the question about what the optimal angle is to throw a spear (or fire a canon), to get the greatest distance. If a projectile is given an initial velocity v, what angle θ results in the greatest distance R?
As we are ignoring air resistance, the only force acting on the projectile is gravity. The horizontal component of the velocity remains constant, and integrating this over time gives the distance R. The equation for the horizontal distance travelled can be described by:
In the vertical plane, the component of velocity is initially upwards, then is decelerated by gravity. This gives us another equation which we can rearrange to get the time of flight t which we can substitute back into the first equation.
The equation above gives the distance travelled R as function of the angle of launch θ
To find the maximum, we take the first differential with respect to the angle and set this to zero to represent the turning point. (The second differential is negative, showing this point is a maximum turning point).
The only 'sensible' angle for this turning point is π/4 which is 45°. This is the optimal angle.
If there is no difference in altitude between the launch point and the landing point, the furthest distance is obtained by releasing from an angle of 45°
Height Difference
If there is a height difference, things get a little more complicated. Now there is an additional variable h:

The equation for the horizontal component remains the same:
The projectile, however, now needs to travel in the vertical plane by distance h.

(We're going to take just the positive root, as this is the only one that is sensible! We're not concerned with the solution if were were able to tunnel through the cliff we are standing on backwards to water level the other way.).
Here is the equations for the range in the direction we're looking:
To find the maximum, we differentiate, and set this to zero to find the turning point in the gradient:
There's got to be an easier way of doing this, but we've started, so we might as well plough through it:
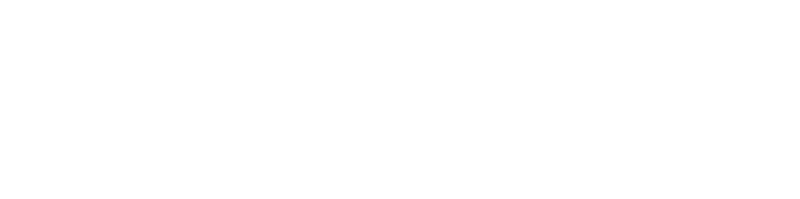
That's pretty scary looking, but with the application of a trig identity we can start expanding out, and terms start to cancel:
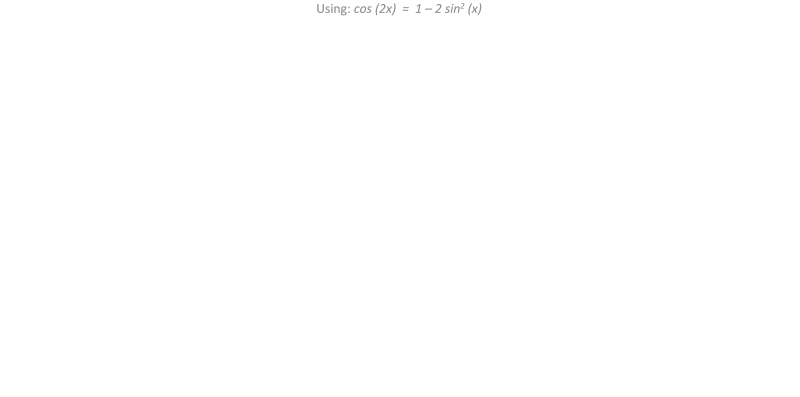
At last, we get an equation that gives the angle for the maximum distance when there is an altitude difference!
This equation gives us some interesting results. First, when h=0 (when there is no altitude difference), then the sin(θ) term reduces to 1/√2, which is 45° and confirms our first result. (Phew!)

|
The second result is that, when h is positive, the value for θ will always be less than 45°. Out of all the possible parabolic paths (such as those depicted on the left), the optimal angle to shoot, if the target is below the shooter, will always be lower than the optimal angle on a flat surface. As we will be releasing from the rope when it is above the water (there is some way to drop), we'll always be releasing the rope before 45°. |
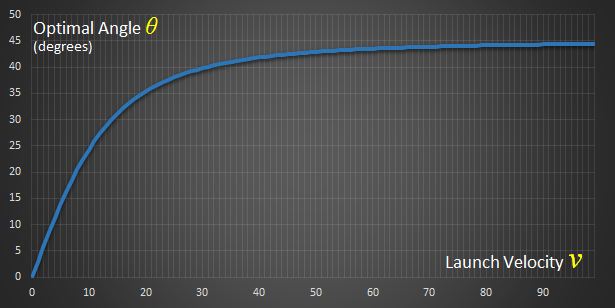
Below is an example graph of how the optimal angle changes with launch velocity. (In this example, I'm assuming a 20m cliff, with launch velocity measured in m/s). When the velocity is low, the angle is shallow. Ever possible speed is given to the particle to get it away from the cliff before is it falls. As the launch velocity increases, so does the angle, asymptoting to 45° at high speed.
The converse happens when h is negative (if we were attempting to throw a rock up onto a shelf and get it the greatest distance away from the edge). For these cases, the angle would always he greater than 45°
You should also be able to see that if h becomes too negative relative to v, there is speed, below which, it is impossible to reach the shelf. This is intuitive and backed up by the formula as arcsin() is not defined for a value > 1.0 (If the ledge is too high up, there is no angle which you can launch a low velocity projectile to reach it!)
Back to the rope
OK, now we are back to the rope swing. The mechanics depend on the geometry of the swing.
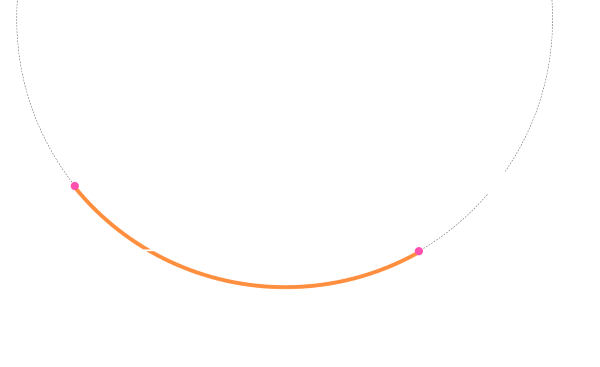
The rope is length r, and the position of it's anchor determines the shape of the arc. An easy way to describe this is by the angles subtended by the swing. We can define the angle from the staring location to the lowest point of the swing by α and the angle from this nadir as θ (this will be the same angle as the launch angle from release point).
 |
The horizontal distance travelled by the swinger is the distance travelled when on the rope, plus the distance travelled in the air. 
The vertical distance is the height adjusted by geometry of the swing and and point of release of the rope. This can be combined into an equation of motion similar to before with just a modified height. 
|
As before we can use the quadratic root solver (and take just the positive radical) to determine the time of the parabolic part of the episode:

We can substitute this value for time into our first equation and we now have a description of the distance travelled in terms of the geometry and gravity, but we still have one extra variable, and this is the velocity v, a the release point of the rope:
The path whilst on the rope is constrained to a circular arc, and we can determine the velocity at the release point with a simple calculation of conservation of energy. Starting at the top, the swinger has potential energy, and converts this (forewards and backwards) into kinetic energy. The difference in height between the start and release points determines the change in energy. This is similar to the calculation we did on Roller Coasters.
Now we know the velocity at release we can insert this to make a Klingon Battle Cruiser of an equation:
Analysis
I don't know about you, but I've had enough calculus for one day, so let's look at examining this equations numerically and see what we can determine. The longer the rope, the longer the distances, and it is the difference in height between the launch point and release point that determines the release speed. The higher the launch point over the water, the shallower the release angle. Let's see how these affect things.
When you encounter a rope swing in the wild, the geometry is already determined for you. The launch height h is fixed, and so is the length of the rope r and the launch angle α.
Plotting it out
To help compare how things change, we'll look at normalizing all distances as a ratio of the length of the rope r.
So, we'll measure the height of the launch platform interms of h/r, and the distance travelled as R/r.
Below is a graph of one extreme, and is a plot of distance travelled based on the release angle. On the x-axis are depicted all angles from 0° to 90°. On the y-axis is the distance obtained (as a ratio of the length of the rope).
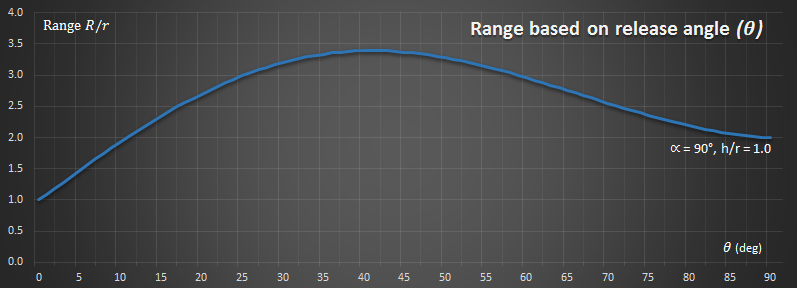
In the above graph, I set h/r = 1 (the rope is the same length as the height of the launch platform), and also α = 90° (the rope will swing a quarter circle). There are some obvious things we can see from this (which thankfully confirm common sense!):
When the launch angle as 0°, the Range is 1. This is what we'd expect. The rope swings down a quarter of a circle and just reaches the water (a distance the 1 away from the platform). If you let go here, you'll instantly be in the water and travel no further!
As the release angle increases past zero degrees, we rise over the nadir and after release have some height to play with as well as forward velocity. Range increases.
Range increases, as predicted until a maximum of just before 45° (it's not exactly 45°, because we started at a higher altitude than the water).
After this maximum, range decreases again. We get more height from the release, but less distance overall.
Finally, at the other extreme, at a 90° release point, we've no forward velocity anymore. Letting go at 90°, and you'll simply fall vertically into the water! The distance travelled be this technique is, as expected, twice the radius.

As the starting angle decreases, the shape of the curves change. Keeping the height of the platform constant with respect to the length of the rope, here are curves for various ranges of α. With smaller α the velocity at the release point is also lower.
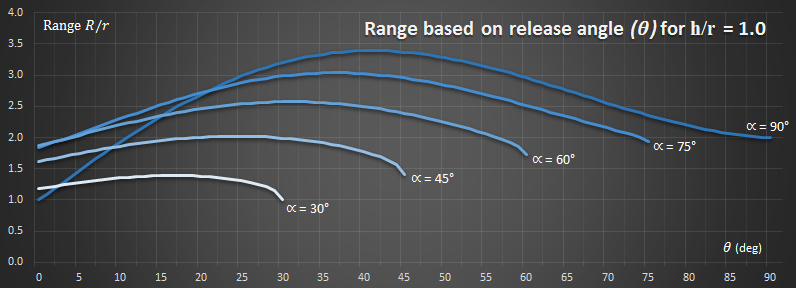
As the starting angle decreases, so does the range of possible launching angles. Because of conservation of energy, it's impossible to launch from an angle higher than you started from!
 |
As α changes, so does position of the nadir. The radius of the rope circle stays constant, but to get the required drop angle, this is equivalent to moving the attach point of the rope upwards and closer to platform. Whilst the upwards movement gives additional height, it puts the release point further back. This leads to some interesting extreme results, in that, when the geometry is such that the swing drops close to the water, such as very high α, at low angles of release, less distance can be obtained than with shorter starting angles, because the release points will be so close to the water. This is why, in the graph above, the curve for 90° crosses over the other curves at low release angles. |
As the height of the launch platform increases, this becomes less important. Here are three graphs with various values of h/r.

As height increases (relative to the rope length), the optimal release angle decreases. At the far extreme (when the starting angle and release angle are the same), the distance travelled is the same, irrespective of the height of launch. At this point, you are letting go of the rope at the end of the swing, have no horizontal velocity, and simply fall vertically down.
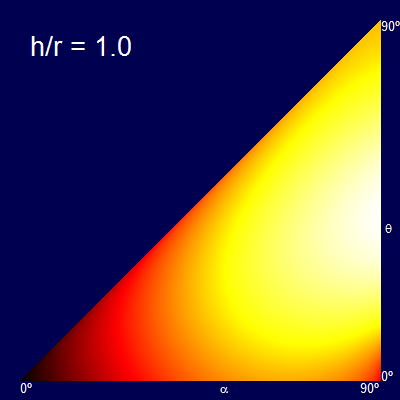
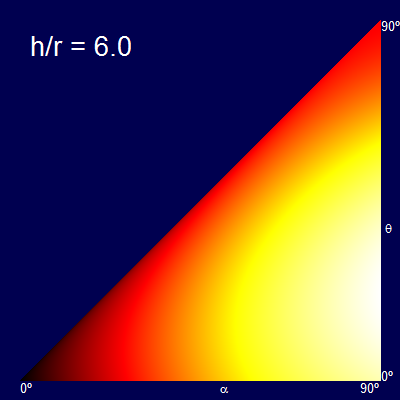
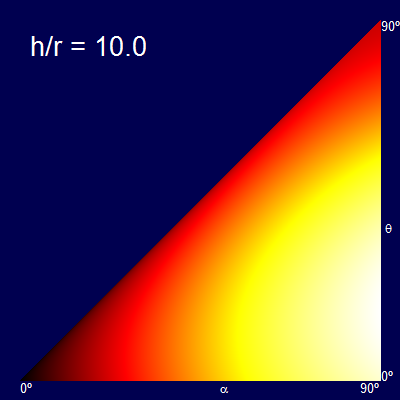
Another way to represent this is by heatmaps of the distance obtained for each combination of α and θ. The dark colors represent the short distance, and the bright colors the longer distances (The palette of each graph is normalised for just that graph).
The x-axis shows the swing angle, and the y-axis shows the release angle. For example plots below are shown for various rations of h/r.
 |
 |
 |
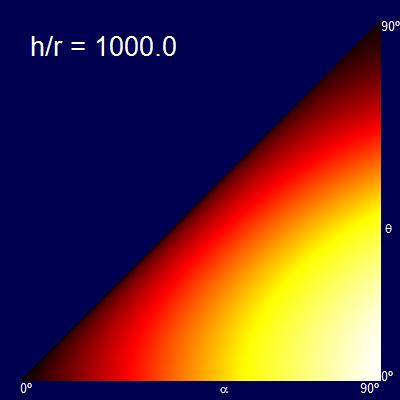 |
When the h/r ratio is small, the optimal release angle is close to 45°. As the height increases the release angle decreases, limiting to the ridiculous case that you let go of the rope at the bottom of the swing and travel entirely horizontally (the fall being so high at this point that there is no advantage in trying to gain any additional altitude, and all possible speed should be in the component getting you away from the launch point).
Another way of thinking about this is that a vertical stripe through the triangular plots gives the profile curve of the graphs created before. (The graphs are triangular because it is impossible to release at a higher angle than the starting angle).

Practical Advice
A quick glance of photos on the internet shows that most real rope swings have quite a long rope in relation to their platform height.

Image: nate bolt
 |
If we estimate a launching height of approximately 3m (approximately 10 ft drop), with a 12m (40 ft) rope, this gives us an h/r ratio of 0.25 Also, a quick glance of the internet shows that a good approximation for the starting angle is 30° |
Plugging these values in gives a distance/launch angle curve like this below. The optimal angle for this configuration is a release angle of approximately 23.75°. The veclocity you will be travelling at release time is approximately 3.4 m/s.
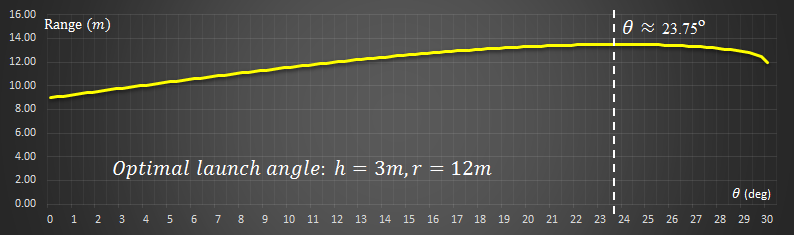
What does the flight profile look like? Something similar to this below. Based on common observed geometry of rope swings, the release point is pretty close to the end of the swing. (But, of course, now you know how to calculate your optimal release point if you encounter a swing with non-traditional geometry …)
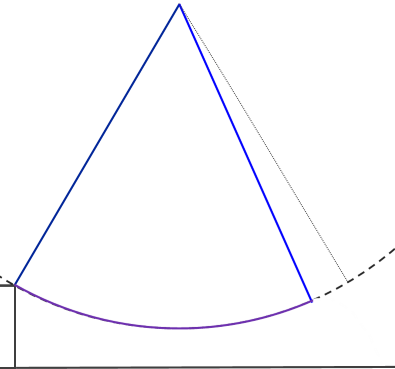
|
 Image: blythe83 Image: blythe83 |
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.

