A "Practical" use for Genetic Programming
I love to write code. Sometimes there is a purpose, sometimes it is just for fun.
After reading an article on genetic programming, I wanted to experiment with the concept but had no immediate need, so I invented one! I decided I would use the concepts to teach my computer how to paint a picture of me.
Below is a picture of me that was taken at a photo-shoot for another venture of mine GreatPokerHands (an easy to use poker strategy product to help you play better Texas Hold'em Poker).

I cropped the source image to 256 x 256 pixels. Each pixel in the image is represented by an RGB value using 8-bits for each colour, giving 256 levels for each primary colour. (Using nice powers of two makes the math and coding a lot simpler).
Genetic Programming
Genetic Progamming is inspired by biological evolution. It is a machine learning technique used to optimise a solution based on a fitness score. Solutions are represented by chromosomes encapsulating parameters, and these chromosomes change with iterations to get closer to a desired representation. Modeling real life, chromoses can breed (cross-pollinate), randomly mutate, and expire (die out).
The process
I decided to attempt to recreate my image, genetically, using just 32 rectangles. Each rectangle would be semi-transparent, and initially randomly placed. Then, using a genetic algorithm, I would modify the rectangles in an attempt to improve the quality of the final image.
Each rectangle in the destination image was represented by a gene that encoded the paramaters of the rectangle. The coordinates of two diametrically opposing corners specificed the size of the rectangle, and the RGB values represented the colour of the rectangle. These values were converted into binary and concatenated to form a long string of digits. 32 sets of these genes joined together formed one chromosome encapsulating all the details necessary to draw the image.
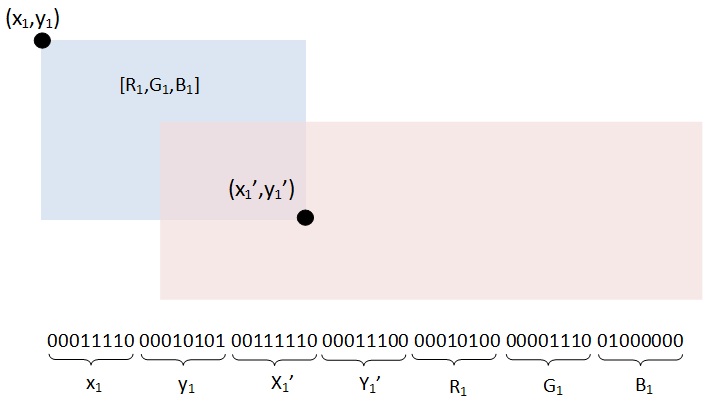
[GEEK ALERT] Because of the way the splicing algorithm works (described below), I elected to store the representations, not in traditional binary, but in Gray Code. This has the advtange that numerically successive genes differ only by one bit, and so similarly sized numbers appear similar. In traditionally binary, changing by even one unit in each any direction can massively change the 'structure' of a number. (As a worse case example; moving from 127 to 128 in 8-bit notation inverts every single digit!). Gray Code is pretty neat and there are some novel uses. I encourage you to check out the Wikipedia article referenced above. [/GEEK ALERT]
Randomly selected initial values do not look pretty. (Well, they do actually look pretty in an abstract art context, but for this exercise, they do not look like me). Below is an initial plot of 32 rectangles of random size and random colour values.

What is next needed is a Scoring function that mathematically rates each creation. For this I simply summed up the simple errors (absoloute difference between the colour of each pixel in the source and the colour in this image). If I had used a more sophisticated error function (such as summing the squares of the differences), possibly convergence may have occured quicker as the very further away solutions would be penalized more severely, but I'm not entirely convinced as the process for selecting which chromosomes to keep in the pool (more below) already casts out the poor chromosomes quite well.
The algorithm
I initiated the algorithm by generating ten totally random chromosomes and placing these in a pool.
On each iteration, I kill off two of the chromosomes in the pool to make room for the next generation of off-spring. In true Darwinian style, only the strongest survive. On each iteration, the two weakest chromosomes are deleted.
Next, breeding occurs. Here, I take two chromosomes, cross-pollinate them to generate two new children, and return the parents and the two new off-spring into the pool. Initially I select just the two strongest chromosomes to breed-together, but I did not want to want to fast-track myself into a locally optimal solution and miss out on a globally optimal one; An operational researchers nightmare, the classic "I'm on top of a hill in the fog and there is nowhere 'up' from here, but I'm still not on top of the highest mountain in the area." Instead
In an effort to avoid being stuck in a locally optimal, but not globally optimal, solution I select the two chrosomoses that will procreate in the pool at random.
Finally, Mutation occurs. I select one chromosome at random from the pool, chose one random bit from this entity, and flip it! This mirrors mutation in nature; changes that just happen for no reason. This keeps the pool fresh by the introduction of new ideas that could improve the solution.
Cross-Pollination
To cross-pollinate, after the two parent chromosomes are selected, a random point inside the gene is selected. The two chromomes are then switched, downstream of this pivot point to form two new children. The first has the head of Parent 1 and the tail of Parent 2 and the second has the head of Parent 2 and the tail of Parent 1

A few thousand iterations later
After a few minutes, and a few thousand iterations, things have settled down a little. If you squint really hard you can convince yourself that some progress is being made. The colours are ligthening up and we've lost the black background. My shoulder on the left of the image has appeared, and you can make out the contrast between the right and left side of my face. The cards I am holding in my hand have appeared.


A few more iterations later


Getting Closer


The results
After a few hundred thousand iterations, I decided to stop. Here is the result along side the original image.


If you squint at it (go on, try it), it looks a little like me! Not bad for 32 random rectangles and a few lines of code!
