Motion Camouflage

Staying alive is pretty important.

Staying alive long enough allows an entity to procreate and spread its genes. This is what life is all about.

Crucial to staying alive is getting enough to eat. Some animals are herbivores, but carnivores and omnivores like to eat other animals. In this situation, there are predators (hunters), and prey (victims). The hunter’s goal is to capture the prey, and this can be through superior speed or strength, but it can also be through the application of stealth. A crafty predator can sneak up on her prey, reducing the distance to her target. The closer she can get without being detected, the shorter the final sprint needed.

The prey uses different senses to stay alert (and, hopefully, alive), including smell, sound, vision.

Vision will be the subject of this article.

Mammal eyes are complex, with lenses to focus light, muscles to move them, and cells that decode the light that they capture. Most mammals eyes have two basic kinds of detector cells (photoreceptors); rods and cones. Rods detect light, and cones interpret color. These photoreceptors are distributed with varying densities around the inside of the eye. Predators higher up the food chain (such as humans) have steerable eyes, both facing forward. This gives us binocular vision and the ability to judge depth because each eye has a different perspective on the same scene from a different position (stereopsis). Our eyes have a great concentration of cells in a sweet spot of the retina to give us crisp hi-fidelity images directly where we are looking. Around the periphery, we have much poorer resolution, but we’re very good at picking up motion (something moving to our sides), which we can react to, even though we can’t clearly see what it is. This is important because, as a human, when looking forward, our vision only gives us an approx. 120° cone of visibility. The part of the human eye that can distinguish fine detail, called the macula has a cone of just 6-7°

Cows have eyes on the sides of their heads; not facing forward. They have mainly monocular vision (each eye sees a different image with only a slight overlap at the front). They cannot compare the images to determine depth anywhere but directly in front of the their faces. They do, however, have an impressive 330° view of their surroundings, so they have the potential to detect a predator from most angles. This is called panoramic vision; a cow can see most directions without turning its head.

Interestingly, a cow walking parallel to a fence line might not even appreciate that it has walked past an open gate because it is facing forward and the view from the side eye does not portray depth and that there was a gap there. They can, however, detect motion in the panorama, and this is what they (and other prey) leverage to help stay alive.

Trees don’t move much, neither do walls, rocks, houses, cliffs, or things on the horizon. Tigers do move, as do other animals. To stay safe, a vulnerable animal is always on the lookout for movement. Movement is detected by a difference between images (a contrast or delta; something has changed). The stealthy hunter attempts to minimize their difference signal. This can be achieved by moving verrrryyyyy slooowwllly (all cat owners have witnessed this), or by using the environment around to hide or mask, and provide cover camouflage. There’s another interesting technique that can be applied and this is called motion camouflage. In motion camouflage, the hunter attempts to minimize the visible effects of his motion, and hopefully stays below the detection threshold of his prey.

Objects a long way away don’t appear to move much on the horizon when they move. Objects close to us move a lot. This phenomenon is called parallax. If you are a fan of classic arcade games, you’ll be familiar with the technique of scrolling horizontal banners at various speeds as an attempt to convey depth perspective. This technique is called parallax scrolling.

A tiger walking infront of a clump of trees will broadcast its movement because of the relative speed of it against the background; it will stand out.

If a hunter could advance on his prey and minimize the difference between what was seen by the prey against the background, it would give him the best chance of creeping up, undetected, against his victim. This is motion camouflage; attempting to hide by reducing the relative motion perceived.

Let's look at an example of a hunter trying to spear a goat. He is standing inbetween the goat and some background (say a clump of trees). From the point of view of the goat, if it were looking closely, it would see the image on the left. If the hunter were not moving, the goat might not detect his presence.

If the goat stayed in the same location, and the hunter was able to advance along a straight path between them then, relative to the background, the hunter would not appear to move side-to-side (not creating a lot of movement), but instead every so slightly, and subtly, 'loom' forward. If performed sufficiently slowly, this looming motion might go unoticed.

In real life, however, things are not usually that simple. The prey will probably be moving, and so the 'line' connecting the points will change. Let's break out a little math to see how this changes things. We'll define a coordinate frame with the original at the background point O, the Hunter H starting at coords (x_H, y_H), and the Prey P starting at (x_P, y_P).

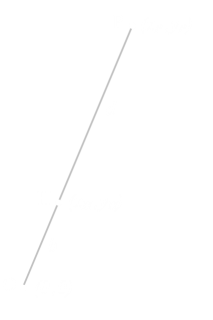
The distance between the hunter and the tree is b, and the distance between the hunter and the goat is d.

If the goat is moving, the hunter has to be clever. The path he follows is called a pursuit curve. (It is also sometimes called a scopodrome [skopien = to observe, dromos = act of running].

If the hunter simply always ran towards the goat (something called a 'pure pursuit'), he would follow a curved path as the goat moved. The curve shape would depend on the relative speeds of the two entities. If you are a regular reader of my blog you will have heard me talk about these things in the past in reference to how missile guideance systems work (which talks about another kind of pursuit curve, that of proportional navigation), and a much older posting about how to hide from a monster on a train with a laser gun.

The curved path the hunter would follow in pure pursuit would move him relative to the trees and blow his stealth cover. He needs to be cleverer.

Let's look at the path a clever hunter would take. The prey might not be moving on a constant heading, nor with constant speed, so let's just take a small time slice ΔT. In this time, the Prey will have moved from P to P', and we'll call the distance it moved S_P.

In the same time, the hunter can move anywhere within a circle of radius S_H. The ratio of the two distances S_H/S_P is the same as the ratio of the relative speeds of motion of the two entities. As we are looking for an optimal pursuit, we'll assume the hunter moves as far as possible in the time segment, and this means he can move to anywhere on the circle shown. Where the circle intersects the line from P' to O, is the place where the hunter will not appear to move side-to-side from the perspective of the goat.

If you look closely, you will see there are two solutions: H'₁ and H'₂. The first is the pursuit, solution and allows the hunter to get nearer the goat whilst minimizing perceived movement. The second solution shows a retreat path, and is the path the hunter show follow to get away without being noticed (oh how the tables have turned!)

Using the origin, we can define the angle to the goat P as θ, and the angle to the new positition on the goat P' as θ'.

Using the cosine rule, we can derive an equation for the triangle HOH' (where r is the new distance of the hunter from the origin):

And the the +/- gives us the two solutions we desire. We know θ', and now that we know r, we can determine where the hunter should move in the time step to stop side-to-side projection movement.

Looking at the equation (and the triangle in the diagram), it can be deduced that at certain relative speeds, depending on the current distance from the origin, it might not be possible for the hunter to remain in cover. If the difference in angles needed is too great, and the speed of the hunter too slow, the circle of all possible areas he is able to get to will not intersect the sightline.

Fans of the movie "The Hunt for Red October" (based on the book by Tom Clancy), might draw analogies to the "Crazy Ivan" maneuvers performed by Captain Ramius.

For the goat, his best strategy to detect potential prey is to make random jinxing turns (ideally at 90 degrees to the potential threat), in an attempt to pull any potential hunters out of motion camuflauge.

Here's a little app to experiment with. The red dots show the prey, randomly moving from left to right. Pressing reset generates a new random path. The 'tree' background is depecicted by the green dot in the lower left, and the hunter path is show in blue. You can configure the relative speed of the hunter to the prey and how granular the time steps are. If the hunter is able to catch the prey, the prey dot changes colour.

The above calculation shows how to minimize relative motion with the aim of staying hidden. Sometimes we want the exact opposite! Imagine you are riding a bike on the road. In the interests of staying alive you want to telegraph your presence as much as possible; wear high contrast clothing, use lights and, where safely possible, move on the road so as to maximize, your relative movement against a background to other road users.