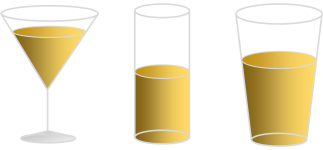
Glass Half Full?

There's a classic meme that periodically floats about the internet. It shows a partially filled glass of water* and asks the rheotirical question "Is the glass half-full, or half-empty?" The theory is that an optimist may be more likely to think of things as half-full, whilst a pessimist will look at the same glass and see it as half-empty. Personally, I'd don't think that it's a very useful physiological test. (Then, there is the joke answer that an engineer would not see it either of these ways, but instead, that you have the wrong sized glass!). However, it begs the question: How good are you at estimating when a glass is half-full?

*Beer, wine, coke …

If the glass you are looking at is cylindrical, then it's pretty easy to estimate the when the fluid is halfway. Using just your eyes, and dead reconning, most people can get to within a percent of halfway without breaking a sweat.

If you want to 'cheat', there are various ways to improve your answer: You could use a ruler on the side of the glass (or any blank piece of paper to which you can make a mark with a pen, then invert the paper and measure from the other end). You could mark the glass with a felt marker, then cover the top with coaster and invert it. If the seal holds you will be able to see if the fluid level in the inverted glass passes the mark (it's over half-full), is on the mark, or falls below the mark. If you don't have a drinks coaster, and are careful, you can slowly tilt the glass and see if you can get the meniscus to just touch the bottom rim at the top of the glass, and just touch the top at the bottom of the glass.

These simple techniques work well with a cylinder, but with a more complex shape we have to revert back to gut feeling. How good do you think you are? Let's try it out.

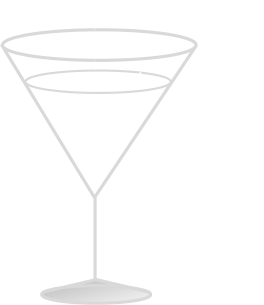
Below is a simple martini cocktail glass. It's nothing more than an inverted conical receptical.

How good do you think you are? Below are six glasses, viewed from the side. On the left is a glass that is filled to 40% height (as measured verticaly from the tip of the cone; 0% would be an empty glass, and 100% would be a a glass filled to the brim). Next is a glass at 50% height, then 60%, then 70%, then 80%, and finally 90%. Which glass do you think is closest to holding half the volume of fluid of a glass filled to the rim?

When you have your guess, click reveal to show the answer

Did that result surprise you? Yes, the closest to 50% volume is the glass that is filled to 80% height. In fact, to get to half volume, with any regular conical glass, you need to fill the fluid up to 79.37% height.

What is going on? How does that make sense? Looking at the side of the glass fools your eye, and your brain tries to estimate the area of the triangles and at what point the area of the triangle is approximately the same 'size' as the trapezoidal gap left at the top. This is totally wrong because the glass is in three dimensions! A cone gets wider as you get higher up the glass and the volume of the truncated cone at the top (officially called a frustum), scales in all dimensions.

What's also surprising is that a martini glass fileld up 'half-way' (to 50% fluid height), holds only 12.5% of the volume of a full glass! You probably guessed 70%, which is still only about a third of a full glass.

This is the variant of the classic cube-square principal. When you scale something up linearly, you have to scale all dimensions. If you have a cube of side one unit length, and double to size of the cube, it is now cube with sides of two units. However, the surface area has grown four fold (2×2), and the volume has grown eight fold (2×2×2).

This principal has massive consequences in all aspects of science. In engineering, it means that the mass of an object grows faster than its cross sectional surface area, so as a structure (such as a building), grows in scale, there is a more stress at the bottom eventually limiting how large it can be scaled. In biology, there are similar limitations to the diameter of bones and the flesh weight they have to support (there's a reason why an elephant looks like it does, and not like a scaled up mouse). There's also the issue of heat disipation and not being able to get sufficient surface area to radiate it away on larger mammals. For these reasons, it's clear that giant monsters in classic sci-fi movies such as Godzilla and King Kong are totally infeasible.

The cube-square law is not all bad news. Scaling up a hot air balloon makes it much more efficient. You grow more volume inside a scaled up balloon (providing the buoyancy/lift) faster than the surface area grows (which disapates the heat). A larger pan of soup stays warmer longer than two smaller pans. Catalysts that are ground up finer have more surface area per mass and react more efficiently (simiarly, finely ground gunpoweder burns faster than coarse powder).

Imagine the fluid in the glass as a frozen cone. To get to twice the volume we only need to scale up the length of a each side by ³√2, the cube root of two, as ³√2 × ³√2 × ³√2 = 2.

Let's prove it.

In the diagram below is a martini glass, normalised to a height of one unit.

The equation for the volume of a cone is:

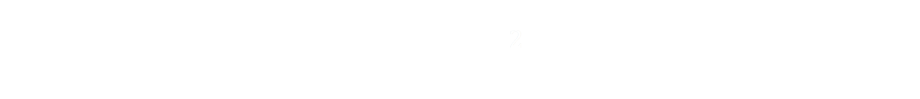
At a height of fluid h, the volume is therefore:

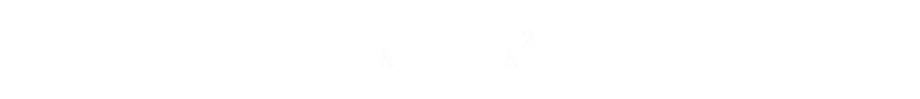
The ratio of the volumes from a full glass V₁ to a half-full glass is two.

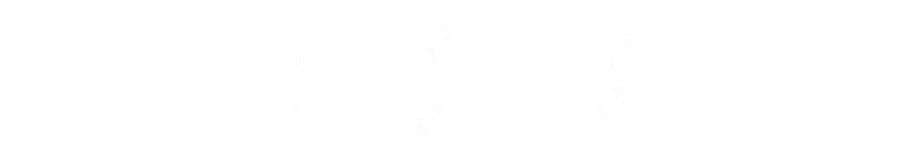
Finally, we know that the radius of the cone changes linearly with height and there is simple ratio relating the radious to the height (think similar triangles).

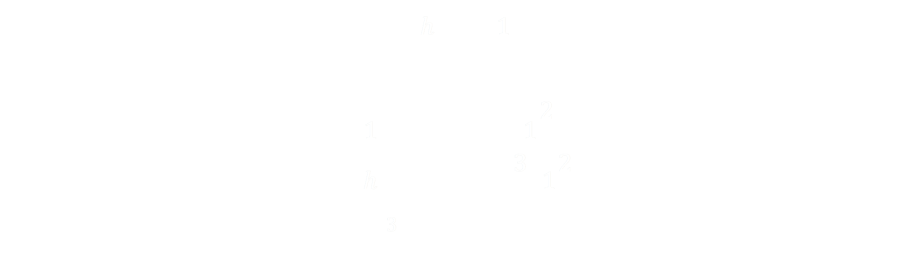
This confirms the result of 79.37%

Below is a little applet that shows this. Using your mouse, or finger, you can drag the fluid level up and down the glass and see the realtionship between the height and the volume.

Another common type of glass is the classic beer glass. This is also a frustum. It is a flat bottomed truncated cone.

The math here is just a little more complex because there are two variables (the radii at the top and bottom). Below is another app that allows you to experience how the half volume location changes with the radius at the top and bottom. The two sliders at the top allow you to change the diameters of the glass (the height remains fixed, nominally at one unit), and sliding up and down the glass changes the fluid level. The red line shows where the 50% point is. Note, it's possible to make the top narrower than the bottom, to make a flask. In this configuration, the 50% level is 'below' halfway.

There are lessons here: If you want to be a scrooge with your booze, serve your guests with small glasses. Half-size glasses hold only an eighth of the quantity of alcohol to full-sized glasses. At the other end of the scale, watch out if your host serves you drinks in extra large containers; twice the size of glass, and you're going to imbide eight times the volume!