Uncut Spaghetti
The article for this week comes from an excellent site I’ve discovered called MathPickle which contains dozens of projects designed to inspire, educate, and challenge, students and young mathematicians. I can’t remember how I first ran into this site. I think it might have been from following a link in a Numberphile video.

The problem
Start with a ‘dinner plate’ which is a square grid of numerically ascending numbers.
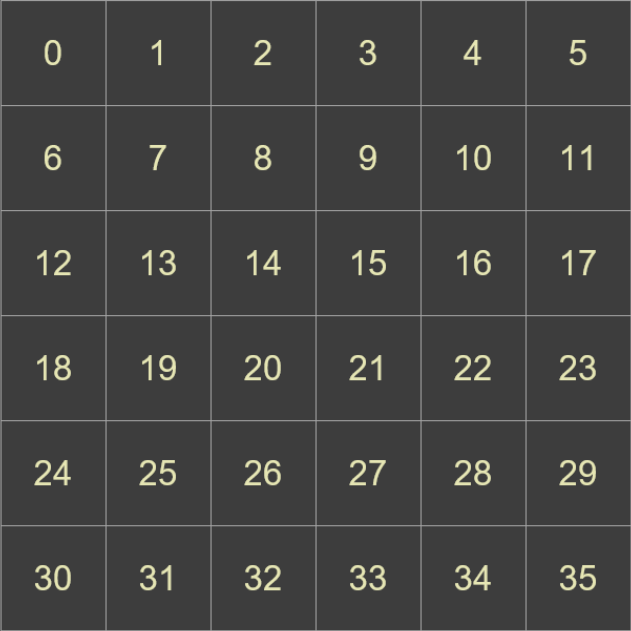
Select any of the numbers, for instance 19, as a starting location.
Look at the four cardinal numbers touching this square (in this case 13,18,20,25) and select the smallest of these (13) and move to that square, connecting it with a ‘spaghettum’ (a word made up by the puzzle author to represent the singular of spaghetti).
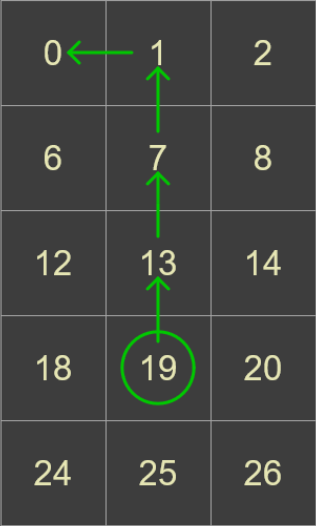
Repeat the process, each time, selecting the smallest number that has not been visited before, winding the spaghettum from square to square, like a piece of thread. Next to 7, then 1, then 0 …
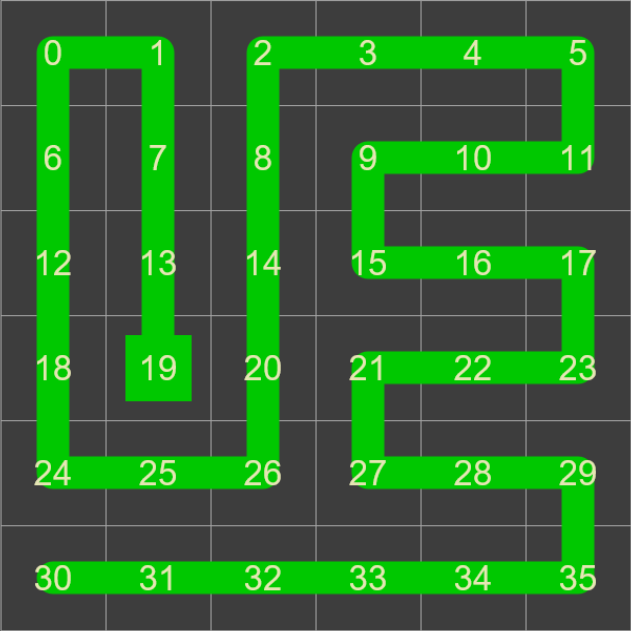
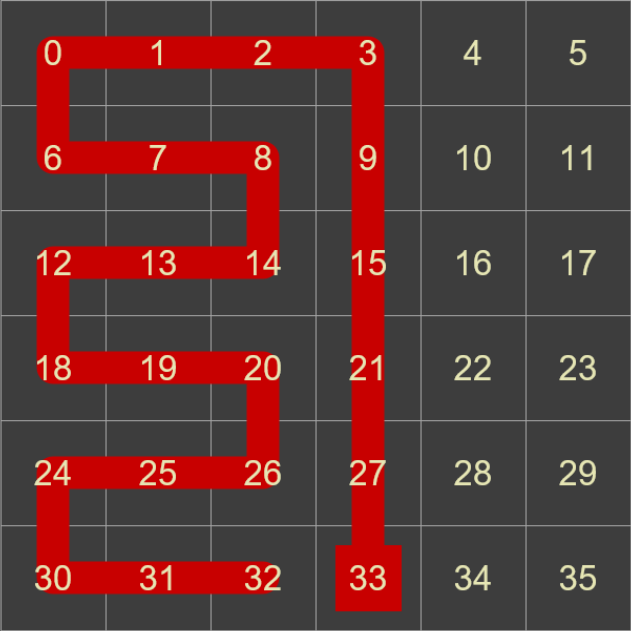
One of two things will happen; you’ll either successfully finish after having visited each square on the grid (shown green below, starting from square 19), or you’ll reach a dead-end and no further progress is possible (shown as the red snake example from square 33).
Advertisement:
All solutions
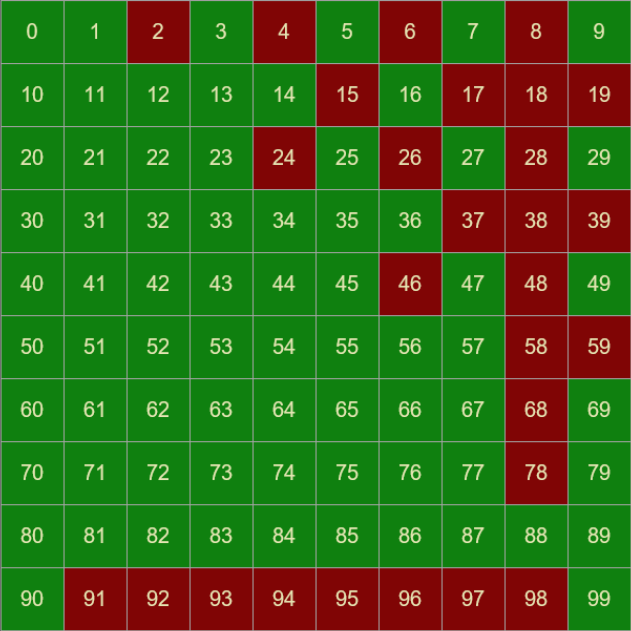
Using green to signify where a solution is possible from that starting location, and red where it is not, we can shade the grid to show which of the possible starting locations give perfect solutions. Here is the solution grid for a 6×6 sized plate:
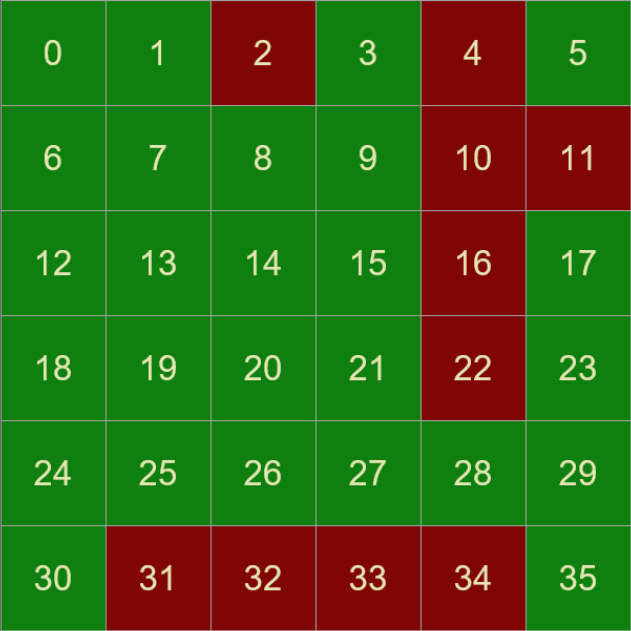
The pattern is interesting, and a little experimentation can show why some squares work, and why some don’t.
Different sized grids
Here are the solution grids for a few different sizes of starting plates.

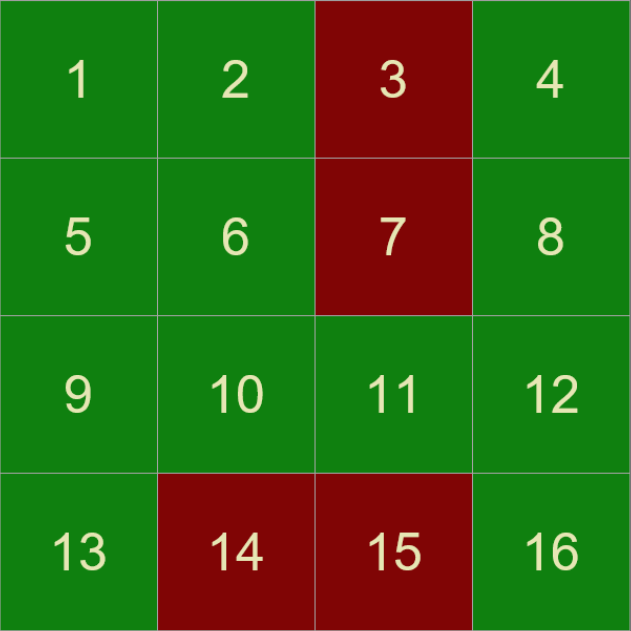
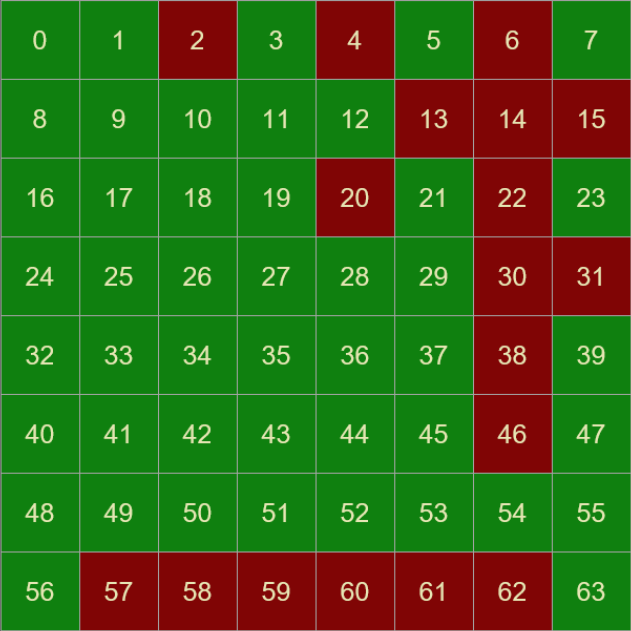
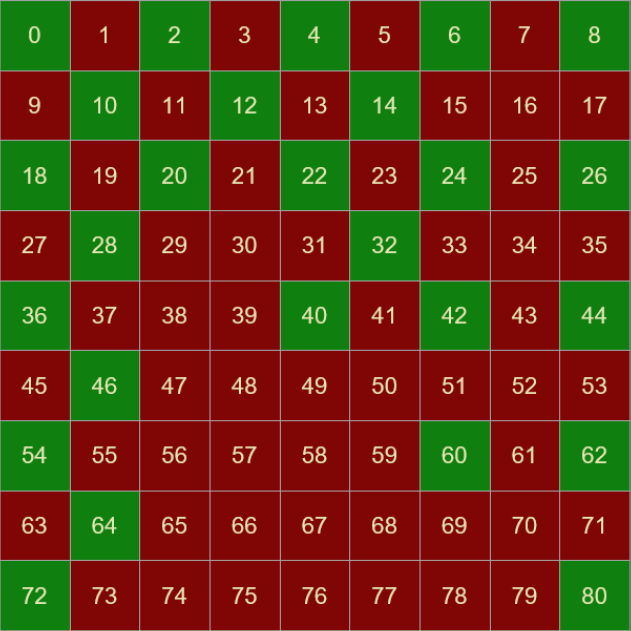
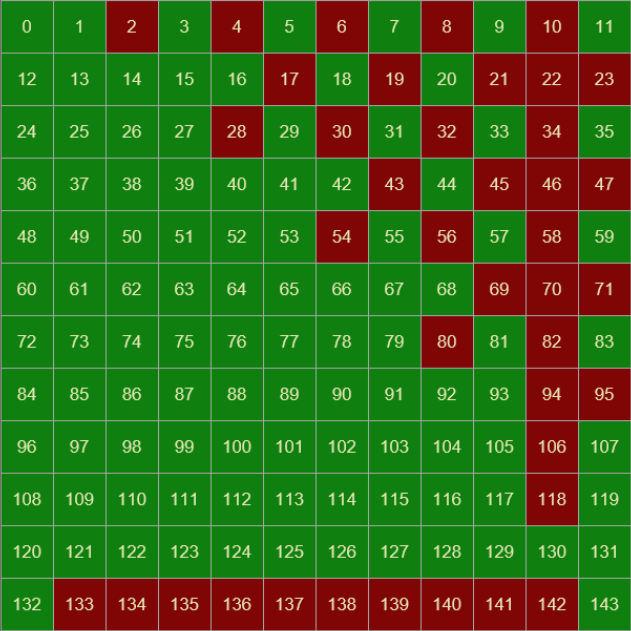
Even sized grids have many more starting squares with solutions. As you look at different sized grids (see app below), you will see patterns develop in the odd and even grids as their sizes increase.
This should not be a surprise as we discovered, on the article about self avoiding walks, that when we start from every-other space on a odd numbered board, it is impossible to make any complete path (nevermind an uncut spaghettum path). Before we even start, there is a checkerboard of impossible starting locations on an odd sized square grid.
Perfect Solutions
Does any size grid have perfect solutions from every starting square (all green)?
No, using the systemetric labeling system, it is not.
However, if we remove the restriction that the grid needs to be labeled consecutively, it’s possible to come up with patterns that are solvable from any starting location. Here are three of the (many) possible perfect configurations for a 4×4 board. Every square on these grids results in a perfect length path.

I generated these grids purely at random by inserting each number, then testing if it resulted in a perfect result.
The MathPickle page shows a solution for an 8×8. This particular solution has beautiful symmetry (trace the numbers around to see the pattern).

Try it out yourself
Here’s a little applet that allows you to experiment with the puzzle.
The buttons on the top allow you to adjust the grid size, and then clicking on any square of the grid shows the path of the spaghettum from that location.
On the second row are buttons to turn on/off the labeling of the grid, randomize the numbers, toggle if all solutions are show, toggle between rendering spaghetti as snakes or arrows, select if the lowest number on the grid is zero or one (to keep the software engineers happy), and finally a reset button (if the app is currently set in random mode, hitting reset will re-shuffle the grid numbers).
Hilbert Curves
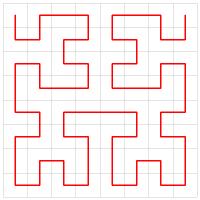
Another interesting, and related, topic are things called space-filing curves. The most famous of these goes by the name of the Hilbert Curve (named after the the German mathematician David Hilbert). Not only are Hilbert Curves continuous and space-filing, they are also fractal and self-similar. If you zoom in and look closely at a section of a higher-order curve, the pattern you see looks just the same as itself.
Hilbert Curve's have many interesting properties.
