Random points in a sphere
Let’s say you have a line of unit length, and want to find random points along it. You can do this by using a random number generator of range [0-1], and select points corresponding to the values you get. With a good random number generator, the points selected will be fairly uniformly distributed over the line.
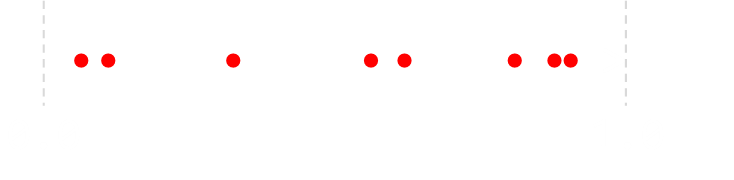
If we move into two dimensions, and have a unit square, how can we find uniformly distributed points in this square. The answer is fairly obvious: we generate two random numbers, one for the x-axis, and one for the y-axis. The points we get are uniformly distributed over the area.
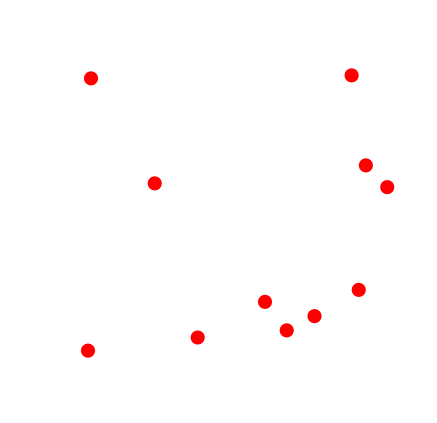
Scaling up to three dimensions, if we use three random numbers (for x,y,z components), we can generate random points uniformly distributed throughout the cube.
The question is, how can we generate points that are uniformly distributed inside a sphere?
How can we generate points that are uniformly distributed inside a sphere?
Sphere
The first, potentially naïve?, idea would be to enclose the sphere inside a bounding cube, select random points inside the cube, then discard points that fall outside the sphere. Let's take a look at this idea.
Below is a simple animation showing the concept. If you look closely, the points that are inside the sphere are coloured white, and those that fall outside the sphere are coloured red (Using the buttons at the bottom, you can toggle if the cube is show, adjust the density of points shown to one of three levels: Low, Med, High, and toggle if you want to allow your finger/mouse to rotate the shape).
Surprinsgly, this alogrithm works very well. But how many points are we 'throwing away'?
To simplify the math, rather than using a 'unit cube' (a cube with edge length one unit), we'll use an a cube with the origin in the center, and sides of length two units (going from -1 to +1). This is because we're going to use the cube to box a sphere with radius of one unit. (This type of cube is sometimes called an "eight cube" because it is comprised of eight unit cubes).
The volume of the cube is (2×2×2) = 8 units3.
The volume of the sphere that just fits inside this box (has a radius of one unit) is:
The ratio of the two volumes (sphere/cube) is therefore π/6 ≈ 52.4%

Just over half the points are inside both the sphere and the cube, so we're throwing away ≈ 47.6%
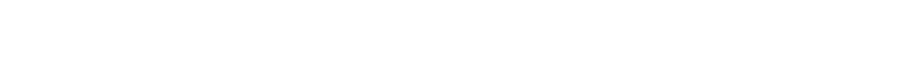
while (true) {
x = random(-1,1);
y = random(-1,1);
z = random(-1,1);
if ( sqrt( (x*x) + (y*y) + (z*z) ) < 1 ) break;
}
So, by generating random numbers from -1 to 1, and testing this inequality (which is the formula for a solid sphere), we can determine which points are inside, and which are outside (discard). We'll, on average, be generating about twice as many coordinates are we need and discarding about half.
Can we do better?
Normalize
One possible idea is to normalize and scale the point to force it to be inside the sphere. We can do this with a little bit of vector mathematics. Given a randomly generated point (x,y,z), there is a vector from the origin to this point. The magnitude (length) of this vector is √(x2 + y2 + z2), and if we scale the vector so that the magnitude is 1.0, by definition, it will be pointing to a place on the spherical shell. Once we know we have a vector from the origin to a location on the sphere, if we then scale this vector by a randon number from [0-1], we will select a point randomly along this length (somewhere inside the sphere).
Doing this means we don't have to discard any points, and we are using all the random (x,y,z) coorindates we generate (though we have to call the random function four times, not three). How does it do?
Well, at first blush it looks OK and all the selected points are certainly inside the sphere, but if we look carefully we'll see that the points generated are not distributed uniformly, and there are patterns in the points.
x = random(-1,1);
y = random(-1,1);
z = random(-1,1);
mag = sqrt( (x*x) + (y*y) + (z*z) );
d = random(0,1) / mag;
x *= d;
y *= d;
z *= d;
Using the app below you can look at the results of these algorithms. In the app below, the first button 'Disc', generates points using the discarding algorithm. The second button, 'Norm', generates the points based on the normalisation method. (Ignore that 'Pol#1' and 'Pol#2' for now, we'll talk about those later).
The above animation is a mobile friendly size. If your are running on a desktop, with a wider diplay, you can try this version (a larger version of the same thing).
If you look closely at the dot cloud generated by the normalization algorithm, you will see what looks like an eight pointed star, aligned at a bias, inside the sphere, what is going on?
Well, this algorithm is biased. If you recall back to the points that are outside the sphere, you will see there is more space at the corners, so this is more represented than the locations which touch the sides of the cube (The vector, that we scale, is longer when it goes to these corner regions than the face edges).
Clearly, this is not the way to go. Let's look at an alternative mechanism …
Advertisement:
Polar Coordinates
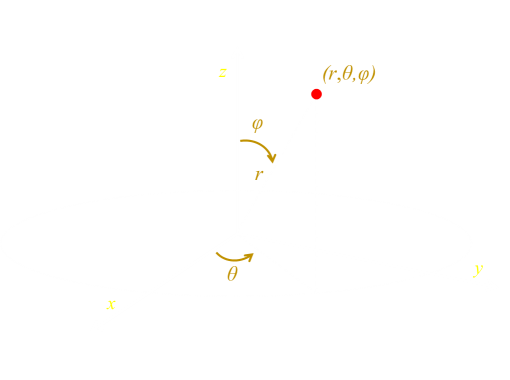
There are many alternative ways of describing the location of a point from the origin other than the cartesian (x, y, z). One of these is to use spherical polar coordinates. (r, θ, φ). In this coordinate system, r is called the Radial Distance, θ the Azimuth Angle, and φ the Polar Angle. The latter two angles are a little like Longitude and Latitude measurements on the Earth (but on the Earth the convention is to measure latitude as an angle 'up' from the Equator, instead of 'down' from the pole).
Using this coordinate system, aother possible way to generate random points inside a sphere is to select random values in this spherical domain. By selecting r in the range [0-1], we can ensure that the selected point is inside the sphere, great! Second by selecting θ in the range [0-2π], and φ in the range [0-π], we can scatter the points 'evenly' over this mesh:
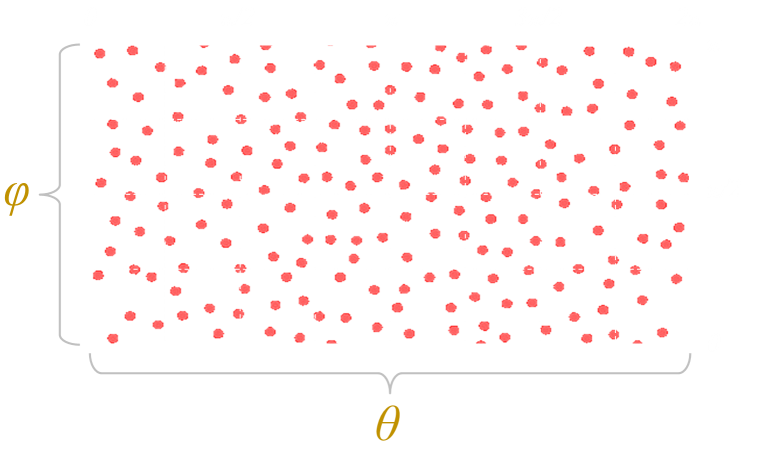
Here is code that generates points using this system (and then converts them back to (x,y,z) for rendering).
theta = random(0,TWO_PI);
phi = random(0,PI);
r = random(0,1);
x = r * sin(phi) * cos(theta);
y = r * sin(phi) * sin(theta);
z = r * cos(phi);
You can see the results of this in the app above, by pressing the "Pol#1" button.
Can you see there is problem? The dot cloud is not uniformly distributed and looks to cluster close to the axis of rotation. What is causing this issue?
Well, if you think about it, the two angles, if the points are distruted uniformly, will favor the polar locations as the distribution mechanism we've selected would uniformly map points on a cylindrical bar, not a sphere!
There's a way to correct this (for more details, see this thread on Math Stack Exchange).
theta = random(0,TWO_PI);
v = random(0,1);
phi = acos((2*v)-1);
r = pow(random(0,1), 1/3);
x= r * sin(phi) * cos(theta);
y= r * sin(phi) * sin(theta);
z= r * cos(phi);
This is shown in the app above using the 'Pol#2' button.
Another method
There's another commonly used method (I have no implemented it in the app), but this differs in that it uses a different random number distribution system. Up until now, we've used a uniform random number generator from which any number between the range is equally likely to be selected. If we have access to a function that generates random numbers with a normal distribution, then the following code will work (again see the Math Stack Exchange for details). Here the randn() function generates Gaussian distributed number with a mean of zero and a variance of one.
U = pow(random(0,1), 1/3);
x = randn();
y = randn();
z = randn();
mag = sqrt( (x*x) + (y*y) + (z*z) );
x= U * x / mag;
y= U * y / mag;
z= U * z / mag;
Results
The ironic part of this investion is that the initial algorithm (discarding points outside), which seems wasteful and not particulary elegant, turns out to be pretty good. Sure, about half the time we have to roll the dice again, but each of the the other techniques we've looked at requires more trips to the random function, more costly trig functions, or calls to a Gaussian random number function (which will probably be more computationally expensive).
#UBE Ugly But Effective
