Cutting a Square Cake
This article is about how to equally divide a square cake.
(If you had a round cake, and wanted to cut it into n-equal sized pieces, the answer is pretty simple; you can cut each piece into sectors with the appropriate same angle. Easy.)
What happens, however, if you have a square cake, like this delicious looking fruit cake?
How do you carve up this cake into equal sized ‘sectors’ (so that each cut goes to the center; we’ll see why this is important later)

Square Cake
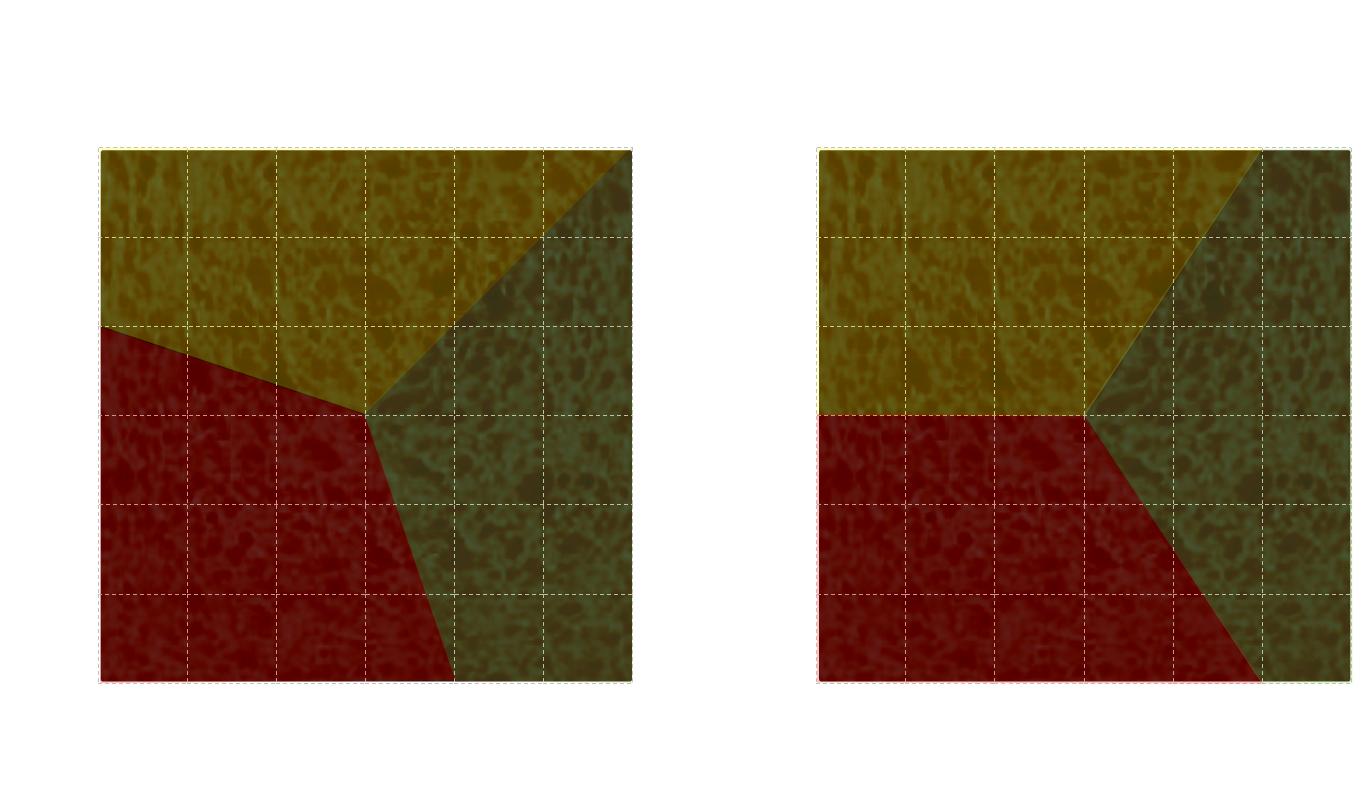
As an example, let’s say we have a square cake with each side of 6 inches, how can we cut this into three equal pieces?

Here’s an example of a couple of ways it can be done:

How did we generate these cuts? Well, the perimeter of the cake is 24”, and there are three pieces, so each piece will get 24/3=8” of perimeter. We start making our first cut to the center, then count around the perimeter 8”, make the next cut, then repeat. It’s as simple as that; divide the perimeter, make sure each piece has the same linear length, and cut to the center.
It doesn't matter if the perimeter goes around a corner, as long as there is contiguous 8" of perimeter for each piece. Because of this, there are an infinite number of continuous solutions depending on where there first cut is made.
A consequence of each piece having the same linear length of perimeter is, if the cake has icing around the sides edges, that each piece receives the same quantity of this icing. (If, instead, we cut the cake into three equal strips using two vertical straight cuts, the middle piece would be robbed of edge icing). Now you can see why it's important we cut to the center!
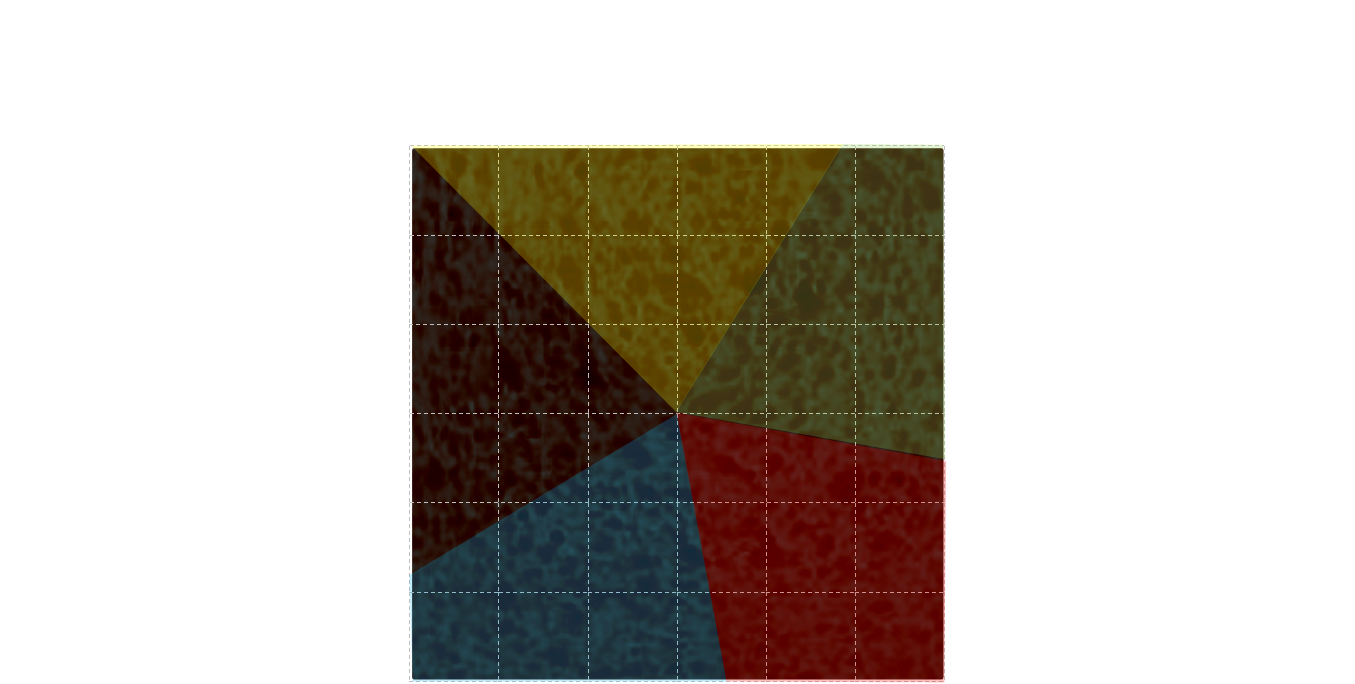
It does not matter how many pieces we need to generate. It's the same strategy. Here is how the cake would look if we had to cut it into five equal pieces. Here, the perimeter of each edge is 24/5=4.8”
The solution is simple and elegant.
Advertisement:
Why does this work?
This solution seems a little too easy. Why does it work?
Recalling back our geometry from school, the area of the triangle is half the base multiplied by the vertical height. In the diagram below, each of these triangles has the same area because they each have the same altitude and base.
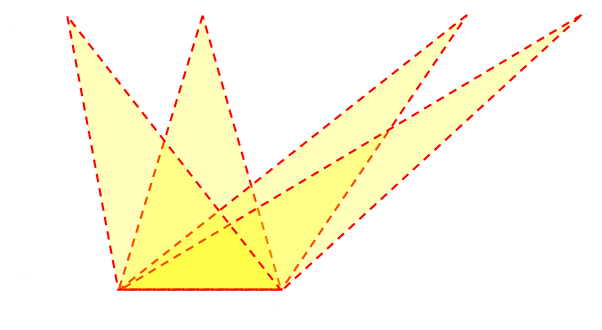
Imagine carving up the cake into lots of triangles, each with the same base (same distance around the perimeter). As you can see in the diagram below, each of the triangles A–D has the same altitude (their perpendicular distance from the edge to a line through the center is the same), and they have the same base. Each of the triangles A–D has the same area.
Similarly, you can see that triangles A and Z have the same area. In fact, as the square is a regular polygon, any triangle with with the same base on the edge, and a vertex at the center, will have the same area.
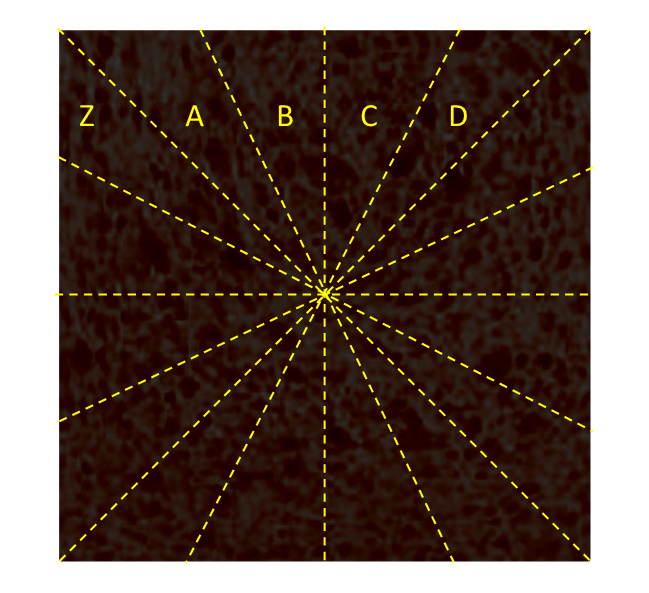
It does not even matter if a triangle 'wraps' around a corner. As the altitude is the same for both partial triangles, the area is simply proportional to the linear edge length.

Other Polygons
If you know a fancy baker who can make regular n-sided polygonal cakes, this strategy still holds. In a regular polygon, the perpendicular distance to each of the edges from the centroid is constant.

We can use our 'tape measure around the perimeter' strategy to fairly allocate a fancy cake!
(Taken to the limit you can see how this reduces to the same strategy that we use for a round cake, and how the internal angles are the same.)
Icing
If you can imagine scaling up and down the cake in size (based on the origin at the centroid), you can see that this method is agnostic as to the thickness of the icing (providing the icing is of uniform thickness all the way around). Each piece cut should get 1/nth share of the cake and side icing. (Subtract the difference between a cake with, and without, icing and the difference is just the icing).

OK, now I'm hungry …
