And the rockets’ red glare …
Today is the 4th of July, and in celebration, here are a few ramblings about aerial fireworks.
If you are in a patriotic frame of mind, there is a chance you might set off a few bottle-rockets (or larger), to get some bombs bursting in air. Bottle rockets have sticks on their sides and they are typically launched by placing the sticks inside a bottle (hence the name) to hold them prior to launching. If the rockets are larger, you might launch them from a tube. But what is the exact purpose of the stick? Many people think it is just to hold them during the launch and get them going in the right direction (and yes, this is true), but the primary function of the stick is to stabilize it in flight.
The stick of a bottle rocket is quite long, and this adds cross-sectional area. This moves something called the center of pressure of the rocket rearwards. The center of pressure of an object is, to aerodynamic forces, similar to what the center of gravity of an object is to weight. For a complex object, the center of gravity is the ‘average’ of all the weights of the individual parts. An object behaves as if it’s entire weight is acting through the center of gravity (more strictly speaking the ‘center of mass’), and forces can be resolved without any moments or twisting forces (You can balance on object on a pin if you place the pin at the center of gravity).
The center of pressure is the ‘average’ of all the aerodynamic forces acting on a body, and the entire lift being generated by the body can be modelled as if it is acting through that point.
For a rocket to be stable, the center of pressure of the craft needs to be aft of the center of gravity. In this way, if the rocket deviates, aerodynamic forces help push it back on course. It’s similar to a how a weathervane works on the top of a steeple. As the wind blows on a weathervane, because it is asymmetric in shape, the larger area of the ‘tail’ of the vane, points the ‘nose’ into wind. In a rocket, wind is not blowing onto it, it is being propelled forward but, relative to the rocket, it’s the same thing. This is called Weather Cocking
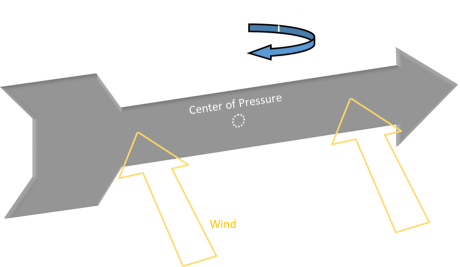
It’s this reason that you might sometimes see fins on the tails of rockets and missiles. These things add ‘area’ and help move the center of pressure aft to keep the rocket stable.
Interesting Facts
This science leads to two counterintuitive facts about rockets:
- When launched in a breeze, a rocket will turn into the wind and head upwind as it climbs into the sky. Most people think the wind will blow it downstream as it pushes on the side of the rocket, but what happens is that the rocket rotates around its center of mass, and the force of the side wind on the craft acts like a pushing force on the center of pressure; pivoting the nose into wind. As the speed of the rocket is faster than the wind, the resolve component moves the craft upwind. Remember this when launching your rockets on a windy night.
- The second counter intuitive fact is that if you want to make your rocket more stable you add more mass to the nose of the craft! More mass higher up shifts that center of gravity more forward, increasing the separation between the center of gravity and center of pressure. A greater distance means the length of the moment arm of the aerodynamic force is larger, meaning the correctional torque is higher. The difference between the CG and CP is given the name static margin. Again, this seems counterintuitive; most people think that you should add mass to the tail of the rocket to increase stability, sort of like a pendulum. This is not true.
NOTE: Simple aerodynamic stability is great for humble disposable rockets but, when you are dealing with larger commercial rockets, there are other tricks that can be employed. On commercial rockets, the entire engine and exhaust nozzles can be gimballed and steered to provide vectored thrust. This is used to both steer the craft and provide stability. Also smaller ‘vernier thrusters’ can be placed around the circumference of the vehicle, pointing outwards and downwards, and by adjusting the output of these tiny engines, stability and steering can be applied. It’s for these reasons that you don’t see big fins on modern launch vehicles.
For unguided missiles (such as firework rockets) you want a large static margin; they need to be stable, and predictable, and you don’t need to worry about maneuverability. A high static margin comes at a cost, and this is slow response to control inputs, poor maneuverability, and high forces need to change course. Guided missiles, which need twitchy response to chase a target, will have a low (or even negative) static margin. Computer controls can keep a negatively stable entity flying with constant micro adjustments like balancing a pencil upside down on your finger; the computer is constantly fighting to keep missile pointing in the right direction. The added advantage of this fly-by-wire stability is that, when a turn is needed, the aerodynamic forces want to turn you and help in the matter.
Advertisement:
Mortars and Shells
Simple stick stabilized rockets work out well for small pyrotechnics, but don’t scale well. If you want bigger bangs and larger bursts in the air you need to get more payload up there. A larger rocket, with a few pounds of excitement at the front end, would require a stick 20-30 feet in length; not very practical. Also not very safe. Launching a stick that big (and heavy) into the air, then having it come down who-knows-where (probably on fire), is a recipe for disaster. It’s also not efficient to carry all that mass up into the air that does nothing useful to the display.
The solution is that, above a certain size, aerial fireworks are mortars. These are spheres (sometimes cylinders) of bursting shells that are launched into the air from a mortar tube. The shells have an internal fuse that burns at a known rate to allow the shell to attain the desired altitude before igniting a bursting charge in their core. This bursting charge splits the shell open and ignites a plurality of stars inside the shell that burn in pretty ways. A shell is wrapper mainly in paper, and the vast majority of the shell either burns, or flits harmlessly through the air.
The shell is launched out of the tube using a lift charge which accelerates the projectile up the tube and into the air.
Image: marksfireworks.com
Spherical shells sitting on lift charges.
Image: five-guys-facts
A cross section of a large shell. The lift charge is seen at bottom. The vertical spine is a timed fuse that burns as the shell flies up on the air. At the center of the shell is a burst charge that explodes the shell. The round balls are called 'stars' and these burn slower, and with bright colours, to produce the characteristic look.
Image: fireworks-portal.gq
Three small mortar launch tubles with shells about to be inserted.Spheres in the sky
When aerial fireworks explode, they make beautiful spheres in the sky. If we imagine a blob being fired into the sky then exploding into hundreds of little pieces, each of these little pieces will leave the site of the explosion with the same velocity, but in a random direction. The distance they travel (from the original) will be the same in the same time, hence they burst into a sphere. Superimposed on this is the inevitable pull of gravity and if you look closely at the individual paths of the stars inside the bursting shell, you will see it is made up of a collection of glowing parabolae*.
Image: adzla
Timing
The goal of the fireworks designer is to get the shell sufficiently high into the air that it can safely explode, and also so that the full sphere of the explosion is visible to the audience. The bigger the shell, the higher it needs to go, so the faster it needs to leave the ground. Ideally the shell will burst at its apogee (the highest point it obtains from the Earth). Bursting too soon, or too late, has wasted lift charge getting it up there, plus could be potentially dangerous if it explodes too close to the ground.
Ballistics
A mortar shell follows a pure ballistic trajectory. It is not powered in flight. All the energy is added in the launch tube, and it departs the Earth at full speed, slowing down as it trades kinetic energy for potential energy (height). If we ignore drag (wind resistance) we can do some simple calculations.
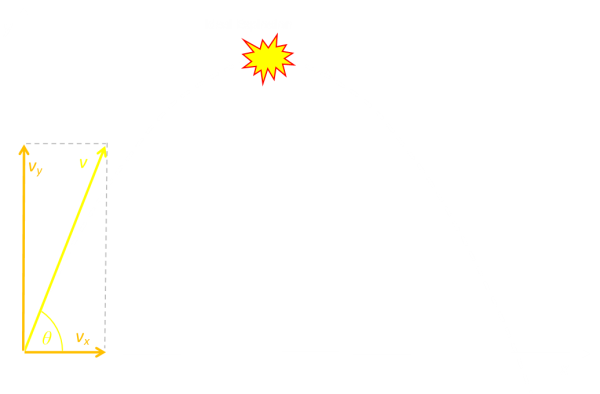
At firework shows, most mortars are aligned close to vertical to turn as much of the energy as possible into going straight up. But let’s generalize and look at a ballistic trajectory where the launch is at an angle. We can look at the resolved velocity components and displacements in two directions: parallel to the Earth (x-axis), and perpendicular to the Earth (y-axis).
The velocities in the y-direction will be affected by gravity, those in the x-axis, not.
At apogee, the firework will be at peak altitude. This means its vertical component will be zero, and the time to reach this altitude is t
It’s altitude can be calculated as:
According to this table from pyroinnovations.com, here are a list of muzzle velocities for shells of various dimensions.
I’ve converted these into metric and used the equations above to calculate the flight time (in seconds), and what the altitude of the apogee would be. I’ve used the assumption that the mortar tube is pointed 85° to vertical.
| Caliber | fps | m/s | Flight Time (s) | Altitude (m) | |
|---|---|---|---|---|---|
| 2" | 117.5 | 35.8 | 3.6 | 65 | |
| 3" | 144.0 | 43.9 | 4.5 | 97 | |
| 4" | 166.0 | 50.6 | 5.1 | 129 | |
| 5" | 186.0 | 56.7 | 5.8 | 163 | |
| 6" | 203.5 | 62.0 | 6.3 | 195 | |
| 8" | 235.0 | 71.6 | 7.3 | 259 | |
| 10" | 263.0 | 80.2 | 8.1 | 325 | |
| 12" | 287.5 | 87.6 | 8.9 | 388 | |
| 24" | 393.0 | 119.8 | 12.2 | 725 | |
| 36" | 481.0 | 146.6 | 14.9 | 1087 | |
| 36" | 533.2 | 162.5 | 16.6 | 1335 |
For large shells, that's quite a long time to loft it to the correct altitude. You can begin to appreciate the art of coordinating explosions to a musical sound track for a public display. (And also, remember that sound takes a while to reach the audience so you also need to take into account the distance between where the firework will burst and where the majority of the crowd will be located. Because of the height component, this will not be as simple as the distance on the ground).
World’s Largest
According to Guinness World Records, at the time of writing this article, the largest firework shell successfully launched was a 2,797 pound behemoth (1,269 Kg); that’s more than car!
It was 62” in diameter, was launched from a 26 ft long metal pipe buried into Emerald Mountain in Colorado, and with reported muzzle velocity of around 300 mph. Below is a video of this epic event.
I watched the video and timed the duration between the launch boom and the explosion boom. I clocked it at around 16.5 seconds. Using the formula above this gives an approximate muzzle velocity of 162.5 m/s which is closer to 363.5 mph, and gives and apogee height of 1,335m which is around 0.83 miles. Imagine shooting a car 0.83 miles into the air!
*Parabola, or not
Strictly speaking, a firework (or any other object launched ballistically from the Earth) does not follow a parabolic path, but instead an elliptical one. It’s just that the ellipse in question has such a large major axis that, other than in extreme conditions, is indistinguishable from a parabola.
When you throw a baseball, you are actually launching the ball into orbit! The ball arcs away and, in accordance with Kepler’s laws, follows an elliptical trajectory with the center of mass of the Earth as one focus. However, the ball collides with the surface is it desperately tries to orbit around this center of mass and return to the point where it was launched. If you were able to replace the Earth with a black-hole-like point mass at the center of Earth, the ball would whip around it, in orbit, and come right back to where you threw it from!
The faster you throw the ball, the further it goes. If you could throw the ball fast enough, it would fall around the Earth, constantly, matching its curvature and be in orbit without colliding with the surface. It’s a meaningless question to ask “how high do you need to get to be in orbit”, the question is “how fast do you need to go to get into orbit”! (The answer, for the Earth, is around 7,910 m/s or 17,692 mph – that’s just short of 5 miles per second! If you are interested, the orbital velocity is 1/√2 times the escape velocity of planet).
That's quite fast! Comparing this to the muzzle velocities of shells you can see why, when we launch payloads into space, we send them up on powered rockets and don't attempt to ballistically slingshot them into orbit. The acceleration needed to move a payload from rest to thousands of miles an hour (even if we had a very, very long launch tube), is just crushing!