AB or BA
A simple question this week. Given two real numbers: A and B, which generates the larger number? AB or BA ?
Is AB > BA or BA > AB ?
Is it better to use the larger number as the base or the exponent? It seems such a trivial thing, even if we’re not sure, how hard can it be to test a few examples?
- With A=4, B=5 then 45 =1,024 and 54= 625. This seems to indicate that using the larger of the two number as the exponent gives the largest result.
- This is confirmed with the set {2,7}, where 27 = 128 cf 72 = 49. Again using the larger number as the exponent maximizes the result.
- Hold on though, what about {1,7}, here 71 = 7 , which is larger than 17 = 1. Here we get a larger result with the smaller number on the exponent.
- Similarly with {2,3}. Here 23 = 8, which is smaller than 32 = 9, so it appears that sometimes putting the bigger number in the exponent does not result the largest result. What gives?
- Then there is a seemingly arbitrary flip-flop. Take the set {1.6, 6.2} and compare this to pair {1.6, 6.3}
1.66.2 < 6.21.6 but 1.66.3 > 6.31.6
Somewhere in between {1.6,6.2–6.3} it flips over, and also somewhere {1.6–1.7,6.2}, so the transition point depends on both numbers.
Something is clearly going on. Want to experiment yourself to see if you can see a pattern?
Advertisement:
Try it out yourself
Below is a little app for you to be able to experiment looking for a pattern. Be careful, using powers, it’s pretty easy to cause overflows. You can also use negative numbers, but bear in mind that negative numbers with non-integer exponents are not defined.
Explanation
Did you find a pattern? It's not obvious.
Let’s assume that from the set {A,B} that the equality holds
We can raise both sides to the same power without affecting the inequality. Let’s raise each side by the power 1/(AB).
So we can see that the inequality holds if the xth root of x of one number is larger than the other.
Graph
Here's a graph of the function:
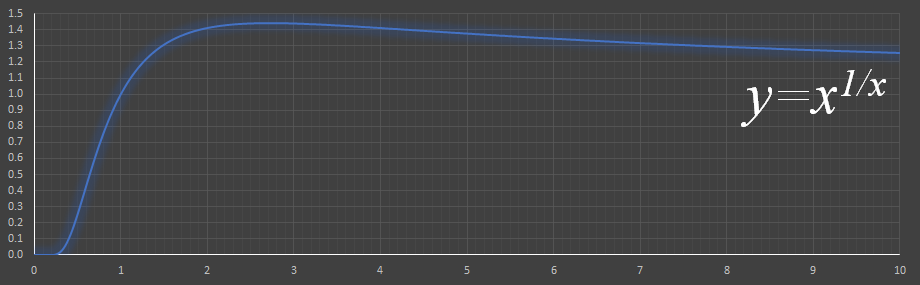
It's an interesting curve. Eventually it asymptotes to one.
To find out which number to put on the exponent, and which the base, simply look up both numbers on the x-axis and find their value on the curve. The number that represents the higher value when read on the y-axis is the number to put in the base.
We can use calculus to find the maximum value of the curve. (Differentiating and setting this to zero to find the turning point). This occurs when x=e.

This tells us all we need to know to answer the question.
- If both numbers are above e, then place the larger number in the exponent position.eg. {10,12} gives 1012 > 1210. The exponent demoniates.
- If both number are below e, then place the larger number in the base position. eg. {1.5,2.5} gives 2.51.5 > 1.52.5
- If one of the numbers is less than one, and the other above one, then the number less than one should always go in the exponent (the curve to the right is always higher). eg. {0.6,5} gives 50.6 > 0.65
- Otherwise, raise both numbers to the power of their reciprocal, and place the number with the largest result in the base. eg. {1.6,6.2} gives 6.21.6 > 1.66.2 (becasue 1.61/1.6 ≈ 1.31451 and 6.21/6.2 ≈ 1.342162)
- If one of the numbers is e then, as it's the peak of the curve, this will always be the base, and the other number will always be he exponent (regardless of it's value!) If you remember this trick, it's easy to answer the question: which is bigger eπ or πe?
Additional Trivia
We can use the curve above to answer questions about what pairs of numbers give the same result when raised to each others' power.
When x>1 then there is always a chiral value that completes the pair xy=yx.

For example 1.219.5763 = 19.57631.2
As regards integer solutions to xy=yx, there is only one, and this is 24=42.
