Social Distancing at the Park
Social distancing is really important. Covid is mainly spread by respiratory droplets. Anything you can do to reduce your exposure reduces your risk of infection (or transmission, if you are an active carrier). Barriers, such as masks and screens, help. Reducing the time of your exposure helps. Being outdoors helps (wind moves the droplets away, and being outside means there is no forced air-conditioning recycling the air). Physical separation also helps. Guidelines are that we should try to be at least 6 feet away from other people. We are, however, also humans, and not best suited to incarceration and self-confinement. It can be good to get out and, safely, consume some fresh air (and sunlight helps the body make Vitamin D, from cholesterol in our skin). If you can get out, safely, it’s beneficial to carefully get some exercise.
Many parks and authorities have, cleverly, tried to assist in the enabling of outdoor exposure whilst maintaining safety by providing guidance in social distancing. They have been doing this by using the devices they normally use to paint out tennis courts and baseball diamonds to mark a plurality of circles in their fields. The circles are appropriately spaced for social distancing, and I applaud their ingenuity. However, most of the images I’ve seen have the circles arranged in a non-optimal manner:
 Image: Marcella Winograd
Image: Marcella WinogradPlease don’t take this as a ding; I salute and admire their work, and it seems to be working great - well done! I’m looking at this from a purely engineering/mathematical angle.
I wrote about this topic a long time ago in 2014, in my article about optimal packing, but it’s worth a recap.
Optimal Packing
The pictures of the fields above are using a technique called Square Packing. Square packing looks very neat and organized with everything aligned in rows and columns, but is not the most efficient way for circles to tile a plane. In fact, it’s only 78.54% efficient. There are patches of wasted (unused) grass between the circles. The optimal way to pack circles on a flat plan is in arrangement called Hexagonal Packing. In Hexagonal packing, each alternate row is staggered half-way to one side, like bricks in a wall, and this allows it to nest-up close to the row above. The usage efficiency of hexagonal close pack is 90.69% - this is a big improvement.

Square Packing
Hexagonal Packing
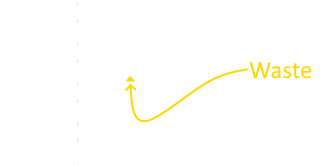
Another good way to think about this is how to optimally cut out disks of pastry from a rolled out sheet of dough and minimize the wastage on each roll.
 Image: Pete Harmer
Image: Pete HarmerAdvertisement:
Edge Effects
Optimal efficiency for hexagonal packing can only be theoretically obtained on an infinite plane. Most fields are rectangular in nature (and finite in size!), and so suffer edge effects. In a hexagonal pack, every other row has a half-gap at one end which is unused and reduces the efficiency. If the field is small, this can have an impact, but once the field gets above a certain size (relative to the size of the circles), the efficiency of the packing quickly dominates over the edge losses.
In the example below, here are two arrangements for 42 circles in the two difference packing formats. The area of the red rectangle on the right is less than the one of the left. Hexagonal packing is more efficient.

Further down the rabbit hole
There's an interesting study in mathematics, and this is to find out the most efficient way to pack n circles into a square.
For small numbers of circles, the results are obvious, have obvious symmetry, and have been mathematically proven to be the optimal. Above approximately twenty, however, the optimal answers have not been proven, or even known/confirmed. Currently known best solutions have been determined by various approximating algorithms (simulated annealing, and randomly 'jiggling' the circles whilst trying to reduce the wall widths like a trash compactor on the Death Star).
Below are solutions for the arrangements of the first twenty sets of circles. For each number of circles, I've shown just one of the layouts (there are trivial reflections and rotations for all the solutions), and sometimes canonical forms.
For each I've shown the packing efficiency η as a percentage, and the radius r that the circle would need to be to fit this configuration into a unit square.
If, instead, you want the size of the square that is needed to contain that number of unit-radius circles, simply take the reciprocal of radius value. (This is the solution to what is the smallest piece of square pastry you would need is order to be able to cut out n unit-radius circular pie crusts with the smallest amount of waste).
n=1

η=78.54% r=0.5000
n=2

η=53.90% r=0.2929
n=3

η=60.96% r=0.2543
n=4

η=78.54% r=0.2500
The first few solutions should surprise nobody. These all look the configurations we'd expect. When n=4 we can see the first (non-trivial) appearance of the square packing configuration.
n=5

η=67.38% r=0.2071
n=6
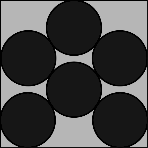
η=66.40% r=0.1877
n=7

η=66.93% r=0.1745
n=8

η=73.10% r=0.1705
The shape for n=6 might be a little of a surprise, and for n=7 there is a 'loose' circle that rattles around. Symmetry returns for n=8 and n=9, and n=10 almost looks random!
n=9

η=78.54% r=0.1667
n=10

η=69.00% r=0.1482
n=11

η=70.07% r=0.1424
n=12

η=73.85% r=0.1400
n=11 has a couple of loose circles, and though it look like a hexagonal packing, n=12 has bigger gaps between some adjacent circles. n=13 and n=14 also both have loose circles.
n=13

η=73.33% r=0.1340
n=14

η=73.57% r=0.1293
n=15

η=76.21% r=0.1272
n=16

η=78.54% r=0.1250
Square packing returns for n=16. Square packing is still the optimal for the next perfect squares of n=25 (5x5), and n=36 (6x6), but by the time we get to n=49 (7x7), it is no longer the optimal.
n=17

η=73.36% r=0.1172
n=18

η=75.47% r=0.1155
n=19

η=75.23% r= 0.1123
n=20

η=77.95% r= 0.1114
As mentioned above, hexagonal packing is, theoretically, the most efficient packing scheme, but suffers from edge effects. As the circles get smaller, and their number increases, these edge effects become less significantly. By n=49, a distorted square pack (squashed and sheared slightly towards a hexagonal packing is the most efficient packing) becomes more efficient. It's not very pretty, but it takes less space. At n increases, the patterns get closer to hexagonal packing.
n=49

n=64

n=81

n=144

The above images come from this (very excellent) web site of the current known optimal solutions.
Graph of Efficiency
Here is a graph of how the optimal efficiency changes with n:
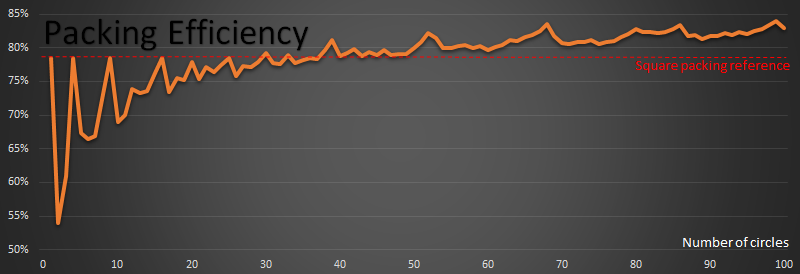
The red reference line shows the 78.54% percent that square packing achieves.
- For n=1,4,9,16,25 the packing on these perfect squares, by definition, meets the red line.
- From above, by the perfect square n=49 (7x7), we are already more efficient than square packing.
- The first time that a packing achieves a higher density than square packing is when n=30
- Past n=38, every packing efficiency is higher than square packing efficiency of 78.54%
- There are spikes at n=39, n=52, n=68, n=86 and n=99. These look very close to hexagonal packs when you look at them
Packing in three dimensions
The principles of packing circles into squares can be extended into three dimensions to cover the concept of packing spherical balls into cubic boxes.
As with 2D, the optimal packing for a single layer is a hexagonal arrangement, with each sphere being surrounded and touching six others in the plane.
On top of this, we can layer another carpet of hexagonal packed balls, aligned so that the centers of the new layer lay in the crotch of the layer below.
This will give us a 'two layer' cake. We can label the layers A and B to differentiate.
Ontop of these two layers, we have two choices. We can make our third layer be a duplicated of the first layer, so that the two layers alternate ABABAB, or we can make the third layer appear over the top of the void in the first layer that has not been covered yet. This three layer pattern then repeats ABCABC. These two variants are shown below:
Hexagonal Close Pack

ABABAB
Face Centered Close Pack

ABCABC
Both of these result in optimal packing (you can see there should be no difference between them, the C layer is just like the A layer, but rotated 180°). These structures are studied by chemists as they represent the arrangement of atoms in some crystalline elements.
The ABABAB format is given the name Hexagonal Close Packing, and the ABCABC format is given the name Face Centered Cubic Close Packing (reflecting the fact that the eight points on adjacent layers two apart make the corners of a 'cube' with an additional sphere in the middle).
In both arrangements, each sphere touches six spheres in the same layer, and three from the layer above, and three from the layer below. Every sphere touches twelve others.
The efficiency of a close packing is just over 74%
Hexagonal close pack is the structure seen in crystals of Be, Co, Mg, and Zn (and also He, if you get it really, really cold).
Face centered cubic (also called cubic close pack) is the structure see in elements such as Ag, Al, Au, Ca, Co, Cu, Ni, Pb, and Pt (also all the rare gasses, except He, if the temperature is lowered enough to make them solid).
Guess the number of bubble gums
If you look about, you'll see plenty of hexagonal close packing around you. If you tip marbles into a jar, they'll land into something like a hexagonal close pack.
A pyramid of stacked canon balls is stored as a hexagonal close pack.
 Image: Let Ideas Compete
Image: Let Ideas Compete
 Image: Nigel Munoz
Image: Nigel Munoz
Now that you know that hexagonal packing is approx 75% efficient, next time there is a 'guess the number of bubblegums in the machine' competition, knowing the diameter of the container, the diameter of a gumball, and a little high school math, you can make a much more educated guess. If you win, be sure to share.
Social Distancing at the bar
If you like this article, you might also like this article about social distancing at the bar and it’s relationship to Fibonacci Numbers.

Stay safe!
