Chess Tournament Puzzle
You have entered a chess tournament. You will play three games against two opponents.
One of your opponents is a strong player. You estimate your chances of winning any game against her at 30%.
One of your opponents is a weaker player. You estimate your chances of winning any game against him at 75%.
You must alternate which opponent play in each of the three games, but you can elect to choose which opponent you play first. You will win the tournament if you win any two games in a row. What is your strategy? Who should you play first?
You win the tournament if you win two games in a row

Strategy
This all comes down to the decision, should you elect to play weak-strong-weak, or strong-weak-strong?
Logic would seem to suggest that weak-strong-weak is the correct strategy because you are playing the weak player twice, and the strong player just once. You are much more likely to win your games against the weak player, so it’s best to maximize the number of times you are playing this opponent, right?
Actually, this is the wrong strategy!
This counterintuitive result is because the rules are that you need to win two games in a row to triumph in the tournament. By playing the weaker opponent in the middle it gives you two bites at the apple at defeating the stronger player (by winning game1 or game3); this outweighs the other way around in which you have only one chance to beat the stronger player. To convince yourself of this argument, take it to the extreme; imagine the game against the weaker player is a total gimme, and you win instantly. You can now see that putting this gimme in the middle gives you two chances against the strong player. We’ll look at the math in detail below, but first let’s examine all possible combinations of results. There are eight possible permutations of Wins and Losses (Assuming you play all three games). There are only three combinations that result in tournament conquest for you.
| Result | |
|---|---|
| Win-Win-Win | |
| Win-Win-Loss | |
| Win-Loss-Win | |
| Win-Loss-Loss | |
| Loss-Win-Win | |
| Loss-Win-Loss | |
| Loss-Loss-Win | |
| Loss-Loss-Loss |
Math
There are lots of different ways to look at this problem, but maybe the easiest is to only concentrate on the three possible victory scenarios: WWW, WWL, LWW. Actually, there are only really two paths we care about. If you win the first two games, it does not matter about the state of the third. It’s game over; you’ve won irrespective of the outcome! The only states we care about are WWx and LWW (either you win the first two games, or you lose the first and win the next two). Here’s this in stick diagram form:
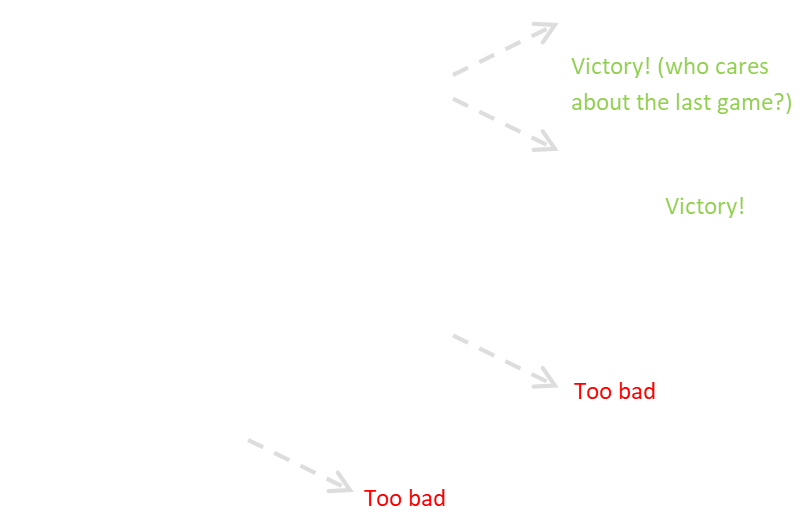
Let’s look at this generically. Let’s define the chance of winning the game against the strong player as s, and the weak player as k.
Advertisement:
Weak-Strong-Weak
If we get two wins to start off, probability ks, for a win against strong, then weak, we don’t care what happens next.
If we get a loss first against the weak player, probability (1-k), followed by a strong win, s, and a weak win k, the probability of this path is (1-k)sk.
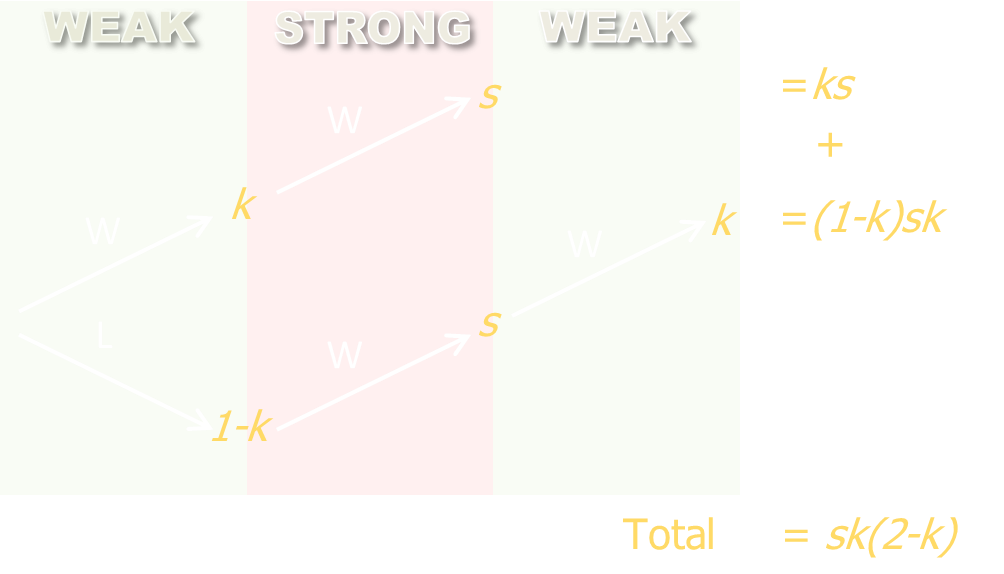
The total chance of victory for weak-strong-weak = ks + (1-k)sk = sk(2-k)
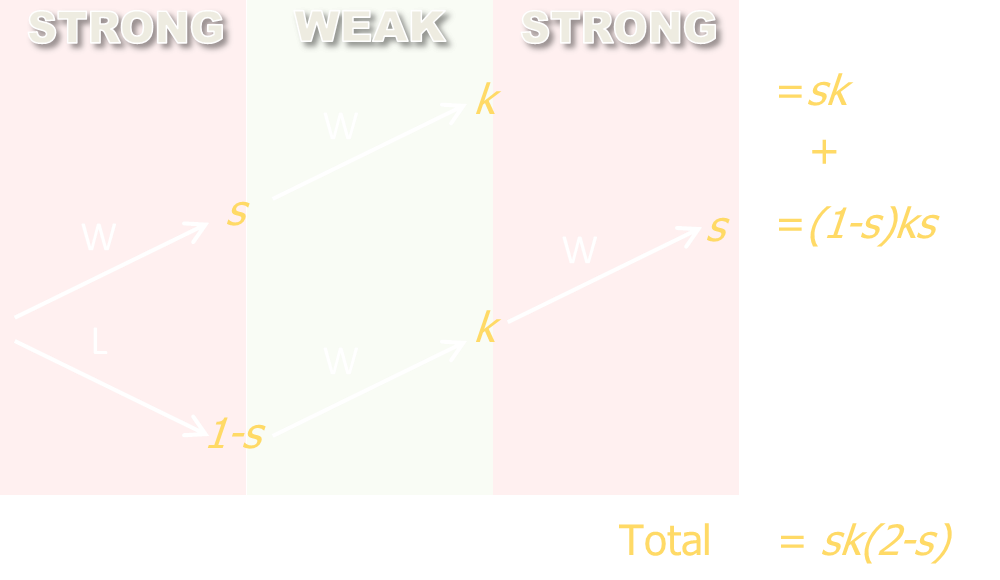
Strong-Weak-Strong
Similarly, for strong-weak-strong, the probability of winning is sk(2-s)
Result
Because k > s, it’s clear that sk(2-s) > sk(2-k), proving that strong-weak-strong is the way to go.
Putting in figures for our example s = 0.30 and k = 0.75, then:
Pr(Victory: weak-strong-weak) = 0.3 × 0.75 × (2 – 0.75) = 0.28125
Pr(Victory: strong-weak-strong) = 0.3 × 0.75 × (2 – 0.3) = 0.3825
If we play the strong player twice, the chance of winning two games in a row is 38.25%. If we play the weak player twice, our chance reduces to 28.125%.
That’s quite a difference.

Expected Number of Won Games
As mentioned above, this is a counter intuitive result. At first blush it seems illogical. The key is that victory conditions are two games in a row. In fact, if we look at the number of expected games we’d win using the optimal strategy we can see that, on average, we’ll lose more games by playing this way (even though we increase our overall chances of winning). It pays to always understand the rules before you play!
Here is a table of the expected number of wins, for each strategy, in the tournament. As you can see, the expected number of wins for playing weak-strong-weak is 2k+s, and the expected number of wins for strong-weak-strong is 2s+k
| Result | strong-weak-strongEXPECTED WINS | weak-strong-weakEXPECTED WINS | |
|---|---|---|---|
| win-win-win | 3sks | 3ksk | |
| win-win-loss | 2sk(1-s) | 2ks(1-k) | |
| win-loss-win | 2s(1-k)s | 2k(1-s)k | |
| win-loss-loss | s(1-k)(1-s) | k(1-s)(1-k) | |
| loss-win-win | 2(1-s)ks | 2(1-k)sk | |
| loss-win-los | (1-s)k(1-s) | (1-k)s(1-k) | |
| loss-loss-win | (1-s)(1-k)s | (1-k)(1-s)k | |
| loss-loss-loss | 0 | 0 | Total | 2s+k | 2k+s |
Plugging in our figures. If you play strong-weak-strong, the expected number of games you’d win in the tournament is just 1.3
If you play weak-strong-weak, the expected number of games you’d win is 1.8
